Если , то называется бинарным отношением на множестве . Основу для классификации таких отношений составляют следующие пять классов отношений.
Бинарное отношение 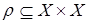 называется:
называется:
1) рефлексивным, если
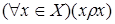 ;
;
2) антирефлексивным,
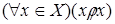 ;
;
3) симметричным, если
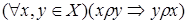 ;
;
антисимметричным, если
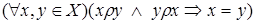 ;
;
5) транзитивным, если
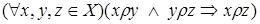 .
.
Замечание 2.3. Графическое изображение дает возможность следующим образом охарактеризовать в единых терминах первые четыре из определенных выше пяти классов бинарных отношений на множестве 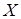 . Множество
. Множество 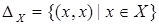 называется диагональю множества
называется диагональю множества 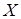 . Таким образом, отношение
. Таким образом, отношение 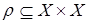 : 1) рефлексивно, если
: 1) рефлексивно, если  содержит диагональ
содержит диагональ 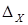 ; 2) антирефлексивно, если
; 2) антирефлексивно, если  не содержит ни одного элемента диагонали
не содержит ни одного элемента диагонали 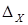 ; 3) симметрично, если графическое изображение
; 3) симметрично, если графическое изображение  симметрично относительно диагонали
симметрично относительно диагонали 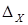 ; 4) антисимметрично, если при графическом изображении
; 4) антисимметрично, если при графическом изображении  , никакая его часть, лежащая вне диагонали
, никакая его часть, лежащая вне диагонали 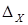 , не симметрична относительно диагонали
, не симметрична относительно диагонали 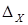 (отсюда, в частности, вытекает, что любое подмножество диагонали
(отсюда, в частности, вытекает, что любое подмножество диагонали 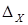 – антисимметричное отношение). Графическое изображение отношений, принадлежащих первым четырем, из определенных выше пяти классов бинарных
– антисимметричное отношение). Графическое изображение отношений, принадлежащих первым четырем, из определенных выше пяти классов бинарных
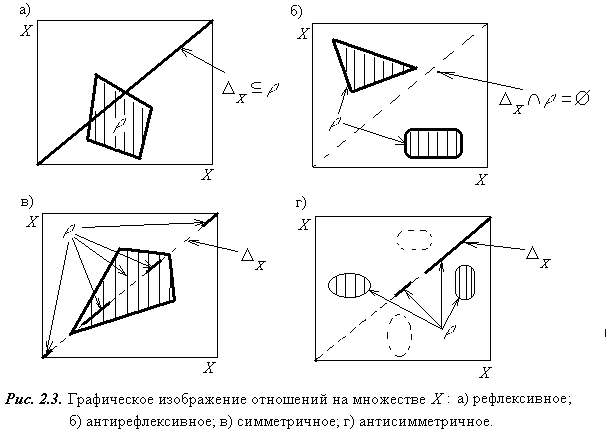 |
отношений на множестве
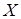 , показано на рис. 2.3.
, показано на рис. 2.3.
Пример 2.6. Рассмотрим отношения 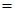 ,
, 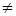 ,
, 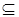 ,
, 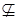 и
и 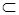 на множестве
на множестве 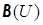 .
.
Из (1.1)-(1.3) вытекает, что отношение = рефлексивно, симметрично (и, в то же время, антисимметрично) и транзитивно, а отношение 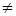 антирефлексивно и симметрично. Из (1.5)-(1.7) вытекает, что отношение
антирефлексивно и симметрично. Из (1.5)-(1.7) вытекает, что отношение 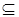 рефлексивно, антисимметрично и транзитивно, а отношение
рефлексивно, антисимметрично и транзитивно, а отношение 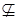 антирефлексивно. Из (1.11) и (1.13) вытекает, что отношение
антирефлексивно. Из (1.11) и (1.13) вытекает, что отношение 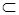 антирефлексивно и транзитивно. А так как
антирефлексивно и транзитивно. А так как
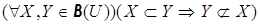 ,
,
то отношение 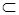 антисимметрично.
антисимметрично.
Выделим теперь следующие важные (с позиции, как самой математики, так и ее многочисленных приложений) классы бинарных отношений на множестве 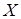 . Бинарное отношение
. Бинарное отношение 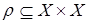 называется:
называется:
отношением эквивалентности (или эквивалентностью на множестве 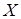 ), если
), если  рефлексивно, симметрично и транзитивно;
рефлексивно, симметрично и транзитивно;
отношением порядка (или порядком на множестве 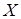 ), если
), если  рефлексивно, антисимметрично и транзитивно;
рефлексивно, антисимметрично и транзитивно;
отношением строгого порядка (или строгим порядком на множестве 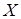 ), если
), если  антирефлексивно, антисимметрично и транзитивно;
антирефлексивно, антисимметрично и транзитивно;
отношением толерантности (или толерантностью на множестве 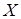 ), если
), если  рефлексивно и симметрично.
рефлексивно и симметрично.
Замечание 2.4. Антирефлексивное антисимметричное отношение 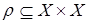 называется асимметричным отношением на множестве
называется асимметричным отношением на множестве 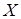 . Таким образом,
. Таким образом,  – отношение строгого порядка на множестве
– отношение строгого порядка на множестве 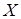 , если
, если  асимметрично и транзитивно.
асимметрично и транзитивно.
Замечание 2.5. Понятие отношение толерантности – это математический формализм, предназначенный для представления интуитивного понятия схожесть или близость (объектов, понятий, свойств и т.д.). Его значение характеризуется следующим образом. Пусть 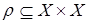 – отношение толерантности и
– отношение толерантности и 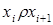
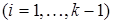 . Тогда последовательность
. Тогда последовательность 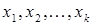 представляет последовательный, шаг за шагом, переход от объекта
представляет последовательный, шаг за шагом, переход от объекта 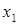 к объекту
к объекту 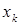 , причем на каждом шаге переход осуществляется от одного объекта к близкому к нему объекту.
, причем на каждом шаге переход осуществляется от одного объекта к близкому к нему объекту.

Определенные выше классы бинарных отношений на множестве 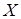 схематически представлены на рис. 2.4.
схематически представлены на рис. 2.4.
Пример 2.7. 1. Из свойств, установленных в примере 2.6, вытекает, что на множестве 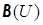 отношение
отношение 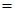 – эквивалентность, отношение
– эквивалентность, отношение 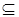 – порядок, а отношение
– порядок, а отношение 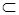 – строгий порядок.
– строгий порядок.
2. Определим бинарное отношение 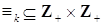 (
( 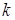 – фиксированное натуральное число) равенством
– фиксированное натуральное число) равенством
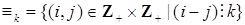 .
.
Дата добавления: 2015-10-09; просмотров: 1371;
