Вимірювання фізичних величин

Наука починається з тих пір,

коли починають вимірювати.

Точна наука немислима без вимірювань.

Д.І.Менделєєв

Вимірювання фізичних величин, які здійснюються в лабораторному практикумі, мають, в основному, пізнавальну мету. У лекційному курсі студенти вивчають теорію. При цьому розглядаються ті сторони реального світу, які існуюча теорія вважає найважливішими. Може трапитись так, що знайомство студентів з світом природи обмежиться лише цими сторонами, і вони будуть глибоко впевнені, що це і є весь реальний світ, а не його окремі сторони. До того ж в теорії все досить гармонійно пов’язане і дуже легко втратити уявлення, якими неймовірними зусиллями людського розуму вона створена. Займаючись лабораторним практикумом, студенти насамперед дізнаються, як важко буває перевірити теорію, і навчаться переборювати труднощі, які виникають при цьому, але крім всього іншого у них з’явиться погляд на фізику в цілому, на взаємозв’язок між теорією і експериментом, що складає головний зміст фізики як навчального предмета.

Фізичною величиною називають властивість, яка якісно є спільною для багатьох фізичних об’єктів, але кількісно різною для кожного з них. Кожна з фізичних величин описує якусь одну характеристику фізичного об’єкту. Наприклад, властивості об’єктів: довжина, маса, електричний опір; стани систем: тиск, температура, магнітна індукція; процеси: швидкість, прискорення, робота, потужність і т. д.

У пізнанні навколишнього світу важливе значення мають кількісні оцінки фізичних величин, які дають можливість відкрити діючі в природі закономірності, врахувати матеріальні ресурси, визначити якість різноманітної продукції і т. п. Серед різноманітних оцінок фізичних величин особливе місце займають фізичні вимірювання.

Вимірюванням називається порівняння вимірюваної величини з деяким її значенням, прийнятим за одиницю вимірювання. Результат фізичного вимірювання записують у вигляді такого рівняння:

Q = n [ Q ](1)

де n – числове значення фізичної величини Q; [ Q ] – її одиниця вимірювання.

Сукупність одиниць вимірювання фізичних величин, що охоплює певні галузі вимірювань, називається системою одиниць.

Кожна система одиниць фізичних величин складається з основних та похідних одиниць. Основною одиницею системи одиниць називається одиниця, яка прийнята за незалежну і використовується для визначення інших одиниць системи. Похідною одиницею системи називається одиниця, яка визначається через основні одиниці. Більшість похідних одиниць визначають із найпростіших рівнянь зв’язку між фізичними величинами.

Однією з важливих характеристик фізичної величини є її розмірність.

Розмірністю фізичної величини називають вираз, який показує зв’язок одиниці вимірювання цієї величини з основними одиницями даної системи одиниць. Цей вираз є одночленом у вигляді добутку символів основних одиниць у відповідних степенях (цілих або дробових, додатних або від’ємних). Наприклад, розмірність сили в системі СІ записується в такому вигляді:

[ F ] = L M T^-2,

де L – довжина; М – маса; Т – час.

Фізична величина називається безрозмірною, якщо у виразі її розмірності всі основні одиниці входять у нульовому степені.

Відносно сигналів вимірювальної інформації фізичні величини поділяються на активні і пасивні. Активними називаються фізичні величини, які можуть бути перетворені у сигнал вимірювальної інформації без використання допоміжних джерел енергії. Такими величинами є, наприклад, сила струму, напруга, температура, тиск і т. д. До пасивних величин, наприклад, належать електричний опір, індуктивність, маса і т. д.

Вимірювання відіграють важливу роль у житті людини. Без вимірювань неможливо уявити існування сучасної науки, промисловості, сільського господарства, медицини, торгівлі. Вимірювання необхідні в побуті, спорті та багатьох інших галузях діяльності людей. Сьогодні вони виконуються всюди: в земних умовах, в атмосфері, в космосі, на інших планетах. Вимірювання дозволяють керувати технологічними процесами, підприємствами, народним господарством у цілому. Вимірювальна інформація стала постійним супутником людини.

З розширенням сфери людської діяльності вимірювання охоплюють все нові фізичні величини, істотно розширюються діапазони вимірювань. Так, наприклад, діапазон вимірювання довжини складає від 20-100 нм до мільйонів кілометрів, температури — від 0.5К до кількох мільйонів кельвінів, тиску — від 1·10^-10 Па до 0.4·10¹⁰ Па, електричного опору — від 10^-6 Ом до 10¹⁷ Ом, індуктивності — від 10^-8 Гн до 10⁴ Гн, електроємності — від 10^-15 Ф до 10 Ф, потужності — від 10^-15 Вт до 10⁹ Вт, сили струму від 10^-16 А до сотень ампер.

Сьогодні є необхідність вимірювати понад 2000 різних фізичних величин. Існуючі нині методи і засоби дають можливість вимірювати лише близько 800 величин. Отже, є постійна проблема розробляти і освоювати нові методи вимірювань та конструювати та виготовляти нові вимірювальні прилади.

Різко зросли і продовжують зростати вимоги до точності вимірювань, швидкості одержання вимірювальної інформації, якості вимірювань фізичних величин, особливо тих, які характеризують швидкопротікаючі процеси. Автоматизація виробництва та впровадження гнучких виробничих ліній обумовлюють необхідність повної автоматизації вимірювань, використання систем автоматичного контролю, безконтактних методів вимірювань, вимірювальних роботів.

Аналіз тенденцій розвитку науки і техніки дає можливість зробити висновок про необхідність дальшого підвищення точності вимірювань малих і середніх довжин у машинобудуванні, товщини тонких і надтонких плівок і покриттів у мікро- і оптоелектроніці, об’ємів корисних копалин при геологічній розвідці, витрати сировини у добувних і переробних галузях промисловості і т. д.

У залежності від способів одержання результатів фізичні вимірювання поділяють на прямі, посередні, сукупні та сумісні.

Прямими називають вимірювання, при яких певна фізична величина безпосередньо порівнюється з одиницею вимірювання або за допомогою вимірювального приладу, проградуйованого у відповідних одиницях. До прямих вимірювань відносяться вимірювання довжини масштабною лінійкою, штангенциркулем, плитками Йогансона і т. д. ; вимірювання маси на терезах за допомогою різноважок; вимірювання проміжків часу за допомогою годинника або секундоміра; вимірювання температури за допомогою термометра, сили струму за допомогою амперметра і т. д.

Посередніми називаються вимірювання, при яких шукане значення фізичної величини знаходять на підставі відомої залежності між цією величиною і величинами, які можна вимірювати безпосередньо. Прикладами посередніх вимірювань можуть служити вимірювання швидкості рівномірного (або рівноприскореного) руху на підставі прямих вимірювань пройденого шляху і проміжку часу; вимірювання густини тіла і т. д.

Сукупними називають вимірювання, при яких одночасно вимірюється декілька однойменних величин, а шукану величину визначають шляхом розв’язку системи рівнянь, одержаних при прямих вимірюваннях різних сполучень цих величин.

Сумісними називаються вимірювання, при яких одночасно вимірюються дві або декілька не однойменних величин для знаходження залежності між ними. Сумісними вимірюваннями, наприклад, є дослідження залежності опору провідників або напівпровідників від температури, вимірювання коефіцієнта лінійного ослаблення g -променів і т. д.

При аналізі вимірювань слід чітко розрізняти істинні значення фізичних величин і їх емпіричні прояви — результати вимірювань.

Істинним значенням фізичної величини називається значення, яке ідеально в якісному і кількісному відношенні відображає відповідну властивість об’єкта. Воно не залежить від засобів нашого пізнання і є тією абсолютно істиною, до якої ми прагнемо.

Результати вимірювань, навпаки, є продуктами нашого пізнання. Це наближені оцінки фізичних величин, знайдені шляхом спостережень. Вони залежать не тільки від самих величин, але ще й від методів вимірювання, від технічних засобів, за допомогою яких проведені вимірювання, і від властивостей органів відчуття експериментатора, який здійснює вимірювання.

Значення фізичної величини, одержане в результаті вимірювання називається дійсним значенням. Вважають, що дійсне значення настільки близьке до істинного, що може його замінити.

Таким чином, через недосконалість засобів вимірювання і органів відчуття експериментатора, а також через багато численні збурення результат вимірювання фізичної величини х, як правило, відрізняється від його істинного значення х₀, тобто має похибку.

Похибкою вимірювання називають відхилення результату вимірювання від істинного значення вимірюваної величини. Розрізняють абсолютну та відносну похибки.

Похибка:Dх= x - x₀,(2)

яка виражена в одиницях вимірюваної величини, називається абсолютною похибкою, а похибка:

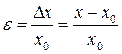(3)

яка виражена в частинах або процентах від істинного значення вимірюваної величини, називається відносною похибкою.

Оскільки істинне значення х₀вимірюваної величини невідоме, то невідомі і похибки вимірювання Dх і e.Щоб отримати хоча б наближені результати, доводиться замість істинного значення фізичної величини підставляти його дійсне значення.

У залежності від закономірності появи похибки вимірювань поділяють на три типи: грубі, систематичні і випадкові.

Грубою похибкою або промахом називають похибку вимірювання, яка суттєво перевищує очікувану при даних умовах вимірювання.

Систематичною похибкою називають похибку вимірювання, яка залишається постійною або закономірно змінюється при повторних вимірюваннях однієї і тієї ж величини. Систематичні похибки часто виникають через те, що умови експерименту відрізняються від передбачуваних теорією, а поправки на цю невідповідність не зроблено.

Найбільш поширеним джерелом систематичних похибок є похибки вимірювальної апаратури.

Випадковою похибкою називається похибка, яка змінюється випадково при повторних вимірюваннях однієї і тієї ж фізичної величини. Випадкові похибки можна виявити шляхом повторних вимірювань. Крім того, збільшуючи число вимірювань і знаходячи середнє арифметичне їх результатів, ми будемо отримувати дійсні значення, які будуть наближатися до істинного значення. Але при наявності систематичної похибки це нічого не дасть. Повторні вимірювання за допомогою одного і того ж приладу не дають можливості ні виявити, ні усунути систематичні похибки. Тому систематичні похибки більш небезпечні, ніж випадкові. Якщо в ході експерименту допущені великі випадкові похибки, то вони виявлять себе у великій величині похибки кінцевого результату. Таким чином, всі будуть освідомленні про неточність результату і це не завдасть нікому ніякої шкоди, хіба що тільки самолюбству експериментатора, оскільки одержаний ним результат ні на кого не справить приємного враження. Інша справа, коли при наявності прихованої систематичної похибки результат буде виглядати цілком надійним, якщо він наведений з малою похибкою, хоча насправді він неправильний. Класичним прикладом цього може служити дослід Міллікена з вимірювання елементарного електричного заряду. У цьому експерименті потрібно знати в’язкість повітря. Відоме на той час значення коефіцієнта в'язкості повітря виявилось заниженим. Тому Міллікен одержав результат:

е=1,591 ± 0,002·10^-19 Кл

Сьогодні для цієї величини приймають значення:

е= ( 1,60217733 ± 0,00000049)·10^-19 Кл

Аж до 1930 р. включно, числові значення ряду інших атомних констант, таких, як стала Планка і число Авогадро, базувались на міллікенівському значенні e , отже, містили систематичну похибку, більшу за 0,5%.

Закономірності випадкових похибок детально вивчені і розроблені методи їх оцінок. Поява тієї чи іншої випадкової похибки є так званою випадковою подією. Випадковими подіями називають такі події, поява яких не може бути точно передбаченою. Вони вивчаються теорією імовірностей, яка дає методи розрахунку імовірності їх появи.

Вимірювання, які виконуються при додаткових умовах, одним і тим же дослідником, одним і тим же приладом, за тією ж самою методикою вимірювань, називаються рівно точними. Нехай при повторних рівно точних вимірюваннях деякої фізичної величини x одержали n числових значень, які дещо відрізняються одне від одного:

х₁, х₂, х₃, ... х_n.

Припустимо, що в цьому ряді немає систематичних і грубих похибок. Тоді відхилення кожного з цих результатів вимірювання від істинного значення і вимірюваної величини можна вважати випадковою похибкою цього вимірювання:

Dx_i = x_i – x₀.

Різні за числовим значенням похибки мають різну імовірність своєї появи. У більшості фізичних вимірювань випадкові похибки описуються так званим законом нормального розподілу або формулою Гаусса. Ця формула одержана з врахуванням таких емпіричних положень:

1) імовірність появи похибки зменшується із збільшенням її числового значення, тобто чим більша абсолютна величина похибки, тим рідше вона зустрічається;

2) при великому числі вимірювань похибки однакової абсолютної величини, але різних знаків, мають однакову імовірність.

Формула Гаусса має такий вигляд:

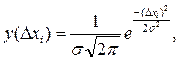(5)

де y(Dx_i)–імовірність появи похибки Dx_i;

e – основа натуральних логарифмів;

s–середнє квадратичне відхилення результату спостереження;

Dx_i = x_i - x₀ ;

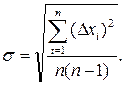(6)

Графіки формули Гаусса для деяких значень s показані на рис.1.

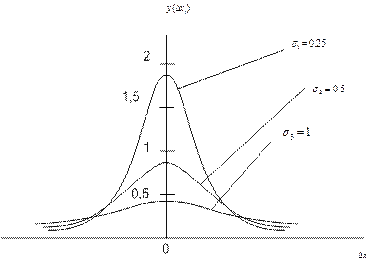
Рис. 1.

3 цього рисунка видно, що чим менше s, тим менша імовірність появи великої за абсолютною величиною випадкової похибки Dx_i.

Середнє квадратичне відхилення s результату спостереження характеризує розкид окремих значень x_i даного ряду результатів вимірювання. Чим менше s, тим менший розкид окремих значень x_i, тобто вища точність вимірювань.

Користуючись кривою нормального розподілу випадкових похибок (рис. 1), легко визначити імовірність появи відхилень певного числового значення. Але ще більший інтерес становить визначення імовірності того, що відхилення Dx_i лежать в межах -Dxдо Dx, тобто імовірність появи відхилень Dx_i, абсолютна величина яких не перевищує деякого заданого значення ½Dx½. Цю імовірність називають довірчою імовірністю і позначають буквою p.

Інтервал значень від x₀ - Dxдо x₀ + Dx, в який попадає дійсне значення вимірюваної величини із заданою імовірністю pназивають довірчим інтервалом. Зрозуміло, що чим більшої довірчої імовірності ми вимагаємо, тим більшим буде відповідний довірчий інтервал, і, навпаки, чим більший довірчий інтервал ми задаємо, тим імовірніше, що результати вимірювань не вийдуть за його межі.

При виконанні лабораторних робіт рекомендується вибирати довірчу імовірність p=0,9. При обмеженій кількості вимірювань (n= 5...10) вводять коефіцієнт Стьюдента t_p,n ,який залежить від числа вимірювань n_і і довірчої імовірності. Значення коефіцієнтів Стьюдента для різних значень n при довірчій імовірності p=0,9 наведені в табл.1.

Таблиця 1

Похибки прямих вимірювань

Припустимо, що грубі похибки відсутні, а систематичні похибки вилучені, тобто неточність вимірювання визначається тільки похибкою вимірювальних приладів і випадковими похибками. Можливі три випадки:

1) випадкові похибки менші за похибки приладу;

2) випадкові похибки такого ж порядку, як похибки приладу;

3) випадкові похибки більші за похибки приладу.

У першому випадку похибка вимірювання оцінюється тільки за похибкою приладу, а в другому випадку похибка вимірювання розраховується за формулами, які дає теорія випадкових похибок.

Для з'ясування, який випадок має місце, необхідно виконати декілька однакових вимірювань. Якщо результати всіх вимірювань однакові в межах похибки приладу, то похибка вимірювання визначається похибкою приладу (систематична похибка вимірювання):

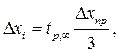(7)

де t_p,¥ – коефіцієнт Стьюдента при n ® ¥,

Dx_np – абсолютна похибка приладу.

Абсолютна похибка приладу, як правило дорівнює половині ціни його поділки або визначається класом його точності (найчастіше для електровимірювальних приладів).

У другому випадку проводятьn рівноточних вимірювань. Теорія випадкових похибок доводить, що найбільш близьким до істинного значення вимірюваної величини є середнє арифметичне ряду рівно точних вимірювань, тобто

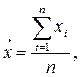(8)

де x_i – числове значення, одержане при і-му вимірюванні.

Оскільки відхилення результату вимірювання Dx від істинного значення вимірюваної величини (4) нам невідоме (внаслідок невизначеності x₀), то відповідно нам невідома і величина s , яка визначається формулою (6). Тому вводять величину

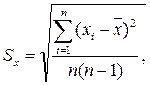(9)

яку називають оцінкою середнього квадратичного відхилення результатів вимірювання від їх середнього арифметичного.

Якщо вимірювань дуже багато, то виконується співвідношення:

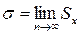
Випадкова абсолютна похибка визначається за формулою:

Dx₂ = t_p,n S_x, (10)

де t_p,n –коефіцієнт Стьюдента.

Загальна абсолютна похибка вимірювання у цьому випадку дорівнює:

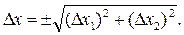(11)

У третьому випадку, очевидно, абсолютна похибка вимірювання визначається за формулою (10).

Остаточні записи результату прямого вимірювання мають форму:

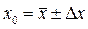
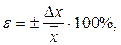(12)

де E – відносна похибка вимірювання.

Запис результату вимірювання

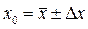
означає, що істинне значення x₀ вимірюваної величини з імовірністю pлежить в середині інтервалу [ , ].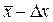

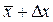Таким чином, можна рекомендувати слідуючий порядок математичної обробки результатів прямих вимірювань:

1) знайти абсолютну систематичну похибку вимірювання, користуючись формулою (7);

2) знайти середнє арифметичне значення вимірюваної величини за формулою (8);

3) знайти оцінку середнього квадратичного відхилення за формулою (9);

4) знайти абсолютну випадкову похибку, користуючись табл. 1 і формулою (10);

5) знайти загальну абсолютну похибку вимірювання за формулою (11);

6) записати остаточний результат (12).

Похибки посередніх вимірювань

Нехай вимірюється деяка фізична величина y, яка є функцією незалежних величин х₁, х₂ ,..., х_n, числові значення яких знаходять за допомогою прямих вимірювань:

y = f(х₁, х₂ ,..., х_n),(13)

Необхідно знайти похибки вимірювання величини y за відомими похибками незалежних змінних x_i, i = 1, … ,n.

Абсолютну похибку вимірювання величини y можна знайти за формулою:

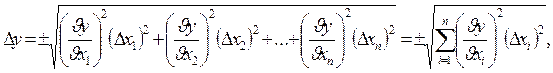(14)

де Dx_i – загальні абсолютні похибки прямих вимірювань величин x₁, x₂,x₃, ...,x_n, знайдених за правилами, розглянутими у попередньому розділі.

Середнє значення y отримується підстановкою в (13) середніх арифметичних x₁, x₂, ... , х_n. Значення частинних похідних у формулі (14) знаходяться для середніх арифметичних значень величин x₁, x₂, ... , x_n.

Для математичної обробки результатів посередніх вимірювань можна рекомендувати слідуючий порядок:

1) виміряти кілька разів величини x₁, x₂, ... , x_n(але не менше 3 вимірювань кожної з них);

2) виконати п.п. 1-6 попереднього розділу;

3) визначити середнє значення досліджуваної величини y за формулою:

y = f ( x₁, x₂, ... , x_n);

4) знайти абсолютну похибку вимірювання величини y за формулою (14);

5) записати одержані результати в такому вигляді:

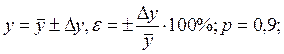
6) зробити аналіз одержаних результатів та висновки.

При математичній обробці результатів вимірювання доводиться використовувати табличні дані математичних та фізичних величин. Ці дані наводяться з правильними цифрами і однією (останньою) сумнівною. За абсолютну похибку табличних величин приймають половину одиниці сумнівної цифри. Наприклад, sin 58°= 0,8480.

Абсолютна похибка дорівнює ±0,00005.

У фізичному лабораторному практикумі є лабораторні роботи, в яких тачи інша фізична величина отримується шляхом сумісних вимірювань. Наприклад, вимірювання термічного коефіцієнту опору, сталої термо-е.р.с. Теорія випадкових похибок рекомендує в цьому випадку використовувати так званий метод найменших квадратів.

Слід звернути увагу, що в останні роки набули поширення нестатистичні методи математичної обробки результатів вимірювань. Одним з них є метод, який базується на понятті нечітких (розмитих) множин. Теорія нечітких множин за свої 25 років існування перетворилась у розвинуту теорію, яка має важливе практичне застосування в тих випадках, коли задачі не допускають точного формулювання, включаючи неточності і невизначеності.

Розділ перший

Механіка

Перед початком виконання лабораторної роботи студенту необхідно одержати допуск до роботи. Для цього йому слід відповісти на декілька запитань з теорії методу і знання лабораторної установки. Одержавши відмітку про допуск на бланку звіту, студент може приступити до виконання роботи.

Проробивши всі необхідні вимірювання і записавши їх в звіт студент виконує контрольні розрахунки, тобто знаходить одну або декілька вимірюваних величин і при необхідності узгоджує їх у викладача. Бланк звіту з результатами контрольного розрахунку підписується у викладача.

В першому розділі перед початком подання теорії методу до кожної лабораторної роботи є посилання на підручники, які в достатній кількості є в науковій бібліотеці університету.

1. Савельєв И.В. "Курс общей физики". Т.І.М:Наука:1977.

2. Яворский Б.М. і.інш. "Курс физики". Т.І.М:Наука:1977.

Студент може користуватись також будь-яким іншим підручником де є відповідний теоретичний матеріал.

Лабораторна робота № 1-1

Дослідження прямолінійного руху тіл в полі

тяжіння за допомогою машини Атвуда.

Л. 1. §§ 3, 4, 7, 8.

Мета роботи: дослідити закони руху тіл в полі земного тяжіння.

Прилади і матеріали: машина Атвуда, набір важків, додаткові

тягарці, електронний секундомір.

Теоретичні відомості.

Машина Атвуда призначена для вивчення законів прямолінійного рівномірного та рівномірно прискореного рухів і, зокрема, для визначення прискорення вільного падіння тіл.

Будова машини Атвуда зображена на рис.1. Принцип її дії грунтується на використанні законів вільного падіння тіл в повітрі. Через нерухомий блок, при обертанні якого силою тертя в осі можна знехтувати, перекинута нитка з двома однаковими вантажами масою М кожний. В цьому випадку система знаходиться в рівновазі. Якщо на один з вантажів покласти невеликий додатковий тягарець масою m, то система, що складається з двох вантажів і тягарця, одержить деяке прискорення a під дією сили F= mg і на шляху S₁ , буде рухатись з цим прискоренням.

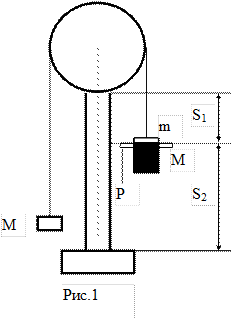
Кільцем Рдія додаткового тягарця m припиняється і вантажі, рухаючись рівномірно, пройдуть шляхS₂.

Знайдемо закон руху вантажу М , розташованого праворуч. Для цього скористаємося системою координат, початок якої знаходиться на осі блока, а вісь ox напрямлена вертикально вниз. На вантаж Мдіють дві сили : сила тяжіння (М+m)g та сила натягу правої частини нитки Т₁. Запишемо другий закон Ньютона:

( М + m ) g - T₁ = ( M + m ) a ,(1)

де а – прискорення вантажу М.

Тепер застосуємо другий закон Ньютона до вантажу М, що розташований ліворуч. Так як нитка нерозтяжна, прискорення лівого вантажу за абсолютним значенням рівне прискоренню правого, але направлене в протилежний бік, тобто воно рівне – а. Натяг лівого кінця нитки позначимо через Т₂ , тоді :

М g - T₂ = - M а,(2)

У випадку невагомого блока і відсутності сили тертя в його осі :

Т₁ = Т₂ . (3)

З рівнянь ( 1 ),( 2 ) та ( 3 )знайдемо прискорення системи :

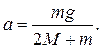(4)

Таким чином, вважаючи g відомим та проводячи досліди з різними вантажами Мі додатковими тягарцями m,за формулою (4)можна вирахувати прискорення а і здійснити експериментальну перевірку другого закону Ньютона.

Машина Атвуда дає можливість також визначити прискорення вільного падіння g, що й складає основне завдання даної роботи. Для цього з формули (4)знайдемо g:

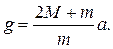(5)

Прискорення абезпосередньо виміряти неможливо, але його легко вирахувати, вимірявши шлях S₁ , пройдений вантажем Мпри рівномірно прискореному русі, а також шлях S₂ рівномірного руху та час tйого проходження.

Для рівномірно прискореного руху, при умові, що початкова швидкість V₀рівна нулеві, пройдений шлях можна знайти, маючи кінцеву швидкість та прискорення :

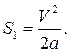(6)

Кінцева швидкість V набувається вантажем Мв момент проходження кільця Р, яке припиняє дію додаткового тягарця. Далі з цією швидкістю вантаж рухається рівномірно і за час t проходить шлях S₂ . Тому :

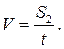(7)

З формул (6) і (7)знаходимо прискорення а, підставляючи його значення в вираз(5),остаточно одержуємо :

(8)

де М– маса великого вантажу;

M– маса додаткового тягарця;

S₁– шлях, що проходить вантаж (М+m)при рівномірно прискореному русі;

S₂– шлях, пройдений вантажем Мпри рівномірному русі;

T–час проходження шляху S₂.