При заданной мощности нагрузки
Задано напряжение в конце линии 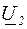 = const. Известны (рис. 3.3) мощность нагрузки
= const. Известны (рис. 3.3) мощность нагрузки 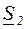 , напряжение
, напряжение 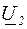 , сопротивление и проводимость линии
, сопротивление и проводимость линии 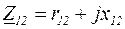 ,
, 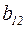 . Определим напряжение
. Определим напряжение 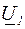 , мощности в конце и в начале продольной части линии
, мощности в конце и в начале продольной части линии 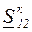 ,
, 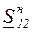 , потери мощности
, потери мощности 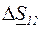 , мощность в начале линии
, мощность в начале линии 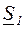 . Для проверки по нагреву иногда определяют ток в линии
. Для проверки по нагреву иногда определяют ток в линии 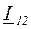 .
.
 Рис.3.3 Схема замещения линии для расчета
Рис.3.3 Схема замещения линии для расчета
при заданной мощности нагрузки
Расчет аналогичен расчету, приведенному в п.3.1, и состоит в последовательном определении от конца линии к началу неизвестных мощностей и напряжений при использовании первого закона Кирхгофа и закона Ома. При выводе формул будем использовать мощности трех фаз и линейные напряжения. Зарядная (емкостная) мощность трех фаз в конце линии
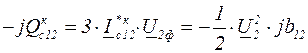 . (3.9)
. (3.9)
Мощность в конце продольной части линии по первому закону Кирхгофа
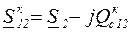 . (3.10)
. (3.10)
Потери мощности в линии равны
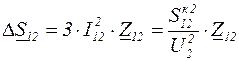 . (3.11)
. (3.11)
Ток в начале и в конце продольной ветви линии одинаков.
Мощность в начале продольной ветви линии больше, чем мощность в конце, на величину потерь мощности в линии, т.е.
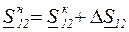 . (3.12)
. (3.12)
Линейное напряжение в начале линии по закону Ома равно
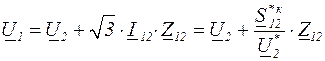 . (3.13)
. (3.13)
Емкостная мощность в начале линии
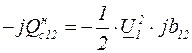 . (3.14)
. (3.14)
Мощность в начале линии
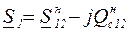 . (3.15)
. (3.15)
Дата добавления: 2015-10-09; просмотров: 799;
