Падение и потеря напряжения в линии

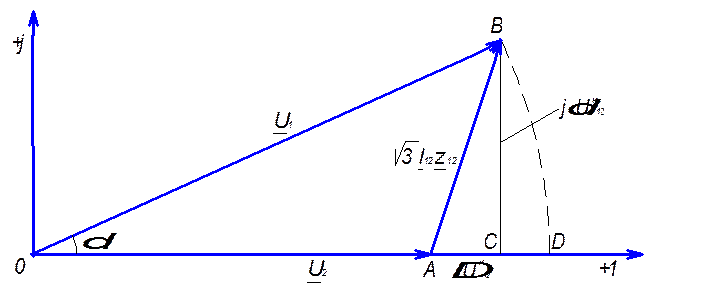
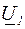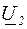На рис.3.4 приведена векторная диаграмма для линейных напряжений в начале и в конце линии и . Эта диаграмма аналогична диаграмме на рис.3.2,а.

Падение напряжения – геометрическая (векторная) разность между комплексами напряжений начала и конца линии. На рис.3.4 падение напряжения – это вектор 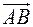, т.е.

.

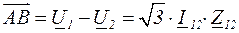Продольной составляющей падения напряжения 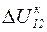называют проекцию падения напряжения на действительную ось или на напряжение 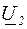, 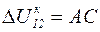на рис.3.4. Индекс «к» означает, что 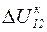- проекция на напряжение конца линии 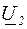. Обычно 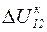выражается через данные в конце линии: , , .

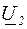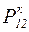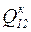Поперечная составляющая падения напряжения 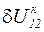- это проекция падения напряжения на мнимую ось, 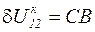на рис.3.4. Таким образом, падение напряжения

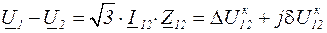. (3.16)

Часто используют понятие потеря напряжения – это алгебраическая разность между модулями напряжений начала и конца линии. На рис.3.4 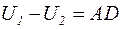. Если поперечная составляющая 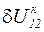мала (например, в сетях 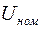≤ 110 кВ), то можно приближенно считать, что потеря напряжения равна продольной составляющей падения напряжения.

Рис.3.4 Векторная диаграмма напряжений

в начале и в конце линии при расчете по данным конца