Это и есть нетто-ставка с одного объекта страхования.
Долю участия каждого страхователя в формировании денежного фонда можно определить и с единицы страховой суммы (т.е. со 100 руб.), разделив сумму, необходимую для выплат, на общую страховую сумму (в нашем примере она совпадает со стоимостью) всех застрахованных домов.
1 800 000 руб./ (300 000 руб. ×1 000) ×100 = 0,6 руб. (со 100 руб.), или 0,6 %.
Полученный результат также есть нетто-ставка, но с единицы страховой суммы. То есть если страховую сумму (300 000 руб.) умножить на нетто-ставку (0,6 %), то получим сумму страховой премии, которую домовладелец должен заплатить:
300000 руб. × 0,6 / 100 = 1 800 руб.
На практике расчет нетто-ставки более сложен, т.к. требует учета степени повреждения застрахованных объектов (часть домов сгорает не полностью, а лишь частично), колебаний числа страховых случаев (например, пожаров, наводнений и т. д.) по годам и ряда других факторов. Вероятность гибели или повреждения разного имущества (зданий, животных, сельскохозяйственных посевов и т. д.) от всевозможных страховых событий (пожар, болезни, вымерзание и т. п.) весьма различна. Следовательно, должны быть различны и тарифные ставки, применяемые при страховании того или иного объекта от выбранного страхового риска.
Существует несколько методик расчета величины нетто-ставки:
Методика 1. Предположим, что страховщику необходимо рассчитать нетто-ставку по новому для него виду – страхованию автомобилей на случай повреждения в результате ДТП. Поскольку своей статистики у страховой организации нет, она может воспользоваться данными ДПС и авторемонтных мастерских.
Данные необходимы для расчета тарифной ставки:
Вернемся к показателю убыточности страховой суммы. Числитель дроби (сумма страховых выплат) можно представить как произведениесредней выплаты на один объект(СВ) и числа пострадавших объектов (n), а знаменатель (страховая сумма) – как произведение средней страховой суммы (СС) и числа застрахованных объектов (з). В результате получим:
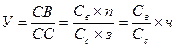
При этом в нашем примере средняя выплата на один объект есть средняя стоимость ремонта одного автомобиля, а отношение числа пострадавших объектов к общему числу застрахованных (ч) есть частота наступления ДТП, приведших к повреждению автомобилей.
Таким образом, если стоимость одного автомобиля равна 80 000 руб., стоимость ремонта – 20 000 руб., а частота ДТП – 0,2 (т.е., по данным ДПС, в аварию попадает каждая пятая машина), то убыточность страховой суммы составит:
У = 20000/80000 ×0,2 ×100 руб. = 5 руб., или 5 %.
Рисковая надбавка учитывает вероятное превышение числа страховых случаев (в нашем примере – числа поврежденных автомобилей) относительно их средней величины. Рисковая надбавка зависит от числа договоров, которые страховщик планирует заключить за год, и степени гарантии того, что собранных взносов хватит на страховые выплаты.
Если исходить из предположения, что выплаты не должны превысить страховую премию с гарантией:
84 % – коэффициент равен 1;
90 % – соответственно 1,3;
95 % – 1,645 и т.д.
В нашем примере при числе договоров 100 и степени гарантии 90 % рисковая надбавка будет равна:
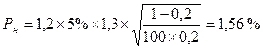
Сложив убыточность страховой суммы и рисковую надбавку, получим искомую величину нетто-ставки:
5 % + 1,56 %= 6,56 %
Методика 2. В том случае, когда страховщик имеет статистику за 3-5 лет, целесообразно использовать другую методику для расчета нетто-ставок – на основе показателей убыточности страховой суммы. Здесь определение нетто-тарифа осуществляется на базе страховой статистики за прошлые годы с учетом прогнозируемого уровня убыточности на следующий год. Для расчета прогнозной величины убыточности фактические данные выравниваются на основе линейного уравнения:
Ун 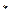 = Аа + Ав×н,
= Аа + Ав×н,
где Ун 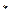 – выровненный показатель убыточности;
– выровненный показатель убыточности;
Аа, Ав – параметры уравнения;
н – порядковый номер соответствующего года.
Параметры уравнения Аа и Ав определяются методом наименьших квадратов на основе решения системы уравнений с двумя неизвестными.
Покажем решение данной системы на конкретном примере расчета нетто-ставки (табл. 3.1).
Таблица 3.1
Пример расчета нетто-ставки
| Годы | н | Факти-ческая убыточ-ность, Ун | Расчетные показатели | Выров-ненная убыточ-ность,
Ун 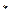
| Отклонения выровненной убыточности,
Ун 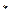 – Ун – Ун
| Квадраты отклонений,
(Ун 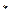 – Ун) – Ун) 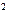
| |
| Ун × н | н | ||||||
| гр3×гр2 | гр.6-гр.3 | ||||||
| 0,18 | 0,18 | 0,192 | +0,012 | 0,000144 | |||
| 0,26 | 0,52 | 0,244 | -0,016 | 0,000256 | |||
| 0,29 | 0,87 | 0,296 | +0,006 | 0,000036 | |||
| 0,36 | 1,44 | 0,348 | -0,012 | 0,000144 | |||
| 0,39 | 1,95 | 0,400 | +0,010 | 0,000100 | |||
| сумма | 1,48 | 4,96 | 0,000680 |
Подставив полученные в табл. 3.1 данные в систему уравнений, имеем:
Аа×5+Ав×15=1,48;
Аа×15+Ав×55 = 4,96.
Решив эту систему уравнений, получаем Аа = 0,14, Ав = 0,052. Теперь можем определить ожидаемую убыточность на 2014 год.
У6 = Аа+Ав×6 = 0,14 + 0,052×6 = 0,452.
Подставляя необходимые данные в уравнение Ун  , рассчитаем выровненную убыточность, которая используется для определения рисковой надбавки как среднее квадратическое отклонение фактических значений убыточности от выровненных.
, рассчитаем выровненную убыточность, которая используется для определения рисковой надбавки как среднее квадратическое отклонение фактических значений убыточности от выровненных.
В табл. 3.1 в графах 6-8 приведены соответственно выровненная убыточность, отклонение выровненной убыточности от фактической и квадраты отклонений.
Для определения среднего квадратического отклонения применяется следующая формула:
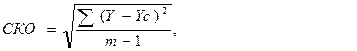 |
где
СКО – среднее квадратическое отклонение;
∑(Y – Yс) 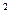 – сумма квадратов линейных отклонений;
– сумма квадратов линейных отклонений;
т – число лет, за которые используются данные для расчета.
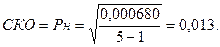 Подставив сумму квадратов отклонений в выше обозначенную формулу, получим:
Подставив сумму квадратов отклонений в выше обозначенную формулу, получим:
Нетто-ставка определяется как сумма ожидаемой убыточности и рисковой надбавки, скорректированной на определенный коэффициент.
Величина этого коэффициента зависит от степени предусматриваемой гарантии и числа анализируемых лет. Так, при гарантии 90% и пятилетнем ряде отчетных данных коэффициент равен 1,984.
В этом случае нетто-ставка составит:
0,452 + 0,013×1,984 = 0,48 руб., или 0,48 %.
Для определения окончательной брутто- ставки к нетто-ставке прибавляется нагрузка. После этого страховая премия (цена) может быть скорректирована за счет скидок и надбавок.
Дата добавления: 2015-10-09; просмотров: 1110;
