Применение дифференциала в приближенных вычислениях

Выше было показано, что 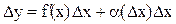, т.е. приращение функции Dу отличается от ее дифференциала dy на бесконечно малую величину более высокого порядка, чем Dх.

Поэтому при достаточно малых значениях Dх Dу » dy или
f(x + Dх) - f(x) » f `(x)Dх, откуда f(x + Dх) » f(x) + f `(x)Dх. Полученная формула будет тем точнее, чем меньше Dх.

Например, найдем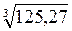

Итак, y = f(x) = x^1/3. Возьмем x = 125, Dх = 0,27.

f `(x) = (x<sup>1/3</sup>)`= 1/(3x^2/3)

f(125,27) = f(125 + 0,27) » f(125) + f `(125)*(0,27) = 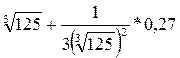= 5 + 0,27/(3*25) = 5,0036

Например, найдем tg 46^о.

Итак, y = f(x) = tg x. Возьмем x = 45^o = p/4, Dх = 1^o = p/180.

f `(x) = (tg x)`= 1/cos²x

f(46^o) = f(p/4 + p/180) » f(p/4) + f `(p/4)*(p/180) = tg(p/4) +
+ (1/ cos²(p/4))*(p/180) = 1 + (1/(Ö2/2)²)*(p/180) = 1 + p/90 (» 1,035)

Кроме того, с помощью дифференциала может быть решена задача определения абсолютной и относительной погрешностей функции по заданной погрешности нахождения (измерения) аргумента.

Пусть необходимо вычислить значение данной функции у = f(x) при некотором значении аргумента х₁, истинная величина которого неизвестна, а известно лишь его приближенное значение х с абсолютной погрешностью |Dх| = |х - х₁|. Если вместо истинного значения f(x₁) взять величину f(x), то абсолютная ошибка функции будет равна |f(x₁) - f(x)| = |Dy| » dy = f `(x)Dх.

При этом относительная погрешность функции d_y = |Dy/y| при достаточно малых Dх будет равна 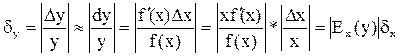, где Е_х(y) – эластичность функции, а d_х = |Dx/x| - относительная погрешность аргумента.