Теоретическое описание работы и вывод рабочей формулы

Маятник в процессе колебаний совершает поступательное и вращательное движения, которые описываются соответствующими уравнениями. Для составления уравнений движения рассмотрим силы и моменты сил, действующих на маховичок (рис. 1). Пусть 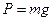- сила тяжести, 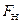- сила натяжения одной нити. 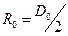- радиус оси маятника. 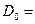10 мм - диаметр оси маятника, 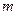- масса маятника. J- момент инерции маховичка. Тогда уравнение поступательного движения, согласно второму закону Ньютона, запишется так:

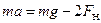. (1)

В уравнении (1) стоит удвоенное значение силы 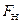, так как на ось маховичка намотаны две нити, в каждой из которых возникает сила натяжения .

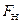Под действием сил натяжения диск совершает вращательное движение. Момент этих сил равен:

. (2)

Плечом силы 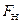является радиус 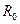оси маятника, диаметром нити пренебрегаем.

Тогда уравнение вращательного движения маховичка можно записать так:

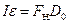, (3)

где 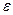- угловое ускорение вращения диска.

Угловое ускорение 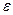и ускорение центра масс 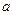связаны соотношением:

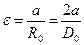. (4)

Ускорение 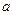, центра масс можно найти, зная длину пути и время движения маховичка от верхней до нижней точки (с учетом нулевой начальной скорости):

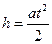. (5)

Откуда

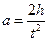. (6)

Подставив (6) в (4), получим:

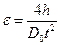. (7)

С учетом (6) и (7) уравнения (1) и (3) примут вид:

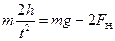. (8)

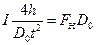. (9)

Решая совместно уравнения (8) и (9), получим рабочую формулу для определения момента инерции маятника Максвелла экспериментальным путем:

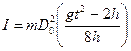. (10)

В формуле (10) масса 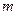является общей массой маятника, включающей в себя массу оси маятника 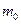, диска ( 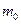+ =126 г) и кольца 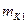- 264 г, - 388 г, 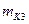- 521 г.