Означення матриці

Лекція №2-3. Елементи теорії матриць

ПЛАН

1. Означення матриці

2. Дії з матрицями

3. Обернена матриця

4. Ранг матриці

Означення матриці

Розглянемо ще один математичний об’єкт, пов’язаний із системою рівнянь (1.1).

Означення 1. Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпців. Якщо повернутися до системи рівнянь (1.1), то коефіцієнти при невідомих у лівій частині якраз і утворюють таку прямокутну таблицю:

.

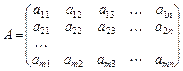Числа 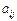називаються елементами матриці, а запис 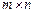означає її розмір. Зауважимо, що на першому місці в цьому запису зазначено кількість рядків матриці, а на другому — кількість стовпців. Наприклад, запис розміру матриці 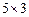означає, що в ній п’ять рядків і три стовпці.

Означення 2. Матриця називається квадратною, якщо кількість рядків матриці дорівнює кількості її стовпців.

Означення 3. Дві матриці рівні між собою, якщо вони мають однаковий розмір і всі їх відповідні елементи рівні між собою.

Елементи з двома однаковими індексами a₁₁, a₂₂, a₃₃, ... a_nn утворюють головну діагональ матриці. Якщо 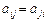, то матриця називається симетричною.

Означення 4. Матриця називається одиничною, якщо дана матриця квадратна і в ній елементи головної діагоналі дорівнюють одиниці, а всі інші нулю.

.

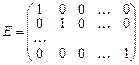Означення 5. Матриця називається трикутною, коли всі елементи матриці, що містяться по один бік від головної діагоналі, дорівнюють нулю, то.

Кожній квадратній матриці можна поставити у відповідність визначник, який складається з тих самих елементів.

.

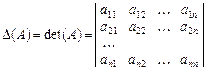Означення 6. Матриця називається неособливою, або не виродженою, якщо її визначник відмінний від нуля.

Означення 7. Матриця називається особливою, або виродженою, якщо її визначник дорівнює нулю.