Дії з матрицями

Означення 8. Сумою матриць одного й того самого порядку 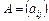і називається матриця 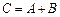; 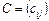, будь-який елемент якої дорівнює сумі відповідних елементів матриць А і В: . Наприклад обидві матриці 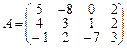, 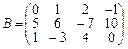мають розмір , тому за означенням можна утворити їх суму — матрицю

.

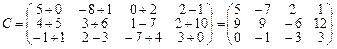Означення 9. Добутком матриці 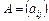на деяке число 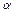називається така матриця С, кожен елемент якої 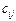утворюється множенням відповідних елементів матриці А на , .

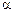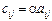Приклад. , .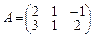

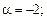
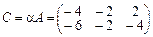Очевидно, що для суми матриць і добутку матриць на число виконуються рівності:

1) ;

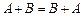2) ;

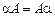3) ;

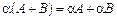4) ,

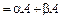5) .

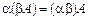Означення 10. Добутком матриці 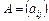розміру 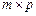на матрицю розміру 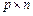називається така матриця 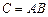розміру 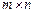, , 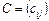кожний елемент можна знайти за формулою:

.

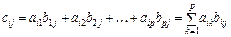Кожний елемент матриці С утворюється як сума добутків відповідних елементів і-го рядка матриці А на відповідні елементи j-го стовпця матриці В, тобто за схемою:

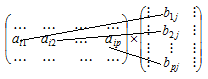
Зазначимо, що в результаті множення дістанемо матрицю розміру .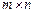

З означення випливає, що добуток матриць некомутативний: .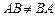

Повернемось до системи рівнянь (1.1) і утворимо матриці: А — коефіцієнтів при невідомих, Х — невідомих, В — вільних членів:

, , .

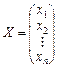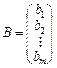Тоді згідно з означенням добутку матриць систему рівнянь (1.1) можна записати в матричному вигляді:

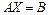, (1.5)

який значно скорочує запис системи рівнянь.

3. Обернена матриця

Означення 11. Матриця А^–1 називається оберненою матрицею до квадратної невиродженої матриці А, якщо виконується співвідношення: .

Нехай дано квадратну матрицю А. Доведемо, що коли , існує обернена матриця А^–1. Розглянемо матрицю:

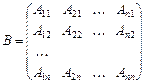. Утворимо добутки і .

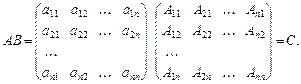
За правилом множення матриць елементи матриці С знаходимо за формулою:

. (1.6)

Якщо i = j, то згідно з формулою (1.3) маємо: 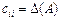, тобто знаходимо значення визначника матриці А; якщо 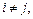то вираз (1.6) є сумою добутків елементів i-го рядка визначника на алгебраїчні доповнення, що відповідають j-му рядку цього самого визначника. За властивістю 9 визначників така алгебраїчна сума дорівнює нулю. Отже, 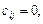якщо i ¹ j. Матриця С набирає вигляду: 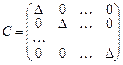. Щоб ця матриця стала одиничною, треба помножити її на .

.

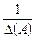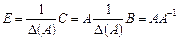Отже, обернена матриця має вигляд:

.

Доведемо, що для матриці А матриця А^–1 єдина. Для цього припустимо протилежне. Нехай існує одна матриця С, така що АС = СА = Е. Тоді

САА^–1 = С(АА^–1) = СЕ = С,

а водночас

САА^–1 = (СА)А^–1 = ЕА^–1 = А^–1, звідси С = А^–1.

Доходимо висновку, що початкове припущення неправильне, тобто обернена матриця єдина.

4. Ранг матриці

Розглянемо матрицю А розміром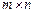

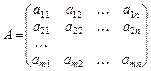
і введемо ще одне важливе поняття.

Означення 12. Рангом матриці А розміром 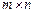називається найвищий порядок відмінного від нуля мінора, утвореного з елементів цієї матриці. Зрозуміло, що 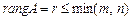, а найбільший можливий ранг матриці може дорівнювати меншому з чисел m і n.

Розглянемо також поняття обвідного мінора k-го порядку. Це буде такий мінор 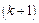-го порядку, який повністю містить у собі мінор k-го порядку.

Обчислюючи ранг матриці, потрібно переходити від мінорів менших порядків, відмінних від нуля, до мінорів більших порядків. Якщо вже знайдено відмінний від нуля мінор М k-го порядку, то достатньо обчислити лише мінори 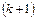-го порядку, що обводять мінор М. Якщо всі вони дорівнюють нулю, то ранг матриці дорівнює k. Якщо серед них знайдеться такий, що відмінний від нуля, то далі для нього будуються обвідні мінори 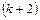-го порядку і т. д.

Означення 13. Елементарними перетвореннями матриці А називаються такі її перетворення:

1) заміна місцями двох рядків або двох стовпців матриці;

2) множення рядка або стовпця матриці на довільне відмінне від нуля число;

3) додавання елементів одного рядка або стовпця до відповідних елементів іншого рядка або стовпця, попередньо помноженого на деяке число.