Закон Кирхгофа

Закон Кирхгофа: отношение спектральной плотности энергетической светимости к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и температуры:

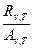= r_v,T (31.6)

Для черного тела А^ч_v,T =1, поэтому из закона Кирхгофа вытекает, что R_v,T для черного тела равна r_v,T. Таким образом, универсальная функция Кирхгофа r_v,T есть не что иное, как спектральная плотность энергетической светимости черного тела. Следовательно, согласно закону Кирхгофа, для всех тел отношение спектральной плотности энергетической светимости к спектральной поглощательной способности равно спектральной плотности энергетической светимости черного тела при той же температуре и частоте.

Из закона Кирхгофа следует, что спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости черного тела (при тех же значеннях Т и v), так как А_v,T < 1, и поэтому R_v,T < r v_υ,T. Кроме того, из (31.6) вытекает, что если тело при данной температуре Т не поглощает электромагнитные волны в интервале частот от v, до v+dv, то оно их в этом интервале частот при температуре Т и не излучает, так как при А_v,T=0, R_v,T=0

Используя закон Кирхгофа, выражение для интегральной энергетической светимости черного тела (31.4) можно записать в виде

R_T= 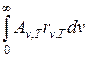. (31.7)

Для серого тела R^с_T = А_T 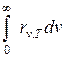= А_TR_е, (31.8)

где R_е = 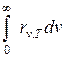-энергетическая светимость черного тела.

Закон Кирхгофа описывает только тепловое излучение, являясь настолько характерным для него, что может служить надежным критерием для определения природы излучения. Излучение, которое закону Кирхгофа не подчиняется, не является тепловым.

Для практических целей из закона Кирхгофа следует, что тела, обладающие темной и шероховатой поверхностью, имеют коэффициент поглощения, близкий к 1. По этой причине зимой предпочитают носить темную одежду, а летом – светлую. Но тела, имеющие коэффициент поглощения, близкий к единице, обладают и соответственно большей энергетической светимостью. Если взять два одинаковых сосуда, один с темной, шероховатой поверхностью, а стенки другого будут светлыми и блестящими, и налить в них одинаковое количество кипящей воды, то быстрее остынет первый сосуд.

31.3. Законы Стефана — Больцмана и смещения Вина

Из закона Кирхгофа следует, что спектральная плотность энергетической светимости черного тела является универсальной функцией, поэтому нахождение ее явной зависимости от частоты и температуры является важной задачей теории теплового излучения.

Стефан, анализируя экспериментальные данные, и Больцман, применяя термодинамический метод, решили эту задачу лишь частично, установив зависимость энергетической светимости R_е от температуры. Согласно закону Стефана — Больцмана,

R_е = σ Т⁴, (31.9)

т. е. энергетическая светимость черного тела пропорциональна четвертей степени его термодинамической температуры; σ — постоянная Стефана — Больцмана: ее экспериментальное значение равно 5,67×10^-8 Вт/(м²×К⁴).

Закон Стефана — Больцмана, определяя зависимость R_е от температуры, не дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных кривых зависимости функции r_λ,T от длины волны λ (r_λ,T = 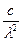´ ´ r_ν,T) при различных температурах (рис.30.2) Рис.31.2.

следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой зависимости r_λ,T от λ и осью абсцисс, пропорциональна энергетической светимости R_е черного тела и, следовательно, по закону Стефана — Больцмана, четвертей степени температуры.

В. Вин, опираясь на законы термо- и электродинамики, установил зависимость длины волны λ_max, соответствующей максимуму функции r_λ,T , от температуры Т. Согласно закону смещения Вина,

λ_max =b/Т, (31.10)

т. е. длина волны λ_max соответствующая максимальному значению спектральной
плотности энергетической светимости r_λ,T черного тела, обратно пропорциональна его термодинамической температуре. b — постоянная Вина ее экспериментальное значение равно 2,9×10^{-3 м}×К.

Выражение (31.10) называют законом смещения Вина, оно показывает смещение положения максимума функции r_λ,T по мере возрастания температуры в область коротких длин волн. Закон Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное при остывании металла).

Формулы Рэлея-Джинса и Планка

Из рассмотрения законов Стефана-Больцмана и Вина следует, что термодинамический подход к решению задачи о нахождении универсальной функции Кирхгофа не дал желаемых результатов.

Строгая попытка теоретического вывода зависимости r_λ,T принадлежит Рэлею и Джинсу, которые применили к тепловому излучению методы статистической физики, воспользовшим классическим законом равномерного распределения энергии по степеням свободы.

Формула Рэлея-Джинса для спектральной плотности энергетической светимости черного тела имеет вид:

r_ν,T = 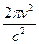<Е> = 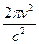kT, (31.11)

где <Е> = kT – средняя энергия осциллятора с собственной частотой ν.

Как показал опыт выражение (31.11) согласуется с экспериментальными данными только в области достаточно малых частот и больших температур. В области больших частот эта формула расходится с экспериментом, а также с законом смещения Вина. И получить закон Стефана–Больцмана из этой формулы приводит к абсурду. Этот результат получил название «ультрафиолетовой катастрофы». Т.е. в рамках классической физики не удалось объяснить законы распределения энергии в спектре черного тела.

В области больших частот хорошее согласие с опытом дает формула Вина (закон излучения Вина):

r_ν,T =Сν³ А е ^–Аν/Т, (31.12)

где r_ν,T - спектральная плотность энергетической светимости черного тела, С и А – постоянные величины. В современных обозначениях с использованием

постоянной Планка закон излучения Вина может быть записан в виде

r_ν,T = 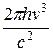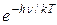. (31.13)

Правильное, согласующееся с опытными данными выражение для спектральной плотности энергетической светимости черного тела было найдено Планком. Согласно выдвинутой квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями – квантами, причем энергия кванта пропорциональна частоте колебаний

Е₀ =hν = hс/λ,

где h=6,625×10^-34Дж×с – постоянная Планка.Так как излучение испускается порциями, то энергия осциллятора Е может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии Е₀

Е = nhν (n = 0,1,2…).

В данном случае среднюю энергию <Е> осциллятора нельзя принимать равной kT.

В приближении, что распределение осцилляторов по возможным дискретным состояниям подчиняется распределению Больцмана, средняя энергия осциллятора равна

<Е> =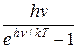 ,(31.14)

а спектральная плотность энергетической светимости определяется по формуле

r_ν,T = 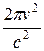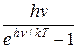.(31.15)

Планк вывел для универсальной функции Кирхгофа формулу

r_ν,T = 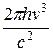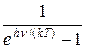, (31.16)

которая согласуется с экспериментальными данными по распределению энергии в спектрах излучения черного тела во всем интервале частот и температур.

Из формулы Планка, зная универсальные постоянные h, k и с, можно вычислить постоянные Стефана-Больцмана σ и Вина b. И наоборот. Формула Планка хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового излучения, т.е. является полным решением задачи теплового излучения.