Кольца Ньютона

Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного слоя, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис.26.1).

Все рассуждения проведены для отраженного света. Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхности воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падении света имеющие вид концентрических окружностей.

Запишем выражение для радиусов колец соответственно: m-^го-светлого кольца:

r_m = 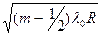, (m=0,1,2,3,…), (26.13)

m-^го- темного кольца:

r_m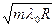^* = , (m=0,1,2,3,…). (26.14)

Измеряя радиусы соответствующих колец, можно (зная радиус кривизны линзы) определить длину волны λ₀ и, наоборот, по известной длине волны λ₀ найти радиус кривизны линзы.

Система светлых и темных и полос получается только при освещении монохроматическим светом. При наблюдении в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску.

Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на λ₀/2, т. е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот.

m- ^ое- темное кольцо:

r_m = 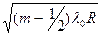, (m=0,1,2,3,…), (26.15)

m-^ое- светлое кольцо:

r_m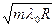^* = , (m=0,1,2,3,…). (26.16)