Работа перемещения контура с током в магнитном поле
Допустим, что провод с током может свободно перемещаться во внешнем магнитном поле. Внешнее полем будем предполагать однородным и перпендикулярным к плоскости контура.
 При указанных на рисунке направлениях тока и поля сила будет направлена вправо и равна
При указанных на рисунке направлениях тока и поля сила будет направлена вправо и равна
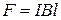 ,
,
где 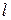 - длина перемещающегося участка тока.
- длина перемещающегося участка тока.
На пути dx эта сила совершит работу
Рис. 16.4.
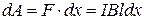 .
.
Произведение 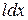 равно заштрихованной площади, а
равно заштрихованной площади, а 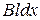 - потоку магнитной индукции
- потоку магнитной индукции 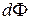 через эту площадь. Поэтому можно написать, что
через эту площадь. Поэтому можно написать, что
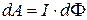 , (16.7)
, (16.7)
где 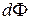 - поток магнитной индукции, пересекаемый проводником при его движении.
- поток магнитной индукции, пересекаемый проводником при его движении.
Полученный результат легко обобщить на случай неоднородного поля. Для этого проводник нужно разбить на участки 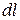 и сложить элементарные работы, совершаемые над каждым участком (в пределах каждой малой площадки
и сложить элементарные работы, совершаемые над каждым участком (в пределах каждой малой площадки 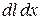 магнитную индукцию можно считать постоянной).
магнитную индукцию можно считать постоянной).
Если вектор 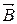 образует с нормалью к контуру угол a, отличный от нуля, направления силы составит с направлением перемещения также угол a и
образует с нормалью к контуру угол a, отличный от нуля, направления силы составит с направлением перемещения также угол a и
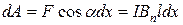 ,
,
где 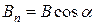 - составляющая вектора
- составляющая вектора 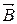 по направлению нормали к площадке
по направлению нормали к площадке 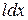 . Произведение
. Произведение 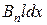 есть
есть 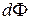 - поток, пересекаемый проводником. Таким образом и в этом случае мы приходим к формуле (16.7).
- поток, пересекаемый проводником. Таким образом и в этом случае мы приходим к формуле (16.7).
 Заметим, что совершается не за счет магнитного поля, а за счет источника, поддерживающего ток в контуре.
Заметим, что совершается не за счет магнитного поля, а за счет источника, поддерживающего ток в контуре.
Найдем работу, совершаемую над замкнутым контуром с током при его перемещении в магнитное поле. Предположим, что контур остается в одной плоскости. Силы, приложенные к участку контура 1-2, образуют с направлением перемещения острые углы. Следовательно, совершаемая ими работа А1 положительна. Эта работа пропорциональна силе тока и пересеченному потоку магнитной индукции
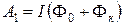 .
.
Силы, действующие на участок 2-1, образуют с направлением перемещения тупые углы. Поэтому совершаемая ими работа А2 отрицательна
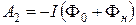 .
.
Работа, совершаемая над всем контуром, равна
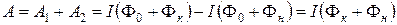
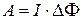 .
.
Дата добавления: 2015-10-05; просмотров: 685;
