Закон Ома. Немецкий физик Г. Ом (1787—1854) экспериментально установил в 1826г., что сила тока I, текущего по однородному металлическому проводнику (т.е

Немецкий физик Г. Ом (1787—1854) экспериментально установил в 1826г., что сила тока I, текущего по однородному металлическому проводнику (т.е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

,

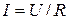где R — электрическое сопротивление проводника. Это уравнение выражает закон Ома для участка цепи(не содержащего источника э.д.с.): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника. Эта формула позволяет установить единицу сопротивления — ом (Ом): 1 Ом—сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А.

Величина 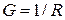называется электрической проводимостью проводника. Единица проводимости — сименс (См): 1 См—проводимость участка электрической цепи сопротивлением 1 Ом. Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S :

,

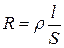где r — коэффициент пропорциональности, характеризующий материал проводника. Он называется удельным электрическим сопротивлением. Единица удельного электрического сопротивления — Ом×метр (Ом×м).

Рассмотрим неоднородный участок цепи, где действующую ЭДС на участке 1-2 обозначим через e₁₂, а приложенную на концах участка разность потенциалов — через j₁- j₂.

Если ток проходит по неподвижным проводникам, образующим участок 1-2,то работа А₁₂ всех сил (сторонних и электростатических), совершаемая над носителями тока, по закону сохранения и превращения энергии равна теплоте, выделяющейся на участке. Работа сил, совершаемая при перемещении заряда q₀ на участке 1-2,

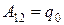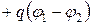e_{12 .} (15.1)

ЭДС e₁₂, как и сила тока I — величина скалярная. Ее необходимо брать либо с положительным, либо с отрицательным знаком в зависимости от знака работы, совершаемой сторонними силами. Если ЭДС способствует движению положительных зарядов в выбранном направлении (в направлении 1—2), то e₁₂>0. Если ЭДС препятствует движению положительных зарядов в данном направлении, то e₁₂<0.

За время t в проводнике выделяется теплота

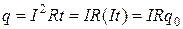. (15.2)

Из формул (15.1) и (15.2) получим 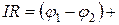e₁₂. (15.3)

Отсюда 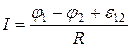. (15.4)

Выражение (15.3) или (15.4) представляет собой закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.

Если на данном участке цепи источник тока отсутствует (e₁₂ =0), то из (15.4) приходим к закону Ома для однородного участка цепи: 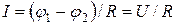(при отсутствии сторонних сил напряжение на концах участка равно разности потенциалов). Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, j₁=j₂; тогда из (15.4) получаем закон Ома для замкнутой цепи: I =e/R, где e — ЭДС, действующая в цепи, R — суммарное сопротивление всей цепи. В общем случае

Рис. 15.2. R=r+R₁, где r—внутреннее сопротивление источника ЭДС, R₁ — сопротивление внешней цепи. По этому закон Ома для замкнутой цепи будет иметь вид I =e /(r+R).