Поляризация диэлектриков. В отсутствии внешнего электрического поля дипольные моменты молекул диэлектрика или равны нулю (неполярные молекулы)

В отсутствии внешнего электрического поля дипольные моменты молекул диэлектрика или равны нулю (неполярные молекулы), или распределены по направлениям в пространстве хаотическим образом (полярные молекулы). В обоих случаях суммарный электрический момент диэлектрика равен нулю. Под действием внешнего поля диэлектрик поляризуется. Результирующий электрический момент единицы объема характеризует степень поляризации диэлектрика. Если поле или диэлектрик неоднородны, степень поляризации в разных точках диэлектрика будет различна. Чтобы охарактеризовать поляризацию в данной точке, нужно выделить заключающий в себе эту точку физически бесконечно малый объем 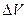, найти сумму 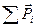моментов, заключенных в этом объеме молекул, и взять отношение

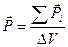, (14.6)

Р – вектор поляризации диэлектрика.

У диэлектриков любого типа (кроме сегнетоэлектриков) вектор поляризации связан с напряженностью поля в той же точке простым соотношением:

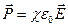, (14.7)

где c - диэлектрическая восприимчивость.

Для диэлектриков, построенных из неполярных молекул, формула (13.7) вытекает из следующих простых соображений. В пределы объема 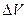попадает количество молекул, равное 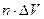, где n – число молекул в единице объема.

.

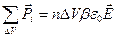Разделив это выражение на 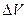, получим вектор поляризации .

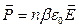Отсюда следует, что .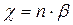

Под напряженностью поля в диэлектрике понимают значение 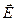, получающееся усреднением истинного поля по физически бесконечно малому объему.

Поле 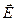получается в результате наложения двух полей: поля 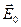, создаваемого свободными зарядами, т.е. такими зарядами, которые могут передаваться от одного тела к другому при их касании, и поля 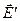связанных зарядов. В силу принципа суперпозиции полей:

. (14.8)

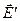Связанные заряды отличаются от свободных лишь тем, что не могут покинуть пределы молекулы (или атома), в состав которой они входят. В остальном их свойства таковы, как и у всех прочих зарядов. В частности, на связанных зарядах начинаются или заканчиваются линий вектора . Поэтому теорему Гаусса для определяемого выражением (1) вектора 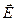нужно записать в виде:

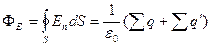. (14.9)

В это выражение входит сумма связанных зарядов не известная нам. Но можно выразить сумму связанных зарядов через поток вектора поляризации:

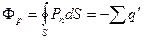. (14.10)

Объединив (14.9) и (14.10) получим:

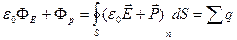. (14.11)

Выражение в скобках называют электрическим смещением или электрической индукцией и обозначают буквой .

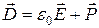. (14.12)

С использованием этой величины формула (14.11) может быть записана в виде:

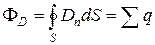. (14.13)

Эта формула выражает теорему Гаусса для вектора электрического смещения: поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных зарядов.

Подставив в формулу (14.12) выражение для 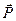, получим:

. (14.14)

Безразмерную величину 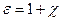(14.15)

называют относительной диэлектрической проницаемостью.

Следовательно, соотношение (14.14) можно записать в виде . Электрическое смещение поля точечного заряда в вакууме равно:

.