Неопределенность и организация системы.

Понятие неопределенности (или энтропии) введено в кибернетику К. Шенноном [6]. Будем делить характе­ристики, описывающие состояние системы в рассматриваемый момент времени, на два класса. Показатели, относящиеся к описа­нию структуры системы, назовем структурным состоянием сис­темы, а остальные показатели- функциональным состоянием системы.

Рассмотрим систему, структура которой может принимать ряд фиксированных дискретных значений S₁, . . ., S_n. Пусть, находясь в любом из своих структурных состояний, система может принимать дискретный набор функциональных состояний F₁,…, F_k . Если долго наблюдать за системой, то по соответ­ствующим частотам появления состояний S_i ( i =1, 2, . . ., n) и F_i (i=1,2, . . ., k) можно оценить вероятности P (S_i) и Р(F_i). Энтропия системы, определяемая ее структурой и состоянием, выражается равенствами:

H_S = - 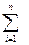P(S_i) _* log₂ P(S_i);(1.3) и H_F = - 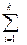P(F_i) _* log₂ P(F_i)(1.4)

Эти величины характеризуют неопределенность системы. Если, любое значение P(S_i) стремится к единице, то неопределенность системы по структуре стремится к нулю. При P(S_i) = 1 система имеет структуру Si и для нее H_S = 0. Систему, неопределенность которой по структуре равна нулю, называют детерминированной по структуре. Аналогичные рассуждения справедливы для P(Fi).

Систему можно характеризовать величиной неопределенности сложного события (I, F), определив соответствующим образом вероятность P(S_i , Fj) = P_i,j нахождения системы в i-том структурном и j-том функциональном состояниях. Для такого события H = - 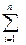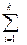P_{i,j *} log₂ P_i,j ; (1.5)

Можно показать, что при P_i,j = 1/nk (i == 1, 2, . . .,n; j =1, 2, . . ., k) неопределенность системы максимальна. Если через H_max обозначить максимально возможную струк­турную и функциональную неопределенность системы, а через Н- фиксированное на данный момент времени значение неопределен­ности и вычислить R= 1- H/ H_max (1.6)

то по ней, можно оценить уровень организации системы. Эту величину называют относительной организацией системы.

Чтобы оценить абсолютную организацию системы, вводят величину I, именуемую абсолютной мерой организации системы. Ее определяют как разность

I= H_max-H

Пример.

1. Ю. Г. Антомонов [5] оценивает относительную организацию рассмотренных выше двух биологических систем следующими величинами: R₁ = 1 - 3,8 _* 10^-6; R₂=1- 6,5 _* 10^-9. Эти величины показывают, что нейронные системы явля­ются практически детерминированными.

2. Оценим относительную и абсолютную организацию простейшей производственной системы. Рассмотрим систему, состоящую из трех элементов, например группу лиц из трех человек. Зануме­руем эти элементы цифрами 1, 2, 3. В такой системе могут существовать связи: 1—2, 2—1; 1—3, 3—1; 2—3 и 3—2. Предположим, что все эти связи равновероятны. Энтропия этой системы будет

Hmax = - 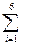Pi * log₂ Pi =- 6/6 _* log₂ 1/6 = 2,58.

Упорядочим рассматриваемую систему, запретив в ней связи 2—3 и 3—2. Если речь идет о группе лиц, то такое упорядо­чение означает, что лицо № 1 назначается старшим группы и что оно, обмениваясь информацией с лицами 2 и 3, принимает оконча­тельные решения. Если считать четыре оставшиеся связи равно­вероятными, то энтропия упорядоченной системы определится следующей величиной: Hmax = - 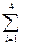Pi * log2 Pi = - 4/4 _* log2 1/4 = 2,00

Отсюда R= 1- H/ H_max = 0,22 и I= H_max - H = 0,58

Контрольные вопросы:

1. Классификация моделей, математическая модель системы.

2. Характеристика моделей имитации и оптимизации.

3. Структура процесса моделирования.

4. Основные этапы моделирования, критерий оптимальности моделирования

5. Система, подсистема, элементы, динамические и статические системы.

6. Связи 1, 2 и 3-го порядков. Обратная связь. Состояние и движение системы.

7. Показатели описа­ния структуры и функционального состояния системы.

8. Неопределенность системы. Как оценить уровень организации системы.