Свойства обратной матрицы.
Если А есть квадратная невырожденная (т.е. её определитель не равен нулю ) матрица, то обратная к ней матрица  обладает следующими свойствами:
обладает следующими свойствами:
1. Обратная матрица перестановочна с А. Оба произведения дают единичную матрицу 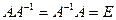 .
.
2. Обратная к А матрица является единственной. 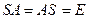 , тогда и только тогда, когда
, тогда и только тогда, когда 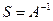 .
.
3. Определитель обратной к А матрицы равен обратной величине определителя матрицы А: 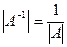 .
.
4. Обратная матрица является невырожденной.
5. Обратной матрицей к  будет матрица
будет матрица 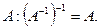
6. Матрица, обратная к транспонированной, равна транспонированной обратной матрице : 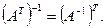
7. Если матрица симметрическая, то такой же будет обратная матрица.
8. Матрица, обратная к произведению матриц, равна произведению обратных матриц, взятых в обратном порядке при условии, что обратные матрицы существуют. Если существуют 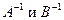 , то
, то 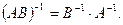
Получение обратной матрицы с помощью ее расчленения на подматрицы.
Вычисление обратной матрицы часто может быть упрощено с помощью расчленения ее на четыре подматрицы, причем верхняя левая и нижняя правая подматрицы должны быть квадратными. 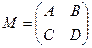 , где A и D – квадратные подматрицы. Процедура получения обратной матрицы
, где A и D – квадратные подматрицы. Процедура получения обратной матрицы 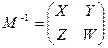 обусловлена тем фактом , что произведение этих матриц должно быть равно единичной матрице
обусловлена тем фактом , что произведение этих матриц должно быть равно единичной матрице 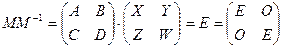 . Отсюда по правилу умножения матриц мы имеем:
. Отсюда по правилу умножения матриц мы имеем:
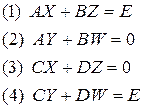
При условии, что A и D- невырожденные матрицы, из (3) следует 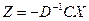 . Подставим в (1) получим
. Подставим в (1) получим 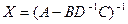 . Аналогично из (2) и (4):
. Аналогично из (2) и (4): 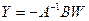 .
.
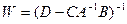 . В соответствии с этими формулами в процессе вычислений потребуется найти четыре обратных матрицы.
. В соответствии с этими формулами в процессе вычислений потребуется найти четыре обратных матрицы.
Если же использовать другое тождество: 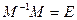 , то мы получим более удобные для расчета выражения
, то мы получим более удобные для расчета выражения 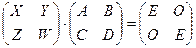 , откуда
, откуда
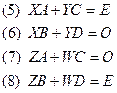
Из (6) следует 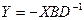 , а из (8)
, а из (8) 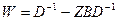 .
. 
Поскольку все восемь уравнений справедливы, то мы можем воспользоваться любыми четырьмя уравнениями, достаточными для нахождения неизвестных матриц.
Первый вариант . Воспользуемся двумя уравнениями из первой четверки – первым и третьим, и двумя уравнениями из второй четверки шестым и восьмым. Соответственно из (1) и (3) получаем выражения для X и Y: 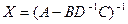 ,
, 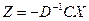 , а из (6) и (8) -
, а из (6) и (8) - 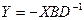 и
и 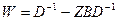 . При проведении расчетов по этим формулам необходимо определить только две обратные матрицы.
. При проведении расчетов по этим формулам необходимо определить только две обратные матрицы.
Порядок расчета следующий:
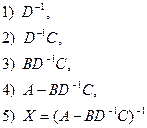

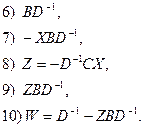
Второй вариант. Можно выбрать другую четверку уравнений (2),(4), (5) и (7). Из них мы получим следующие выражения 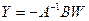 ,
, 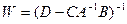 ,
,
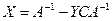 ,
, 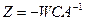 . Приведем полный порядок расчета:
. Приведем полный порядок расчета:
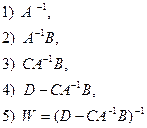
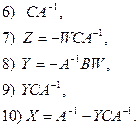
При этом невырожденной в первом случае должна быть матрица D, а во втором A.
Выбор процедуры расчета определяется свойствами матрицы М и ее подматриц. В каждом отдельном случае используются те свойства, которые могут в наибольшей степени упростить расчеты. Например, если 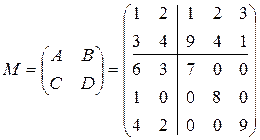 , то лучше пользоваться первым расчетом, т.к. в нем пользуются матрицами
, то лучше пользоваться первым расчетом, т.к. в нем пользуются матрицами 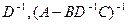 . Эти матрицы довольно легко найти поскольку D – диагональная матрица, а А имеет размеры 2х2.
. Эти матрицы довольно легко найти поскольку D – диагональная матрица, а А имеет размеры 2х2.
Пример 2.С помощью разбиения на клетки обратить матрицу
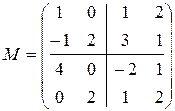
Дата добавления: 2015-10-05; просмотров: 1055;
