Лекция 4. Понятие обратной матрицы. Свойства обратной матрицы. Нахождение обратной матрицы. Вывод общей формулы для обратной матрицы.

Квадратная матрица называется обратной по отношению к данной квадратной матрице, если ее умножение как справа, так и слева на данную матрицу дает единичную матрицу. Для матрицы А обратная матрица обозначается . По определению, .

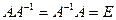Квадратную матрицу называют особенной (или вырожденной), когда ее определитель равен нулю, и неособенной (или невырожденной), когда ее определитель отличен от нуля.

Теорема.Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы определитель матрицы А был отличен от нуля, т.е. чтобы матрица А была неособенной (невырожденной ).

Доказательство. Рассмотрим процесс обращения матрицы. Пусть А – неособенная квадратная матрица n-го порядка, определитель которой не равен нулю. Составим матрицу из алгебраических дополнений элементов данной матрицы и затем транспонируем ее. Полученная матрица называется союзной (или присоединенной) по отношению к матрице А и обозначается :

.

Вычисляя произведения 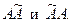по правилам умножения матриц, получим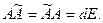

Докажем справедливость этих равенств на примере матрицы третьего порядка. Пусть 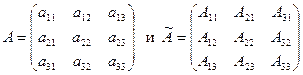, тогда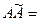

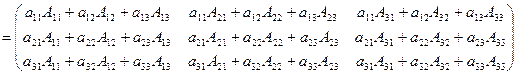
Согласно свойствам определителя все элементы произведения, кроме диагональных, равны нулю. Таким образом, . Так как определитель матрицы А не равен нулю, то .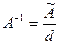

Пример 1. Найти обратную матрицу для матрицы .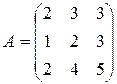

1. Вычисляем определитель данной матрицы

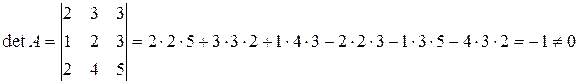Т.к. определитель не равен нулю, то обратная матрица существует.

2. Находим алгебраические дополнения элементов матрицы А.

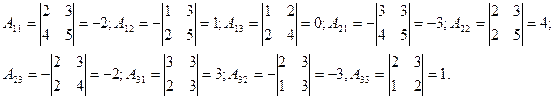
3. Составляем союзную ( присоединенную )матрицу

.

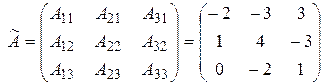4. Вычисляем обратную матрицу .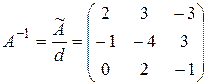

5. Проверка: