Моделирование реакторов идеального смешения (РИС) непрерывного действия
Для упрощения задачи моделирования примем следующие допущения:
1. В реакторе протекает гомогенная химическая реакция;
2. Все компоненты реакционной смеси поступают в реактор в одном потоке;
3. Объем реакционной смеси в аппарате остается неизменным 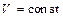 ;
;
4. Теплофизические свойства реакционной смеси не зависят от температуры 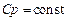 ,
, 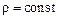 .
.
Эскиз реактора, для которого приемлемы вышеизложенные допущения:
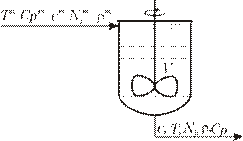
Математическая модель такого реактора строится на основе МИС. Воспользуемся уравнением покомпонентного материального баланса для МИС:
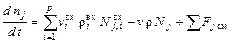 , (1)
, (1)
Исходя из анализа размерностей, выразим количество 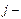 го компонента через его мольную долю в реакционной смеси:
го компонента через его мольную долю в реакционной смеси:
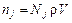 =[ кмоль j/ кмоль] [кмоль /м3] [м3]=[ кмоль j],
=[ кмоль j/ кмоль] [кмоль /м3] [м3]=[ кмоль j],
тогда 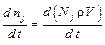 .
.
Рассмотрим третье слагаемое в уравнении (1), характеризующее суммарный молярный поток, образованный источниками и стоками вещества внутри реакционного пространства:
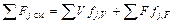
Слагаемое 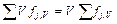 представляет собой сумму объемных источников и стоков вещества, которая, в соответствии с постановкой задачи, определяется только химическими превращениями:
представляет собой сумму объемных источников и стоков вещества, которая, в соответствии с постановкой задачи, определяется только химическими превращениями:
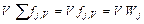 .
.
Слагаемое 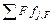 представляет собой сумму поверхностных источников и стоков вещества, которая в данном случае будет равна нулю, так как рассматривается гомогенная реакция и в аппарате не осуществляется никаких процессов протекающих на поверхности контакта фаз, если даже она существует (гетерофазные реакции). Тогда суммарный молярный поток в зоне смешивания будет равен:
представляет собой сумму поверхностных источников и стоков вещества, которая в данном случае будет равна нулю, так как рассматривается гомогенная реакция и в аппарате не осуществляется никаких процессов протекающих на поверхности контакта фаз, если даже она существует (гетерофазные реакции). Тогда суммарный молярный поток в зоне смешивания будет равен:
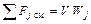
Принимая во внимание, что все исходные вещества подаются в аппарат в одном потоке ( 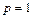 ), преобразуем уравнение (1) к виду:
), преобразуем уравнение (1) к виду:
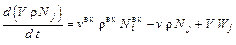 (3)
(3)
Определим концентрацию 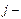 го компонента исходя из анализа размерностей:
го компонента исходя из анализа размерностей:
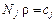 = [кмоль j/кмоль] [кмоль/м3] = [кмольj / м3],
= [кмоль j/кмоль] [кмоль/м3] = [кмольj / м3],
тогда уравнение (3) примет вид:
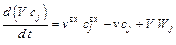 .
.
Поскольку объем реакционной смеси является постоянной величиной, то 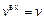 и уравнение (3) может быть преобразовано:
и уравнение (3) может быть преобразовано:
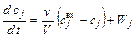
Запишем уравнение теплового баланса для МИС:
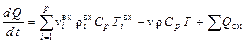 (5)
(5)
Исходя из анализа размерностей, выразим количество теплоты через температуру реакционной смеси:
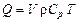 =[м3] [кг/м3] [кДж/(кг К)] [К] =[ Кдж],
=[м3] [кг/м3] [кДж/(кг К)] [К] =[ Кдж],
тогда 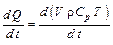 .
.
Рассмотрим третье слагаемое в уравнении (5), характеризующее суммарный тепловой поток, образованный источниками и стоками вещества внутри реакционного пространства:
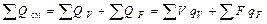
Слагаемое 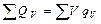 представляет собой сумму объемных источников и стоков теплоты, которая в соответствии с постановкой задачи определяется только процессом химических превращений:
представляет собой сумму объемных источников и стоков теплоты, которая в соответствии с постановкой задачи определяется только процессом химических превращений:
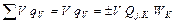 .
.
Слагаемое 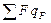 представляет собой сумму поверхностных источников и стоков тепла, которая равна скорости теплообмена с окружающей средой или теплоносителем:
представляет собой сумму поверхностных источников и стоков тепла, которая равна скорости теплообмена с окружающей средой или теплоносителем:
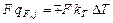
Тогда, учитывая, что в соответствии с постановкой задачи все компоненты реакционной смеси подаются в аппарат в одном входящем потоке, уравнение теплового баланса будет иметь вид:
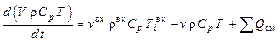 (6)
(6)
Рассмотрим политропический тепловой режим.
Температура реакционной смеси изменяется как за счет химических превращений в объеме реакционной смеси, так и за счет теплообмена с окружающей средой:
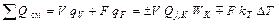 ,
,
где движущая сила процесса теплопередачи равна разности температур реакционной смеси и окружающей среды 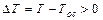 .
.
Преобразуем уравнение (6):
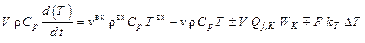
Разделим обе части полученного уравнения на произведение 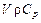 , тогда с учетом того, что
, тогда с учетом того, что 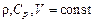 и
и 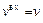 получим:
получим:
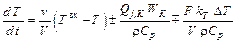 (7)
(7)
Рассмотрим адиабатический тепловой режим.
Температура реакционной смеси изменяется только за счет химических превращений в объеме реакционной смеси:
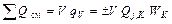 .
.
Тогда уравнение теплового баланса примет вид:
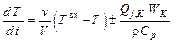 .
.
При изотермическом тепловом режиме процесс протекает без изменения температуры реакционной смеси 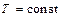 :
:
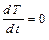
Дата добавления: 2015-10-05; просмотров: 1203;
