Математическое описание объектов химической технологии на основе модели идеального смешения, МИС.

Характеристика МИС: модель идеального смешения характеризуется безградиентностью параметров состояния во всем объеме аппарата.

Параметрами состояния называют все физические и теплофизические характеристики такие, как состав смеси, плотность, теплоемкость, температура и т.д.

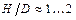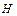Модель идеального смешения предполагает идеальную однородность потоков во всем объеме аппарата в каждый текущий момент времени. Принятие допущения об идеальной однородности справедливо для ёмкостных аппаратов при высокой интенсивности перемешивания. Для ёмкостных аппаратов выполняется соотношение , где – высота аппарата, а 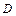его диаметр.

Рисуем аппарат, конструктивные особенности которого позволяют предположить идеальную однородность потоков.

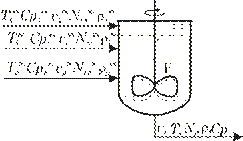
Примем следующие обозначения:

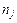– количество 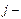го компонента, кмоль j; 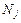– молярная доля 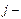го компонента, кмоль j/кмоль; 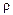– плотность реакционной смеси, молярная – кмоль/м³ и массовая – кг/м³; 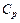– удельная теплоемкость реакционной смеси, кДж/(кг К); 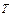– температура реакционной смеси, град. К; 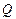– количество теплоты, Кдж; 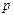– количество входящих потоков.

Запишем покомпонентный материальный баланс, основываясь на общей структуре балансных уравнений.

Рассуждать будем следующим образом. Рассмотрим левую часть структуры балансных уравнений: за промежуток времени, равный 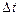количество 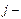го компонента изменится на величину равную 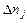. Изменение количества 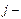го компонента выразится отношением 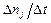. При условии, что промежуток времени выбран таким, что его величина 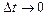и при переходе к пределу, получим: .

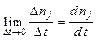Рассмотрим правую часть структуры балансных уравнений. Первое слагаемое характеризует количество 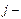го компонента, поступающего в зону проведения процесса посредством всех входящих потоков: 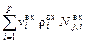. Правильность проверим исходя из анализа размерностей: размерности левой 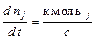и правой 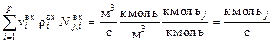частей балансного уравнения совпадают, и, значит, наши рассуждения верны.

Второе слагаемое характеризует количество 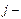го компонента, выходящего из зоны проведения процесса посредством одного выходящего потока – 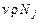. Последнее слагаемое характеризует изменение количества 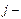го компонента за счет условных источников/стоков, т.е. определяется суммарным молярным потоком 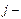го компонента, образованным условными источниками и стоками в зоне смешивания .

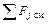Суммарный молярный поток может быть образован как объемными источниками и стоками 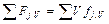, так и поверхностными :

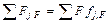Окончательно уравнение покомпонентного материального баланса примет вид:

,

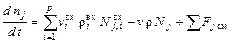где – .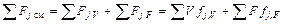

Количество уравнений покомпонентных материальных балансов равно количеству компонентов реакционной смеси .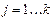

Аналогично рассуждая, запишем уравнение теплового баланса:

,

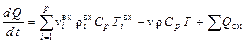где 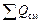– суммарный поток теплоты, образованный условными источниками и стоками в зоне смешивания.

Суммарный поток теплоты определяется как сумма объемных и поверхностных источников и стоков теплоты:

.

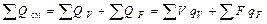Таким образом, математическая модель представляет собой систему дифференциальных уравнений первого порядка. Количество уравнений математической модели равно количеству уравнений материального баланса составленных по каждому компоненту реакционной смеси плюс уравнение теплового баланса.