Энергетика химических реакций.
Энергетическая сторона реакций изучается в разделах химии, называемых термохимией и химической термодинамикой.
Термодинамикана основе энергетических критериев – термодинамических потенциалов дает ответ на вопрос: осуществим ли принципиально тот или иной химический процесс в данных условиях или нет. Изменение термодинамических потенциалов, характеризующее данный процесс, является его движущей силой. Наиболее часто в качестве движущей силы используется изменение энергии Гиббса, или изобарно-изотермического потенциала 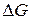 , характеризующего переход процесса из начального в конечное состояние (реагентов, или исходных веществ, в продукты реакции) при постоянстве температуры и давления в системе:
, характеризующего переход процесса из начального в конечное состояние (реагентов, или исходных веществ, в продукты реакции) при постоянстве температуры и давления в системе:
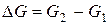 (1)
(1)
Если 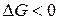 , то процесс принципиально осуществим, если
, то процесс принципиально осуществим, если 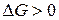 , то процесс невозможен. Чем меньше
, то процесс невозможен. Чем меньше 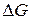 , тем сильнее стремление к протеканию процесса и тем дальше он от состояния равновесия, при котором
, тем сильнее стремление к протеканию процесса и тем дальше он от состояния равновесия, при котором 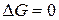 .
.
Изменение энергии Гиббса является результатом вклада двух факторов: энтропийного и энтальпийного.
Энтропийный фактор, характеризующий изменение энтропии системы при переходе из начального в конечное состояние
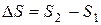 (2)
(2)
отражает стремление системы перейти от более упорядоченного состояния к менее упорядоченному, т.е., от менее вероятного к более вероятному. Значение энтропии тем выше и тем вероятнее характеризуемое ею состояние, чем большим числом микросостояний может быть представлена система. Для неупорядоченной хаотичной системы таких микросостояний огромное множество, поскольку неупорядоченность предполагает огромное количество комбинаций взаимного расположения частиц. Поэтому такая система более вероятна и характеризуется большим положительным значением энтропии. Если же система упорядочена, высокоструктурирована, то находящиеся во взаимном расположении частицы обычно жестко связаны между собой силами химического или межмолекулярного взаимодействия, не имеют достаточно степеней свободы для движения друг относительно друга с образованием новых комбинаций взаимного расположения. Поэтому число микросостояний такой системы невелико, и последняя характеризуется низким значением энтропии. Исходя из изложенного, самопроизвольность процесса определяет положительное значение изменения энтропии: 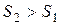 и
и 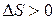 .
.
Энтальпийный фактор, характеризующий тенденцию перехода системы из более высокого энергетического состояния к менее высокому, выражается изменением энтальпии системы при переходе из одного состояния к другому:
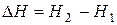 (3)
(3)
Суммарный вклад обоих факторов отражается в выражении изменения изобарно-изотермического потенциала:
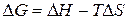 (4)
(4)
Поскольку самопроизвольность процесса определяется неравенством 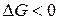 , можно видеть, что этому способствуют положительное изменение энтропии процесса
, можно видеть, что этому способствуют положительное изменение энтропии процесса 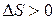 (переход системы из более упорядоченного к менее упорядоченному состоянию) и отрицательное изменение энтальпии процесса
(переход системы из более упорядоченного к менее упорядоченному состоянию) и отрицательное изменение энтальпии процесса 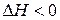 (переход системы из более высокого энергетического состояния к менее высокому).
(переход системы из более высокого энергетического состояния к менее высокому).
В общем случае значение 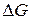 определяется совместным вкладом обоих факторов. В этом плане можно выделить 4 случая.
определяется совместным вкладом обоих факторов. В этом плане можно выделить 4 случая.
1) 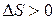 ,
, 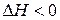 . В этом случае процесс осуществим при любой температуре.
. В этом случае процесс осуществим при любой температуре.
2) 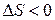 ,
, 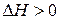 . В этом случае процесс термодинамически запрещен (
. В этом случае процесс термодинамически запрещен ( 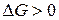 ) во всем диапазоне условий (самопроизвольно будет протекать обратный процесс).
) во всем диапазоне условий (самопроизвольно будет протекать обратный процесс).
3) 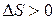 ,
, 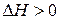 . В этом случае самопроизвольность процесса определяется балансом двух факторов. Самопроизвольному процессу соответствует условие
. В этом случае самопроизвольность процесса определяется балансом двух факторов. Самопроизвольному процессу соответствует условие 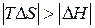 , которому отвечает диапазон температур
, которому отвечает диапазон температур 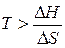 . Можно видеть, что такая ситуация реализуется в области высоких температур, нижний предел которых определяется значением
. Можно видеть, что такая ситуация реализуется в области высоких температур, нижний предел которых определяется значением 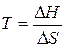 .
.
4) 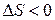 ,
, 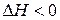 . Как и в предыдущем случае, самопроизвольность процесса определяется балансом энтропийного и энтальпийного факторов. В частности, в соответствии с требованием
. Как и в предыдущем случае, самопроизвольность процесса определяется балансом энтропийного и энтальпийного факторов. В частности, в соответствии с требованием 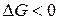 самопроизвольный характер процесса определяется неравенством
самопроизвольный характер процесса определяется неравенством 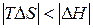 , которому отвечает диапазон температур
, которому отвечает диапазон температур 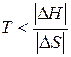 . Такая ситуация реализуется в области низких температур, верхний предел которых определяется значением
. Такая ситуация реализуется в области низких температур, верхний предел которых определяется значением 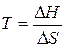 .
.
Из положений (1), (2), (3)) следует, что значения 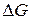 ,
, 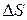 и
и 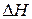 определяются конечным и начальным состоянием системы. Это открывает возможность их определения на основе данных, характеризующих начальное и конечное состояния систем. Для химической реакции
определяются конечным и начальным состоянием системы. Это открывает возможность их определения на основе данных, характеризующих начальное и конечное состояния систем. Для химической реакции
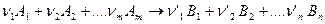 (5)
(5)
изменение энтропии в стандартных условиях (298К, 101,3кПа) определяется равенством:
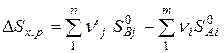 (6)
(6)
где 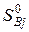 и
и 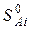 – энтропии j-го и i-го реагента соответственно в стандартных условиях.
– энтропии j-го и i-го реагента соответственно в стандартных условиях.
Значения энтропий различных простых и сложных веществ табулированы в соответствующих справочниках.
Энтальпия процесса (изменение Н) для реакции (5) определяется выражением:
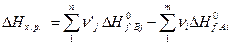 (7)
(7)
где 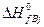 и
и 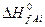 – теплоты образования j-го продукта и i-го реагента из простых веществ в стандартных условиях.
– теплоты образования j-го продукта и i-го реагента из простых веществ в стандартных условиях.
Изменение изобарно-изотермического потенциала для реакции (5) определяется выражением:
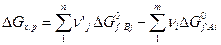 (8)
(8)
где 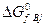 и
и 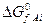 – изменения изобарно-изотермических потенциалов при образовании продуктов реакции и реагентов из простых веществ в стандартных условиях.
– изменения изобарно-изотермических потенциалов при образовании продуктов реакции и реагентов из простых веществ в стандартных условиях.
Очевидно, что движущая сила процесса ( 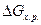 ) может быть рассчитана по формуле (8), если есть прямые данные по
) может быть рассчитана по формуле (8), если есть прямые данные по 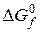 . Если же такие данные отсутствуют, то сначала рассчитываются
. Если же такие данные отсутствуют, то сначала рассчитываются 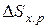 и
и 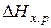 , а затем по уравнению (4) определяют
, а затем по уравнению (4) определяют 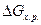 .
.
Значения 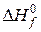 и
и 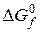 различных сложных веществ приведены в соответствующих справочниках.
различных сложных веществ приведены в соответствующих справочниках. 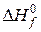 и
и 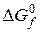 простых веществ равны нулю.
простых веществ равны нулю.
Раздел термодинамики, изучающий тепловые эффекты химических реакций и способы их расчета, называется термохимией.
Теплота химической реакции влияет на энергетическое состояние системы и может иметь важное значение при выборе условий протекания той или иной реакции. Как будет показано ниже, при постоянстве температуры и давления теплота реакции равна энтальпии процесса 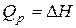 и, таким образом, отражает вклад энергетического фактора в изменение изобарно-изотермического потенциала.
и, таким образом, отражает вклад энергетического фактора в изменение изобарно-изотермического потенциала.
В соответствии с законом сохранения энергии (первый закон термодинамики) теплота, полученная системой, идет на изменение ее внутренней энергии 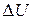 и на совершение работы А:
и на совершение работы А:
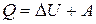 (9)
(9)
Как G и H, внутренняя энергия является функцией состояния системы, и поэтому ее изменение определяется конечным и начальным состоянием:
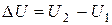 (10)
(10)
Теплота и работа не являются функциями состояния, так как они являются формами передачи энергии и связаны с процессом, а не с состоянием системы.
В химических реакциях А – работа против внешнего давления, т.е. в первом приближении 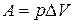 , где
, где 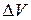 – изменение объема системы
– изменение объема системы 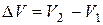 .
.
Так как большинство химических реакций протекает при постоянном давлении, то для изобарно-изотермического процесса ( 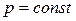 ,
, 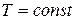 ), теплота реакции будет равна
), теплота реакции будет равна
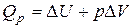
| |
| или | 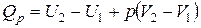
|
| и | 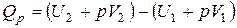 (11) (11)
|
Сумма 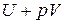 называется энтальпией процесса (Н). Из выражения (11) следует, что теплота процесса в условиях постоянства температуры и давления приобретает свойства функции состояния, т.е. не зависит от пути, по которому протекает процесс, и равна изменению энтальпии системы
называется энтальпией процесса (Н). Из выражения (11) следует, что теплота процесса в условиях постоянства температуры и давления приобретает свойства функции состояния, т.е. не зависит от пути, по которому протекает процесс, и равна изменению энтальпии системы
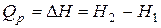
Таким образом, энтальпия является функцией состояния, поскольку ее изменение определяется только начальным и конечным состоянием системы. Нетрудно видеть, что теплота реакции в изохорно-изотермическом процессе (V = const, 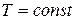 ), при котором
), при котором 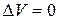 , равна изменению внутренней энергии системы:
, равна изменению внутренней энергии системы:
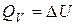 (12)
(12)
Теплоты химических процессов, протекающих при 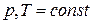 и
и 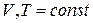 , называются тепловыми эффектами.
, называются тепловыми эффектами.
Расчеты тепловых эффектов основаны на следствии из закона Гесса: тепловой эффект химической реакции равен разности между суммой теплот образования продуктов реакции и суммой теплот образования исходных веществ с учетом стехиометрических коэффициентов перед формулами этих веществ в уравнении реакции.
Количественно расчет тепловых эффектов химических реакций представляется формулой (7). Особенностями расчетов по этому уравнению являются:
– в уравнении (7) значение 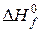 соответствует тому агрегатному состоянию, в котором реагент или продукт реакции входит в стехиометрическое уравнение (5);
соответствует тому агрегатному состоянию, в котором реагент или продукт реакции входит в стехиометрическое уравнение (5);
– коэффициенты уравнения (7) могут быть дробными, если требуется определить тепловой эффект на моль одного из продуктов реакции или реагентов.
В соответствии с законом Гесса тепловой эффект сложного процесса равен сумме тепловых эффектов его стадий. Так, образование оксида углерода (IV) из графита и кислорода можно рассматривать как результат непосредственного взаимодействия простых веществ
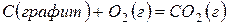 ,
, 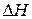 (13)
(13)
или как результат процесса, протекающего через промежуточную стадию образования и сгорания оксида углерода (II)
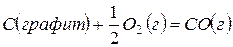 ,
, 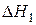 (14)
(14)
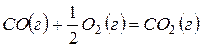 ,
, 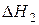 (15)
(15)
Суммируя уравнения (14) и (15), имеем
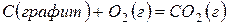 ,
, 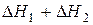 (16)
(16)
Сопоставляя уравнение (13) и (16), имеем 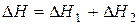 .
.
Дата добавления: 2015-10-05; просмотров: 984;
