Неравноточные измерения
Измерения, выполненные с различной точностью, с неодинаковым числом равноточных наблюдений либо в различных условиях, называют неравноточными.
6.3.1 Понятие о весе независимых измерений. Общая арифметическая середина. Степень надежности результата измерений, выраженную числом, называют весом этого результата. Чем надежнее результат, тем больше его вес. Следовательно, вес связан с точностью результата измерения, которая характеризуется средней квадратической погрешностью. Поэтому вес результата измерения принимают равным величине, обратно пропорциональной квадрату средней квадратической погрешности измерения, т.е.
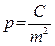
где С – постоянное число;
т – средняя квадратическая погрешность измерения.
Если имеются величины l1, l2, …, ln со средними квадратическими погрешностями т1, т2, …, тп, то их веса будут равны:
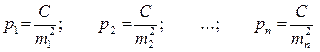
Для облегчения задачи отыскания весов обычно вес одного из результатов с погрешностью m принимают за единицу (т.е. m2 = C) и относительно его вычисляют веса остальных результатов измерений. Тогда веса результатов наблюдений будут равны:
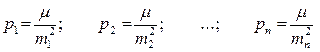
Отсюда
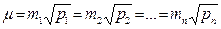 ,
,
т.е. средняя квадратическая погрешность измерения с весом, равным единице, равна произведению средней квадратической погрешности любой измеренной величины на корень квадратный из его веса. Величина m называется средней квадратической погрешностью единицы веса.
Пусть в результате измерений величины получены ее значения l1, l2, …, ln с весами р1, р2, …, рп. Тогда окончательный (наиболее точный) результат из этих измерений может быть найден по формуле весового среднего или общей арифметической середины:
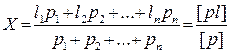
6.3.2 Средние квадратические погрешности единицы веса и общей арифметической середины. Если известны значения истинных погрешностей измерений d1, d2, …, dn, то средняя квадратическая погрешность единицы веса определится по формуле
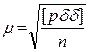
[pdd] = p1d1d1 + p2d2d2 + … + pndndn
где п – число неравноточных измерений;
р1, р2, …, рп – веса измерений.
Определив общую арифметическую середину и найдя уклонения от нее измеренных величин vi = li – X, среднюю квадратическую погрешность единицы веса можно вычислить по общей формуле Бесселя:
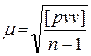
Средняя квадратическая погрешность общей арифметической середины определится из выражения
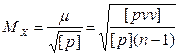
Дата добавления: 2015-10-05; просмотров: 1046;
