Свойства математического ожидания. 1) Математическое ожидание постоянной величины равно самой этой постоянной:
1) Математическое ожидание постоянной величины равно самой этой постоянной:
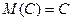 .
.
2) Постоянный множитель можно выносить за знак математического ожидания:
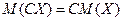 .
.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
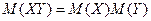 .
.
Это свойство справедливо для произвольного числа случайных величин.
4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
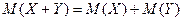 .
.
Это свойство также справедливо для произвольного числа случайных величин.
Пусть производится п независимых испытаний, вероятность появления события А в которых равна р.
Теорема. Математическое ожидание 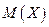 числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
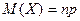 .
.
Дата добавления: 2015-09-29; просмотров: 712;
