Нормирование метрологических характеристик средств измерений. Классы точности средств измерений.

Под нормированиемметрологических зхарактеристик понимают установление номинальных значений и границ допускаемых отклонений реальных метрологических характеристик средст измерений от их номинальных значений.

В соответствии с ГОСТ в ТНПА на средства измерений конкретных типов следует нормировать комплексы метрологических характристик, которые призваны обеспечить решение следующих задач:

1) Определение результатов измерений, проводимых с применение любого экземпляра средства измерений данного типа; 2) расчётное определение характеристик инструментальной составляющей погрешности измерений, проводимых с применением любого экземпляра средства измерений данного тира; 3) расчётное определение метрологических характеристик каналов измерительных систем, в состав которых входит любой экземпляр средства измерений данного типа; 4) оценку метрологической исправности средства измерений данного типа.

При измерениях в производственных условиях, когда не требуется повышенная точность, для оценки возможной максимальной инструментальной составляющей погрешности можно воспользоваться такой характеристикой средства измерений как его класс точности.

Класс точности –обобщённая характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность.

В зависимости от характера изменения погрешностей в пределах диапазона измерении средства измерений различают несколько способов их нормирования:

1) Если аддитивная погрешность средства измерений преобладает над мультипликативной, то чаще всего нормируется предел допускаемой приведенной погрешности. Β_пр.max=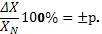

Класс точности в этом случае обозначается положительным числом из стандартизированного ряда: 1*10ⁿ; 1,5*10ⁿ; 2*10ⁿ; 2,5*10ⁿ; 4*10ⁿ; 5*10ⁿ; 6*10ⁿ, где n =1,0,-1,-2 и т.д. Число, обозначающее класс точности, указывается в % предельное значение допускаемой основной приведенной погрешности.

2) Если мультипликативная погрешность преобладает над аддитивной, то нормируется предел допускаемой относительной погрешности.

Класс точности в этом случае обозначается положительным числом из того же радя (6), помещённым в окружность, и указывается в % предельное значение допускаемой основной относительной погрешности.

3) Если имеет место как аддитивная, так и мультипликативная составляющие основной погрешности и они соизмеримы, то нормируется предел допускаемой относительной погрешности.

Класс точности в этом случае обозначается отношением двух положительных чисел c/d из того же рада (4), которое должно удовлетворять условию c/d>1.