Расчет погрешностей. 1. Вычислить погрешность периода колебаний рамки без грузов DTр по методике расчета погрешностей прямых измерений из Приложения
1. Вычислить погрешность периода колебаний рамки без грузов DTр по методике расчета погрешностей прямых измерений из Приложения. Результат измерений записать в виде 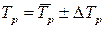 .
.
2. Определить погрешность периода колебаний рамки с грузами DT1 по методике расчета погрешностей прямых измерений из Приложения. Результат измерений представить в виде 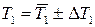 .
.
3. Определить погрешность периода колебаний рамки с образцом DT по методике расчета погрешностей прямых измерений из Приложения. Результат измерений представить в виде 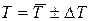 .
.
4. Рассчитать погрешность момента инерции рамки DIp по формуле методики расчета погрешностей косвенных измерений
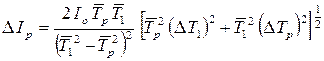 . (5.27)
. (5.27)
Результат эксперимента записать в следующем виде: 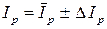 .
.
5. Вычислить погрешность момента инерции твердого тела по формуле метода расчета погрешностей косвенных измерений (a=x, y, z)
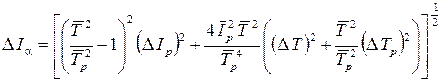 . (5.28)
. (5.28)
Результат эксперимента записать в следующем виде: 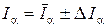 .
.
ГИРОСКОП
Гироскопом называется симметричное твердое тело, быстро вращающееся вокруг оси симметрии, которая может изменять свое направление в пространстве.
Для демонстрационных целей обычно пользуются гироскопами конструкции, которая схематически изображена на рис. 6.1. Колесо гироскопа К (ротор) насажено на ось, которая может поворачиваться как вокруг горизонтальной оси, так и вокруг вертикальной оси, т.е. может принимать любое положение в пространстве. (Отклонения оси по вертикали в этой конструкции ограничены не очень большими углами). Для того, чтобы момент сил тяжести относительно трёх осей гироскопа был равен нулю, центр тяжести гироскопа должен совпадать с точкой пересечения трёх осей вращения. Ротор гироскопа приводится в быстрое вращение при помощи электромотора.
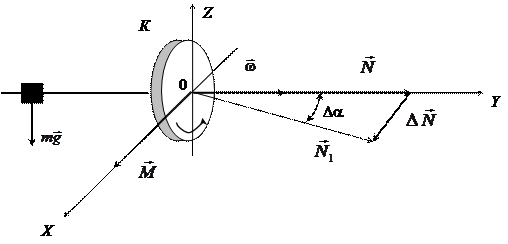 |
Рис. 6.1. Схема опыта
Так как момент силы тяжести относительно точки О равен нулю, то ось вращающегося гироскопа в отсутствие каких-либо других внешних сил остаётся неподвижной. Гироскоп обладает постоянным моментом импульса 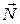 , направленным вдоль неподвижной оси вращения гироскопа. Если на гироскоп начинают действовать внешние силы, то ось гироскопа начинает двигаться – появляется вращение вокруг других осей. Тогда
, направленным вдоль неподвижной оси вращения гироскопа. Если на гироскоп начинают действовать внешние силы, то ось гироскопа начинает двигаться – появляется вращение вокруг других осей. Тогда 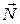 уже не совпадает с осью гироскопа, но всегда остаётся близким к ней. Поэтому, зная, как изменяется вектор
уже не совпадает с осью гироскопа, но всегда остаётся близким к ней. Поэтому, зная, как изменяется вектор 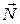 , мы сможем сказать, как приблизительно движется ось гироскопа.
, мы сможем сказать, как приблизительно движется ось гироскопа.
Вращение твёрдого тела определяется уравнением
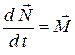 . (6.1)
. (6.1)
Здесь 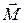 – момент внешних сил,
– момент внешних сил, 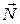 =I
=I 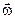 , где I – момент инерции гироскопа, а
, где I – момент инерции гироскопа, а 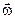 – его угловая скорость. Из уравнения (6.1) видно, что вектор
– его угловая скорость. Из уравнения (6.1) видно, что вектор 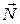 изменяется только тогда, когда действует момент
изменяется только тогда, когда действует момент 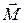 . Следовательно, ось гироскопа может заметно перемещаться только до тех пор, пока действует момент
. Следовательно, ось гироскопа может заметно перемещаться только до тех пор, пока действует момент 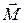 , изменяющий направление
, изменяющий направление 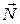 . Изменения же
. Изменения же 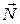 за короткие промежутки времени
за короткие промежутки времени 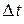 согласно уравнению (6.1) определяются соотношением
согласно уравнению (6.1) определяются соотношением
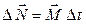 . (6.2)
. (6.2)
При кратковременном действии внешних сил (резкий удар) 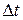 мало, поэтому и D
мало, поэтому и D 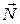 мало –
мало – 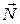 почти не изменяется. Следовательно, очень мало должно изменяться и направление оси гироскопа. Действительно, при резком ударе ось гироскопа не уходит далеко, а дрожит, оставаясь почти на месте.
почти не изменяется. Следовательно, очень мало должно изменяться и направление оси гироскопа. Действительно, при резком ударе ось гироскопа не уходит далеко, а дрожит, оставаясь почти на месте. 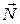 после удара перестаёт изменяться. Но ось гироскопа не должна совпадать с направлением
после удара перестаёт изменяться. Но ось гироскопа не должна совпадать с направлением 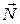 , а должна быть лишь близка к нему. Она может совершать малые движения около направления
, а должна быть лишь близка к нему. Она может совершать малые движения около направления 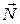 . Такие движения оси гироскопа около направления
. Такие движения оси гироскопа около направления 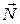 носят название нутаций. Дрожание оси гироскопа после удара и представляет собой один из видов нутаций.
носят название нутаций. Дрожание оси гироскопа после удара и представляет собой один из видов нутаций.
Если гироскоп вращается вокруг своей оси с очень большой
скоростью, то и при наличии небыстрых вращений вокруг других осей вектор момента импульса практически совпадает с осью гироскопа. В дальнейшем мы будем считать, что направление 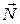 совпадает с осью гироскопа.
совпадает с осью гироскопа.
При длительном воздействии внешних сил вектор 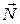 будет изменять своё направление в пространстве. Вместе с ним будет изменять своё направление и ось гироскопа. НаправлениеD
будет изменять своё направление в пространстве. Вместе с ним будет изменять своё направление и ось гироскопа. НаправлениеD 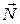 совпадает с направлением
совпадает с направлением 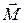 , т.е. не с направлением силы, а с направлением момента силы относительно оси О.Если сбоку надавить на гироскоп с некоторой силой
, т.е. не с направлением силы, а с направлением момента силы относительно оси О.Если сбоку надавить на гироскоп с некоторой силой 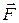 (рис. 6.1), то ось его будет двигаться не в направлении силы, а в направлении момента силы
(рис. 6.1), то ось его будет двигаться не в направлении силы, а в направлении момента силы 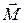 .
.
Если на гироскоп действует сила, создающая постоянный момент 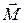 , то направление
, то направление 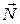 будет изменяться за одинаковые промежутки времени на одинаковую величину D
будет изменяться за одинаковые промежутки времени на одинаковую величину D 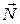 =
= 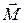 Dt. Если при этом
Dt. Если при этом 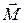 всё время лежит в плоскости движения оси гироскопа, то D
всё время лежит в плоскости движения оси гироскопа, то D 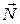 лежит в той же плоскости; вектор
лежит в той же плоскости; вектор 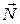 будет оставаться в этой же плоскости и вращаться с постоянной скоростью. Вместе с ним будет вращаться и ось гироскопа. Такое движение оси носит название прецессии.
будет оставаться в этой же плоскости и вращаться с постоянной скоростью. Вместе с ним будет вращаться и ось гироскопа. Такое движение оси носит название прецессии.
Прецессию гироскопа можно продемонстрировать, повесив на ось гироскопа небольшой груз массой m (рис. 6.1) на расстоянии r. Сила тяжести 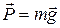 будет создавать момент
будет создавать момент 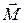 , всё время лежащий в горизонтальной плоскости. В присутствии груза ось гироскопа вращается в горизонтальной плоскости с постоянной скоростью.
, всё время лежащий в горизонтальной плоскости. В присутствии груза ось гироскопа вращается в горизонтальной плоскости с постоянной скоростью.
Вычислим угловую скорость вращения оси гироскопа.
За время Δt ось гироскопа поворачивается на угол
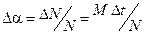 .
.
Учитывая соотношение (6.2), для угловой скорости вращения оси (скорости прецессии) получим
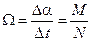 . (6.3)
. (6.3)
Так как 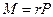 , а
, а 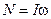 , соотношение (6.3) перепишем в виде
, соотношение (6.3) перепишем в виде
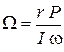 . (6.4)
. (6.4)
Из полученного выражения следует, что чем меньше момент внешних сил, действующих на гироскоп, и чем больше момент импульса гироскопа, тем меньше скорость его прецессии.
Если подталкивать прецессирующий гироскоп в направлении прецессии, то конец оси, на котором висит груз, будет подниматься. Наоборот, если давить на гироскоп против направления прецессии, то конец оси с грузом будет опускаться. Внешние силы, препятствующие прецессии, приводят к тому, что груз опускается. При прецессии на вертикальную ось действуют силы трения в подшипнике, препятствующие прецессии, поэтому ось прецессирующего гироскопа не остаётся в горизонтальной плоскости – конец оси, на котором висит груз, постепенно опускается.
Прецессия гироскопа происходит с постоянной скоростью, пока действует внешний момент, и прекращается сразу же, как только исчезает внешний момент. Движение оси гироскопа не обладает инерцией. Это связано с тем, чтоскоростьвращения оси определяется действующими силами. Инерция же есть проявление того, что ускорения определяются силами.
Во всех описанных опытах не только внешние силы действуют на гироскоп, но и гироскоп действует на те тела, которые являются источником этих сил. Когда мы надавливаем рукой на ось гироскопа, то гироскоп с такой же силой давит на руку. Если гироскоп жёстко связан с некоторым телом, то при всяком движении этого тела, сопровождающемся изменением направления оси гироскопа, возникают силы, действующие на тело со стороны гироскопа. Эти силы часто играют заметную роль.
Например, вращающиеся части машин корабля представляют собой гироскоп, обладающий большим моментом импульса. При килевой качке корабля (когда нос корабля поднимается и опускается) изменяется направление момента импульса машины. Вследствие этого возникают силы давления со стороны вала на подшипники. Эти силы лежат в горизонтальной плоскости и поворачивают корабль вокруг вертикальной оси. Это «ориентирование по курсу» заметно у малых судов с мощными машинами (буксиры).
Силы, возникающие при изменении направления оси вращения гироскопа, могут быть использованы для придания устойчивости судну (уменьшения качки). Для этой цели применяются огромные гироскопы с большой скоростью.
Все описанные свойства гироскопа объясняются тем, что движение оси гироскопа подчиняется уравнению (6.1). Движение оси гироскопа определяется не направлением силы, а направлением момента внешних сил. Но этот момент определяется силами, действующими извне на весь прибор в целом, только тогда, когда гироскоп вполне свободен, т.е. когда конструкция прибора допускает любое положение оси гироскопа. Если же гироскоп не вполне свободен, то нужно принимать во внимание и моменты тех сил, которые могут действовать на ось гироскопа со стороны подшипников, в которых он закреплён.
Эти моменты сил могут совершенно изменить поведение гироскопа под действием внешних сил. Например, если закрепить вертикальную ось и сделать возможным вращение оси гироскопа только в горизонтальной плоскости, то он становится совершенно «послушным». Под действием силы 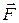 , приложенной к гироскопу в горизонтальной плоскости, ось гироскопа начинает вращаться в направлении действия силы. Это изменение в поведении гироскопа объясняется тем, что наряду с моментом силы
, приложенной к гироскопу в горизонтальной плоскости, ось гироскопа начинает вращаться в направлении действия силы. Это изменение в поведении гироскопа объясняется тем, что наряду с моментом силы 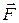 на ось действует момент сил и со стороны подставки, в которой он закреплён. Возникновение этого момента легко объяснить. Вначале, пока на гироскоп не действует сила
на ось действует момент сил и со стороны подставки, в которой он закреплён. Возникновение этого момента легко объяснить. Вначале, пока на гироскоп не действует сила 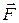 , на него не действуют моменты и со стороны подставки. Гироскоп « не знает», что он закреплён. Поэтому сначала он ведёт себя как вполне свободный гироскоп: под действием силы
, на него не действуют моменты и со стороны подставки. Гироскоп « не знает», что он закреплён. Поэтому сначала он ведёт себя как вполне свободный гироскоп: под действием силы 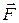 , создающей момент, направленный вертикально вверх, конец оси гироскопа начинает подниматься.
, создающей момент, направленный вертикально вверх, конец оси гироскопа начинает подниматься.
Вертикальная ось, с которой жёстко связана ось гироскопа, немного изгибается, и возникает момент упругих сил, действующих на ось гироскопа. Под действием этого момента 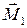 ось гироскопа будет перемещаться в горизонтальной плоскости как раз в том направлении, в котором действует сила
ось гироскопа будет перемещаться в горизонтальной плоскости как раз в том направлении, в котором действует сила 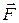 . Поэтому несвободный гироскоп является «послушным»: его ось поворачивается туда, куда её стремится повернутьвнешняя сила. У свободного же гироскопа ось поворачивается в плоскости, перпендикулярной силе.
. Поэтому несвободный гироскоп является «послушным»: его ось поворачивается туда, куда её стремится повернутьвнешняя сила. У свободного же гироскопа ось поворачивается в плоскости, перпендикулярной силе.
Если к вращающемуся гироскопу приложить пару сил, стремящихся повернуть его около оси, перпендикулярной к оси вращения, то гироскоп действительно будет поворачиваться, но только вокруг третьей оси, перпендикулярной к первым двум.
Более детальный анализ явлений, аналогичных описанным выше, показывает, что гироскоп стремится расположить ось своего вращения таким образом, чтобы она образовала возможно меньший угол с осью вынуждаемого вращения и чтобы оба вращения совершались в одном и том же направлении.
Это свойство гироскопа используется в гироскопическом компасе, получившем широкое распространение, в особенности в военном флоте. Гирокомпас представляет собой быстро вращающийся волчок (мотор трёхфазного тока, делающий 25 000 об./мин), который на особом поплавке плавает в сосуде со ртутью и ось которого устанавливается в плоскости меридиана. В данном случае источником внешнего вращающего момента является суточное вращение Земли вокруг её оси. Под его действием ось вращения гироскопа стремится совпасть по направлению с осью вращения Земли, а так как вращение Земли действует на гироскоп непрерывно, то ось гироскопа принимает это положение, т.е. устанавливается вдоль меридиана и продолжает в нем оставаться совершенно так же, как обычная магнитная стрелка. Гироскопические компасы обладают по сравнению с магнитным рядом преимуществ. На их показания не влияют находящиеся поблизости массы железа, они не чувствительны к магнитным бурям и т.д.
Гироскопы часто применяют в качестве стабилизаторов. Их устанавливают для уменьшения качки на океанских пароходах. Были сконструированы также стабилизаторы для однорельсовых железных дорог; массивный быстро вращающийся гироскоп, помещаемый внутри вагона однорельсовой дороги, препятствует опрокидыванию вагона. Роторы для гироскопических стабилизаторов изготовляют от 1 до 100 и более тонн.
Дата добавления: 2015-09-29; просмотров: 1411;
