Обработка результатов эксперимента. 1. Определить период колебаний Тр рамки без грузов в п.2 по формуле (5.17) для каждого измерения

1. Определить период колебаний Т_р рамки без грузов в п.2 по формуле (5.17) для каждого измерения. Найти среднее значение периода .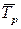

2. Определить период колебаний Т₁ рамки с грузами в п.3 по формуле (5.17) для каждого измерения. Найти среднее значение периода 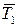. Вычислить момент инерции двух эталонных цилиндрических грузов на основании теоремы Штейнера по формуле

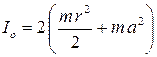, (5.23)

где m – масса груза; r – радиус основания цилиндрического груза; 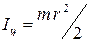– момент инерции одного груза относительно его геометрической оси; a – расстояние от оси вращения рамки до оси грузов.

3. Определить момент инерции рамки, используя результаты п.1 и 2, по формуле

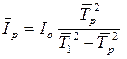. (5.24)

4. Вычислить для куба моменты инерции по измеренным значениям периодов в п.5 и формулам (5.15), (5.18). Сравнить их с теоретическим значением, определенным по формуле 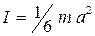, где m – масса куба; a – сторона куба.

5. Вычислить для однородного симметричного параллелепипеда по измерениям п.6 моменты инерции относительно главных осей I_x, I_y, I_z по формулам (5.15) и относительно осей, перпендикулярных его большому ребру, то есть лежащих в плоскости XOY, по формуле (5.19). Сравнить с теоретическими значениями, вычисленными по формулам

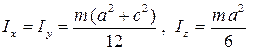, (5.25)

где m – масса параллелепипеда; a=b, c – стороны симметричного параллелепипеда.

6. Вычислить моменты инерции несимметричного прямоугольного параллелепипеда относительно его главных осей инерции по формулам (5.15) и сравнить с теоретическими значениями

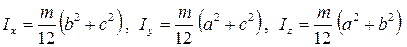. (5.26)

7. Проверить, что для измеренных значений периодов несимметричного параллелепипеда выполняются соотношения (5.21) и (5.22).