Определение скорости полета «пули» баллистическим методом с помощью унифилярного подвеса

Баллистика – наука о движении ракет, снарядов, мин и других тел при стрельбе. Баллистическая траектория снаряда – траектория движения снаряда под действием силы тяжести и силы лобового сопротивления воздуха.

В данной лабораторной работе исследуют движение «пули» в виде кольца, выпущенного из пружинного пистолета. Мишень, в которую производятся выстрелы, представляет собой диск, покрытый слоем пластилина. Мишень присоединяется к унифилярному подвесу – рамке, закрепленной на натянутой стальной нити. После попадания пули в мишень рамка начинает вращаться вокруг вертикальной оси. Если пренебречь моментом сил трения при движении рамки, то рамку и «пулю» можно рассматривать как замкнутую систему тел и использовать для них закон сохранения момента импульса.

Момент импульса «пули» перед соударением 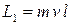, где m – масса «пули», v – его скорость, l – прицельное расстояние (рис. 4.1). После соударения рамка с грузами приходит во вращение с угловой скоростью w, при этом ее момент импульса

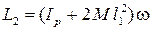. (4.1)

Здесь I_p – момент инерции рамки без грузов; M – масса каждого из грузов; l₁ – расстояние грузов от оси вращения. Вкладом в момент инерции прилипшей «пули» можно пренебречь из-за малости его массы. Момент инерции тела относительно некоторой оси равен сумме моментов инерции частей тела относительно той же оси.

По закону сохранения момента импульса L₁=L₂ получаем

v 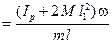. (4.2)

Чтобы воспользоваться этой формулой, нужно найти угловую скорость рамки w в момент соударения и момент инерции рамки с грузами .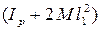

Угловую скорость можно найти по углу максимального отклонения j_m рамки после соударения. После соударения вращение рамки тормозится под действием момента упругих сил в нити подвеса. При этом выполняется закон сохранения энергии вращения. Кинетическая энергия рамки переходит в потенциальную энергию закрученной нити

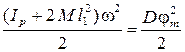, (4.3)

где D – модуль кручения проволоки. Модулем кручения называется коэффициент пропорциональности между моментом упругих сил M_упр и углом закручивания нити j:

.

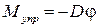Знак минус здесь показывает, что направление момента упругих сил противоположно углу закручивания.

Из соотношения (4.3) находим выражение для угловой скорости:

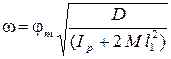. (4.4)

Модуль кручения D и момент инерции ( 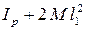) определяют значение периода колебаний рамки. Их отношение, а также необходимый для вычисления скорости момент инерции рамки с грузами можно найти из измерений периода колебаний рамки с грузами и без них. Для того, чтобы понять, как связан период с этими величинами, рассмотрим уравнение вращения рамки, подвешенной на упругой нити. На основании закона динамики вращательного движения M=I e записывается уравнение

.

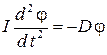Здесь I – момент инерции рамки в общем случае; 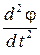– вторая производная от угла по времени, т.е. угловое ускорение e. Это уравнение приводится к виду

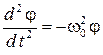, (4.5)

где 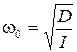. Уравнение (4.5) описывает гармонические колебания с циклической частотой колебаний w₀. Период колебаний вычисляется по формуле

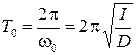. (4.6)

Обозначим период колебаний рамки без грузов T₁, с грузами T, по формуле (4.6) имеем

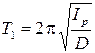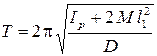, . (4.7)

Из этих формул получим для угловой скорости (4.4) следующее выражение:

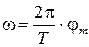. (4.8)

Исключая модуль кручения из формулы (4.7), находим момент инерции рамки с грузами:

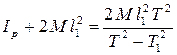. (4.9)

Подстановка соотношений (4.8) и (4.9) в уравнение (4.2) дает окончательную формулу для определения скорости

v 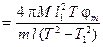. (4.10)