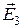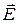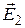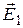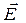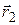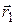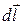НАПРЯЖЁННОСТЬ ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА
Найдём напряжённость Е электростатического поля, создаваемого точечным зарядом q, находящимся в однородном изотропном диэлектрике, в точке, отстоящей от него, на расстоянии r. Мысленно поместим в эту точку пробный заряд q0. Тогда 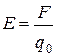 и
и  ×Отсюда получаем, что
×Отсюда получаем, что
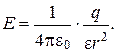 (4)
(4)
СУПЕРПОЗИЦИЯ ПОЛЕЙ
Пусть имеется система точечных электрических зарядов q1, q2,..., qn. Тогда напряжённость электрического поля, создаваемой этими зарядами, в произвольной точке вычисляется по формуле:
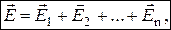 (5)
(5)
т.е. напряжённость поля системы зарядов равна векторной сумме напряжённостей полей, которые создаёт каждый заряд системы в отдельности. Соотношение (5) называютпринципом суперпозиции полей.
ЛИНИИ НАПРЯЖЁННОСТИ
Для наглядного изображения электрического поля пользуются линиями напряжённости или силовыми линиями. Линией напряжённости называют такую линию, в каждой точке которой вектор напряжённости электрического поля направлен по касательной к ней. Направление этих линий совпадает с направлением поля. Условились эти линии проводить так, чтобы число линий, отнесённых к единице площади площадки, расположенной перпендикулярно к ним, равнялось
  
   Рис. 1 Рис. 1
|
бы модулю напряжённости поля в месте расположения площадки. При таком способе построения по густоте линий напряжённости можно судить о модуле напряжённости электрического поля в различных точках поля. Там, где линии расположены гуще, модуль напряжённости поля больше. Следует отметить, что линии напряжённости никогда не пересекаются, поскольку их пересечение означало бы отсутствие определённого направления вектора 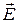 в точках их пересечения. Картина линий напряжённости для неоднородного электростатического поля приведена на рис. 1. Из этого рисунка видно E3 < E2 < E1. Об этом судят по густоте линий. Условились считать, что линии напряжённости начинаются на положительных зарядах и оканчиваются на отрицательных.
в точках их пересечения. Картина линий напряжённости для неоднородного электростатического поля приведена на рис. 1. Из этого рисунка видно E3 < E2 < E1. Об этом судят по густоте линий. Условились считать, что линии напряжённости начинаются на положительных зарядах и оканчиваются на отрицательных.
ПОТОК НАПРЯЖЁННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
1. Потоком напряжённости электрического поля через какую-либо поверхность называют число линий напряженности 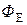 , пронизывающих её. Пусть площадка S находится в однородном электростатическом поле. При этом она перпендикулярна к линиям напряженности. Поскольку через единицу площади проходит число линий напряжённости, равное Е, то элементарный поток через эту площадку равен ФE = ES.
, пронизывающих её. Пусть площадка S находится в однородном электростатическом поле. При этом она перпендикулярна к линиям напряженности. Поскольку через единицу площади проходит число линий напряжённости, равное Е, то элементарный поток через эту площадку равен ФE = ES.
Рассмотрим теперь случай, когда в однородном электростатическом поле находится плоская площадка, нормаль 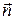 к площадке составляет угол a с направлением поля, т.е. с вектором напряжённости
к площадке составляет угол a с направлением поля, т.е. с вектором напряжённости 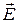 (рис. 2). Число линий напряжённости, проходящих через площадку S и её проекцию Sпрна плоскость, перпендикулярную к этим линиям, одинаково. Следовательно, поток
(рис. 2). Число линий напряжённости, проходящих через площадку S и её проекцию Sпрна плоскость, перпендикулярную к этим линиям, одинаково. Следовательно, поток 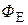 напряжённости электрического поля через них одинаков. Используя выражение предыдущую формулу, находим, что
напряжённости электрического поля через них одинаков. Используя выражение предыдущую формулу, находим, что 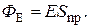 Но Sпр= S cosa. Поэтому
Но Sпр= S cosa. Поэтому
ФЕ = ES cos a = EnS, (6)
где E×cos a = En¾ проекция вектора 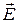 на направление нормали
на направление нормали 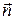 к площадке.
к площадке.
   
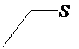

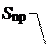                      Рис. 2 Рис. 3 Рис. 2 Рис. 3
|
Для вычисления потока ФЕ напряжённости электрического поля через произвольную поверхность S, помещённую в неоднородное электрическое поле (рис. 3), надо мысленно разбить его на элементарные участки dS, чтобы площадку можно было бы считать плоской, а поле в её пределах однородным. Тогда, согласно (6), элементарный поток dФE = En dS, а поток напряжённости электрического поля через всю поверхность равен сумме этих потоков dФE, т.е.
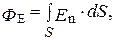 (7)
(7)
поскольку суммирование бесконечно малых величин означает интегрирование.
ТЕОРЕМА ГАУССА ДЛЯ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Проведём вокруг точечного заряда сферу произвольного радиуса r с центром в точке расположения заряда (рис. 3). Найдём поток напряжённости электростатического поля через эту поверхность. В данном случае направления векторов 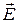 и
и 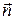 в любой точке поверхности совпадают. Поэтому En = E×cos 0° = E. Модуль напряжённости во всех точках на поверхности сферы одинаков и равен
в любой точке поверхности совпадают. Поэтому En = E×cos 0° = E. Модуль напряжённости во всех точках на поверхности сферы одинаков и равен 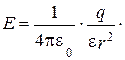 C учётом этого из (6) получаем:
C учётом этого из (6) получаем:
|


    Рис. 3 Рис. 3
|
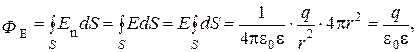 (8)
(8)
где значок °на интеграле означает, что интегрирование производится по замкнутой поверхности. E вынесена за знак интеграла, поскольку она не зависит от S. Суммирование же всех площадей элементарных площадок даёт площадь S сферы, т.е. 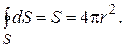 Соотношение (8) справедливо не только для сферы, но и для любой замкнутой поверхности, поскольку число линий напряжённости, пронизывающих её и сферу, одинаково. Если имеется система точечных зарядов, то очевидно, что полный поток ФЕ напряжённости электрического поля через замкнутую поверхность в силу принципа суперпозиции полей равен сумме потоков ФЕi, создаваемых каждым зарядом qiв отдельности, т.е.
Соотношение (8) справедливо не только для сферы, но и для любой замкнутой поверхности, поскольку число линий напряжённости, пронизывающих её и сферу, одинаково. Если имеется система точечных зарядов, то очевидно, что полный поток ФЕ напряжённости электрического поля через замкнутую поверхность в силу принципа суперпозиции полей равен сумме потоков ФЕi, создаваемых каждым зарядом qiв отдельности, т.е. 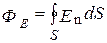 =
= 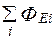 . Но, как следует из (8), ФEi = qi/ (e0e). Поэтому
. Но, как следует из (8), ФEi = qi/ (e0e). Поэтому
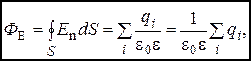 (9)
(9)
поскольку e0и e постоянные величины их вынесли за знак суммы. Таким образом, получен общий результат, названный теоремой Гаусса: поток напряжённости электростатического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, заключённых внутри неё, делённой на электрическую постоянную и диэлектрическую проницаемость среды.
Заряды в пространстве могут распределяться не только дискретно, но и непрерывно. В этом случае вводится понятие о плотности зарядов. При непрерывном распределении зарядов по объёму вводят объёмную плотность заряда. Пусть заряд q равномерно распределён по объёму V. Тогда объёмной плотностью заряда r называется отношение r = q/V. Если же распределение заряда неравномерное, то надо выделить на поверхности элементарный участок dV, в пределах которого заряд dq, находящийся на нём, можно считать равномерно распределённым. Объёмная плотность заряда r находится по формуле:
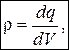 (10)
(10)
т.е. объёмная плотность зарядов равна заряду, приходящемуся на единицу объёма. Используя (6.8), по аналогии с (6.7) можно найти заряд, расположенный в некотором объёме V:
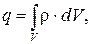 (11)
(11)
Здесь интегрирование производится по всему объёму V, по которому распределён заряд. Тогда при непрерывном распределении заряда на некоторому объёму
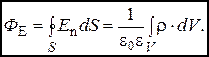 (12)
(12)
§8. РАБОТА СИЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ПРИ ПЕРЕМЕЩЕНИИ ЗАРЯДА.
При движении зарядов в электрическом поле силы, действующие на него со стороны поля, совершают работу. Пусть в начальный момент времени заряд находится в точке 1, определяемой радиус-вектором  а затем по произвольной траектории он перемещается в точку 2 с радиус-вектором
а затем по произвольной траектории он перемещается в точку 2 с радиус-вектором 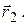 Работу A12, совершаемую силой
Работу A12, совершаемую силой 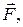 находим по формуле:
находим по формуле: 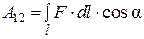 . Из рис. 4 видно, что dl×cosa = dr, где dr ¾ проекция dl на направление радиус-вектора
. Из рис. 4 видно, что dl×cosa = dr, где dr ¾ проекция dl на направление радиус-вектора 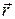 , т.е. элементарное приращение модуля радиус-вектора. С учётом этого
, т.е. элементарное приращение модуля радиус-вектора. С учётом этого 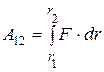 . В данном случае на заряд q0действует кулоновская сила
. В данном случае на заряд q0действует кулоновская сила 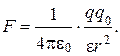 Подставляя это выражение в предыдущую формулу, получаем:
Подставляя это выражение в предыдущую формулу, получаем:
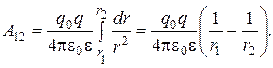 (13)
(13)
|


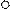 
  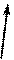     Рис. 4 Рис. 4
|
Из полученного соотношения видно, что работа сил электростатического поля, создаваемого точечным зарядом, определяется только начальным и конечным положением заряда, и, следовательно, не зависит от формы траектории движения. Оказывается, что этим свойством обладает любое электростатическое поле, а не только поле точечного заряда. Следовательно, электростатическое поле является потенциальным.
ЦИРКУЛЯЦИЯ НАПРЯЖЁННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Из выражения (13) следует также, что при переносе заряда по замкнутому пути, т.е., когда заряд возвращается в исходное положение, r1= r2и A12= 0. Тогда запишем 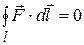 . Значок °на интеграле означает, что интегрирование производится по замкнутой кривой. Но сила
. Значок °на интеграле означает, что интегрирование производится по замкнутой кривой. Но сила 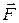 , действующая на заряд q0, равна
, действующая на заряд q0, равна 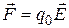 . Поэтому последнюю формулу перепишем в виде:
. Поэтому последнюю формулу перепишем в виде: 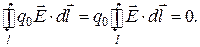 Разделив обе части этого равенства на q0, находим:
Разделив обе части этого равенства на q0, находим:
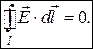 (14)
(14)
Выражение вида 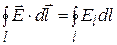 называетсяциркуляцией напряжённости электрического поля. Как указывалось, электростатическое поле потенциально. Для него циркуляция напряжённости равна нулю. Поэтому формулу (14) рассматривают как условие потенциальности поля.
называетсяциркуляцией напряжённости электрического поля. Как указывалось, электростатическое поле потенциально. Для него циркуляция напряжённости равна нулю. Поэтому формулу (14) рассматривают как условие потенциальности поля.
Дата добавления: 2015-09-29; просмотров: 3068;