Минимизация функций с использованием карт Карно
При использовании этого метода логическая функция записывается в виде карты Карно, как было показано в п. 1.4. Напомним, что столбцы и строки карты Карно обозначаются в коде Грея. Тогда клетки, которые могут склеиваться, находятся рядом друг с другом.
Минимальную ДНФ получают, охватывая клетки, содержащие логическую 1, областями прямоугольной формы. Области должны содержать 2kклеток, где к— целое число (2К=1,2; 4; 8; ...). Для каждой области составляется комбинация, в которой различающиеся разряды отмечаются символом (*).
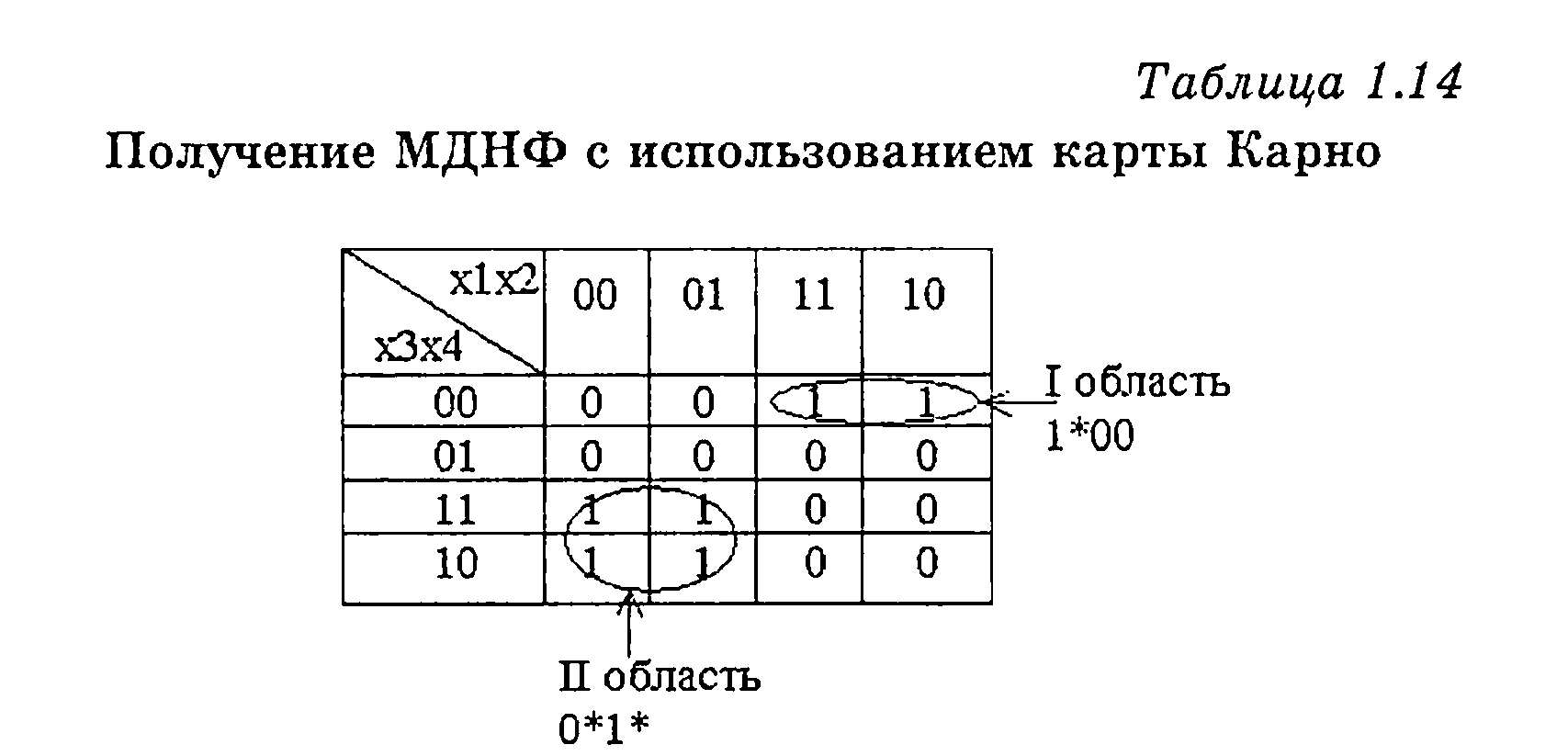
При минимизации логической функции, представленной картой Карно (таблица 1.14) получаем две области. Первой области соответствует набор 1*00, второй области — набор 0*1*. Следовательно, минимальная ДНФ (МДНФ) записывается в виде
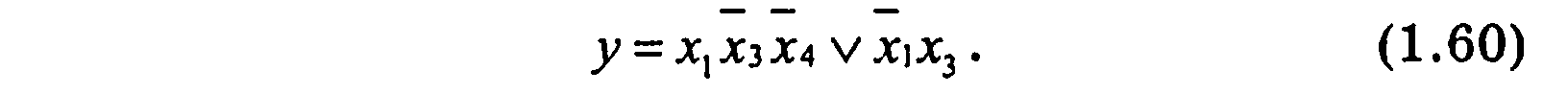 Чтобы получить минимальную КНФ в карте Карно аналогичными прямоугольными областями охватываются нулевые клетки, и также записываются наборы, соответствующие охваченным областям (таблица 1.15).
Чтобы получить минимальную КНФ в карте Карно аналогичными прямоугольными областями охватываются нулевые клетки, и также записываются наборы, соответствующие охваченным областям (таблица 1.15).
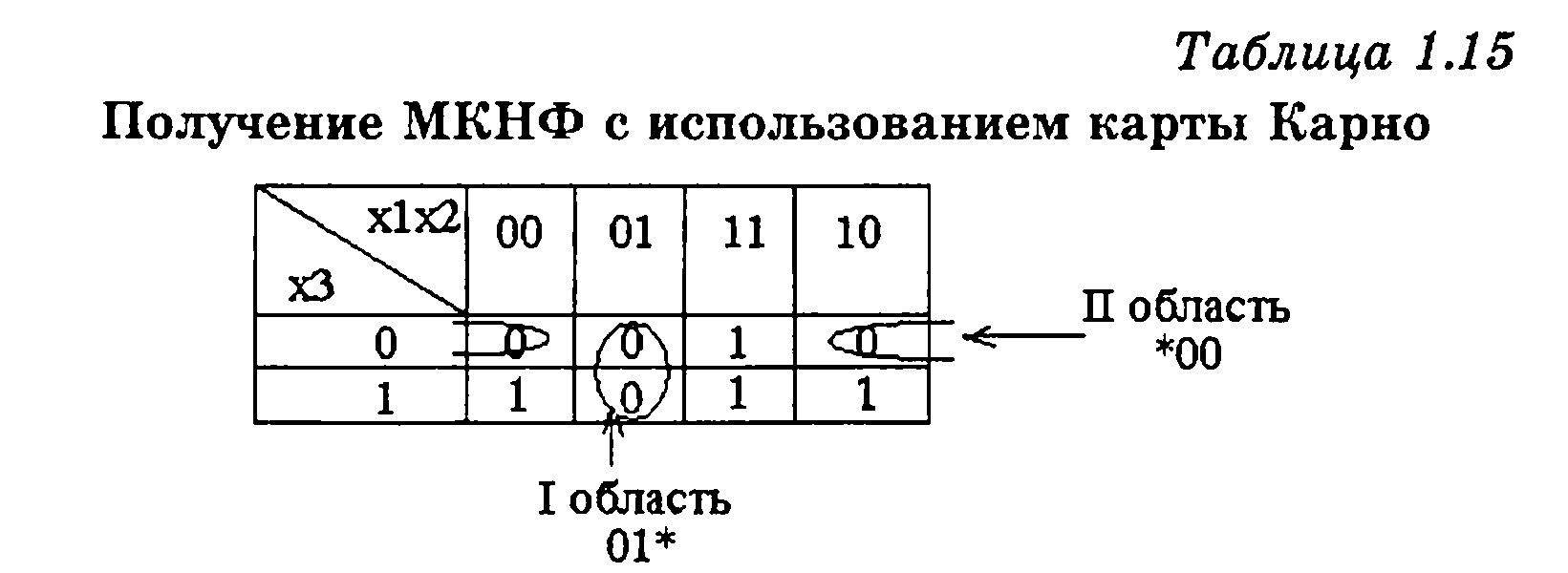
Для получения дизъюнкций, составляющих МКНФ, переменные обозначают через инверсии наборов областей. Первой области соответствует набор 01*, дизъюнкция
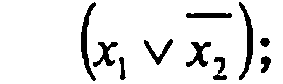 второй области — набор *00, дизъюнкция
второй области — набор *00, дизъюнкция 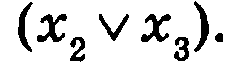 МКНФ функции (таблица 1.15) запишем в виде
МКНФ функции (таблица 1.15) запишем в виде
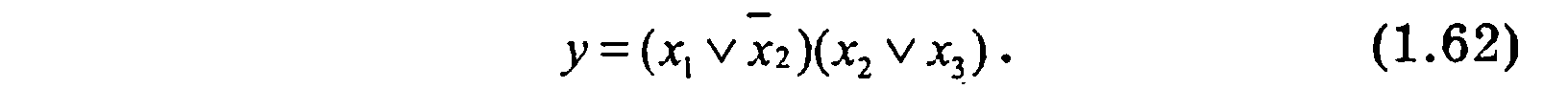 Карты Карно позволяют легко выделить области конъюнкций (либо дизъюнкций), которые подлежат упрощению. Из таблицы 1.15 на примере видно, что карты Карно можно представлять в виде цилиндров по вертикали и горизонтали для выделения единичных либо нулевых областей.
Карты Карно позволяют легко выделить области конъюнкций (либо дизъюнкций), которые подлежат упрощению. Из таблицы 1.15 на примере видно, что карты Карно можно представлять в виде цилиндров по вертикали и горизонтали для выделения единичных либо нулевых областей.
На практике применяют и другие методы минимизации логических функций — метод Петрика, метод карт Вейча. Однако данные методы пригодны для числа переменных до 5. При увеличении числа переменных они становятся громоздкими, теряют наглядность. Кроме того, выбор областей в этих методах в большинстве случаев проводится интуитивно, сильно зависит от индивидуального опыта и искусства разработчика, что препятствует автоматизации проектирования и применения на ЭВМ.
Пример 1[править | править вики-текст]
У мальчика Коли есть мама, папа, дедушка и бабушка. Коля пойдёт гулять на улицу, если и только если ему разрешат хотя бы двое родственников.
Для краткости обозначим родственников Коли через буквы:
мама — х1
папа — х2
дедушка — х3
бабушка — х4
Условимся обозначать согласие родственников единицей, несогласие - нулём. Возможность пойти погулять обозначим буквой f, Коля идёт гулять — f = 1, Коля гулять не идёт — f = 0.
Составим таблицу истинности:

Перерисуем таблицу истинности в 2-х мерный вид:
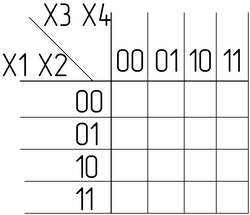
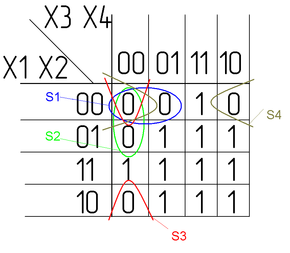
Переставим в ней строки и столбцы в соответствии с кодом Грея. Получили Карту Карно:
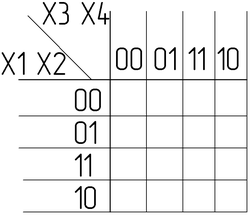
Заполним её значениями из таблицы истинности:
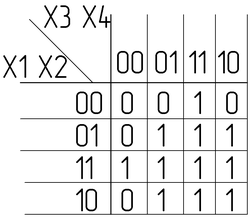
Минимизируем в соответствии с правилами:
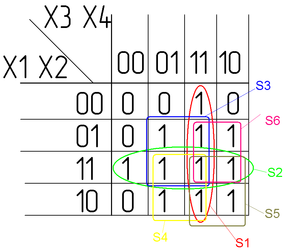
1. 1. Все области содержат 2^n клеток;
2. 2. Так как Карта Карно на четыре переменные, оси располагаются на границах Карты и их не видно (подробнее смотри пример Карты на 5 переменных);
3. 3. Так как Карта Карно на четыре переменные, все области симметрично осей — смежные между собой (подробнее смотри пример Карты на 5 переменных);
4. 4. Области S3, S4, S5, S6 максимально большие;
5. 5. Все области пересекаются (необязательное условие);
6. 6. В данном случае рациональный вариант только один.
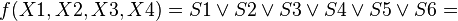
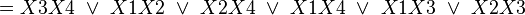
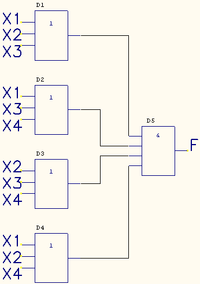
Теперь по полученной минимальной ДНФ можно построить логическую схему:
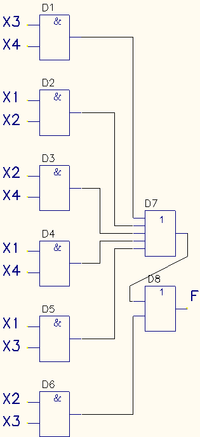
Из-за отсутствия в наличии шести-входового элемента ИЛИ, реализующего функцию дизъюнкции, пришлось каскадировать пяти- и двух-входовые элементы(D7, D8).
Составим мин. КНФ:
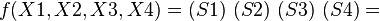
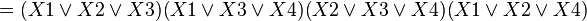
Дата добавления: 2015-09-29; просмотров: 4800;
