Дробная часть

1. Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.

2. Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.

1.Перевод из десятичной в двоичную систему исчисления:

2001,1002₁₀= 11111010001,00011₂

2001 2

2000 1000 2

1 1000 500 2

0 500 250 2

0 250 125 2

0 124 62 2

1 62 31 2

0 30 15 2

1 14 7 2

1 6 3 2

1 2 1

для дробной части:1

0, 1002 *2

0 2004

0 4008

0 8016

1 6032

1 2064

0 4128

0 8256

1 6312

Проверка:

для целой части:

1024;512;256;128;64;32;16;8;4;2;1.

1 1 1 1 1 0 1 0 0 0 1=2001

для дробной части:

1/2;1/4;1/8;1/16;1/32;1/64;1/128;1/256

0 0 0 1 1 0 0 1=1/16+1/32+1/256=25/256≈0,0977

погрешность для дробной части:

0,1002-0,0977=0,0025 - абсолютная погрешность.

0,0025/0,1002*100%≈2,5%- относительная погрешность.

2.Перевод из десятичной в восьмеричную систему исчисления:

2001,1002₁₀=3721,0632326₈

для целой части:

2001 8

2000 250 8

1 248 31 8

2 24 3

для дробной части:

0, 1002 *8

0 8016

6 4128

3 3024

2 4192

3 3536

2 8288

6 6304

Проверка:

для целой части:

a₀=1; a₁=2; a₂=7; a₃=3; q=8.

a₀*q⁰+a₁*q¹+a₂*q²+a₃*q³=1*1+2*8+7*64+3*512=2001.

для дробной части:

a_-1=0; a_-2=6; a_-3=3; a_-4=2; a_-5=3; a_-6=2; a_-7=6; q=8.

a_-1*q^-1+a_-2*q^-2+a_-3*q^-3+a_-4*q^-4 +a_-5*q^-5+a_-6*q^-6+a_-7*q^-7= 0*1/8+ +6*1/64+3*1/512++2*1/4096+3*1/32768+2*1/262144+6*1/2097152≈0,1002

3.Перевод из десятичной в шестнадцатеричную систему исчисления:

2001,1002₁₀=7D1,19A6B5₁₆

для целой части:

2001 16

2000 125 16

1 112

D 7

для дробной части:

0, 1002 *16

1 6032

9 6512

A 4195

6 7072

B 3152

5 0432

0 6912

Проверка:

для целой части:

a₀=1; a₁=13; a₂=7; q=16.

a₀*q⁰+a₁*q¹+a₂*q²=1*1+13*16+7*256=2001.

для дробной части:

a_-1=1; a_-2=9; a_-3=A; a_-4=6; a_-5=B; a_-6=5; q=16.

a_-1*q^-1+a_-2*q^-2+a_-3*q^-3+a_-4*q^-4 +a_-5*q^-5+a_-6*q^-6= 1*1/16+9*1/256+

+10*1/4096+6*1/65536+11*1/1048576+5*1/16777216≈0,1001

погрешность для дробной части:

0,1002-0,1001=0,0001– абсолютная погрешность.

0,0001/0,1002*100%=0,1%– относительная погрешность.

Таблица 1. Степени числа 2

n (степень)

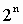
Таблица 2. Степени числа 8

n (степень)

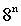
Таблица 3. Степени числа 16

n (степень)

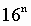
Таблица соответствия между системами счисления

Примеры сложения чисел в двоичной системе исчисления.

Следует обратить внимание на аналогию в правилах выполнения арифметических действий в двоичной и десятичной системах счисления: например, если при сложении двух двоичных чисел сумма цифр окажется больше единицы, то возникает перенос в старший разряд.
Вычитание двоичных чисел осуществляется следующим образом: Вычитаемое число преобразуется в дополнительный код. Например, если надо вычесть из числа 10110 число 01000, то вычитаемое 01000 преобразуется в дополнительный код так: в числе вместо 0 пишется 1, а вместо 1 пишется 0, следовательно, получим из вычитаемого число 10111. Затем преобразованное число складывается с уменьшаемым:

И вычитаемое, и уменьшаемое состоят из 5 разрядов, а результат суммы - число 6-разрядное. Старший разряд суммы отнимается от числа и складывается с результатом:


Такой приём часто используется в практике вычислений. Например, в десятичной системе числа можно вычесть так. Допустим требуется найти разность 842-623. Представим число 623 в дополнительный вид, отняв его от 1000. Получим число 377. Затем найдём сумму: 842+377=1219. Отбросим перенос в старший разряд и получим число 219. Мы нашли решение этого примера.

Деление двоичных чисел выполняется аналогично делению десятичных чисел. Вычитание и умножение в процессе деления необходимо выполнять рассмотренными ранее способами.

Важнейшее преимущество двоичной арифметики заключается в том, что она позволяет все арифметические действия свести к одному - сложению, а это значительно упрощает устройство процессора ЭВМ. Отметим недостаток, характерный для двоичной системы счисления - значительный рост числа разрядов при увеличении числа. Но все достоинства этой системы делают такой недостаток не столь существенным.

Рассмотрим, как выполняются арифметические действия в двоичной системе. Для этого проведём анализ таблиц сложения и умножения в двоичной системе. 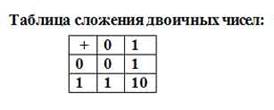Примеры сложения двоичных чисел:

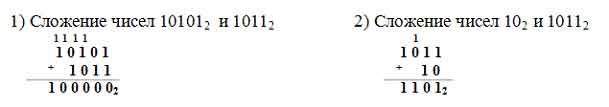
Следует обратить внимание на аналогию в правилах выполнения   арифметических действий в двоичной и десятичной системах счисления: например, если при сложении двух двоичных чисел сумма цифр окажется больше единицы, то возникает перенос в старший разряд. Вычитание двоичных чисел осуществляется следующим образом: Вычитаемое число преобразуется в дополнительный код. Например, если надо вычесть из числа 10110 число 01000, то вычитаемое 01000 преобразуется в дополнительный код так: в числе вместо 0 пишется 1, а вместо 1 пишется 0, следовательно, получим из вычитаемого число 10111. Затем преобразованное число складывается с уменьшаемым: 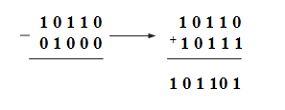И вычитаемое, и уменьшаемое состоят из 5 разрядов, а результат суммы - число 6-разрядное. Старший разряд суммы отнимается от числа и складывается с результатом: Такой приём часто используется в практике вычислений. Например, в десятичной системе числа можно вычесть так. Допустим требуется найти разность 842-623. Представим число 623 в дополнительный вид, отняв его от 1000. Получим число 377. Затем найдём сумму: 842+377=1219. Отбросим перенос в старший разряд и получим число 219. Мы нашли решение этого примера.

3. Задание:

1) Определить типичные характеристики и параметры аппаратных средств персонального компьютера, который установлен на рабочем месте.

2) Определить состав программного обеспечения, которое установлено на компьютере: тип операционной системы, пользователя компьютера, имя компьютера в сети и название домена, в котором находится компьютер, состав и название программ из раздела «Служебные».

3) Провести классификацию программного обеспечения, установленного на данном рабочем месте.

4) Провести кодирование информации.