Закон всемирного тяготения и задача двух тел
Из закона всемирного тяготения вытекают, как следствия, все три закона Кеплера, которые И. Ньютон вывел математически в более общем виде, применимом не только к обращению планет вокруг Солнца, но и к любым системам обращающихся тел.
Задача определения орбиты одного небесного тела относительно другого называется задачей двух тел. При решении этой задачи небесное тело большей массы 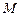 , называемое центральным телом, полагается неподвижным, и определяется орбита, по которой тело меньшей массы
, называемое центральным телом, полагается неподвижным, и определяется орбита, по которой тело меньшей массы 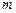 движется относительно центрального тела. Ньютон показал, что в поле тяготения центрального тела любое другое небесное тело будет двигаться по одному из конических сечений – кругу, эллипсу, параболе или гиперболе, причем центральное тело всегда находится в одном из фокусов орбиты движущегося тела, линейная скорость
движется относительно центрального тела. Ньютон показал, что в поле тяготения центрального тела любое другое небесное тело будет двигаться по одному из конических сечений – кругу, эллипсу, параболе или гиперболе, причем центральное тело всегда находится в одном из фокусов орбиты движущегося тела, линейная скорость 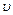 которого относительно центрального на данном расстоянии
которого относительно центрального на данном расстоянии 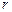 определяется интегралом энергии
определяется интегралом энергии
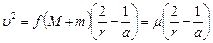 , ,
| (8.1) |
где 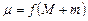 ,
, 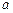 – большая полуось орбиты,
– большая полуось орбиты, 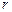 – радиус-вектор движущегося тела,
– радиус-вектор движущегося тела,  – гравитационная постоянная.
– гравитационная постоянная.
Согласно интегралу энергии, каждому расстоянию 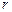 от центрального тела соответствует ряд значений скорости
от центрального тела соответствует ряд значений скорости 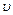 , определяющих род орбиты движущегося тела. Так, чтобы небесное тело обращалось вокруг центрального по круговой орбите радиуса
, определяющих род орбиты движущегося тела. Так, чтобы небесное тело обращалось вокруг центрального по круговой орбите радиуса 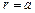 , оно должно на данном расстоянии
, оно должно на данном расстоянии 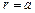 обязательно иметь величину орбитальной скорости
обязательно иметь величину орбитальной скорости 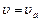 , причем согласно выражению (8.1),
, причем согласно выражению (8.1),
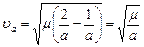
| (8.2) |
или
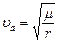 . .
| (8.3) |
Эта скорость называется круговой скоростью.
Если на расстоянии 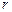 от центрального тела скорость
от центрального тела скорость 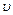 движущегося тела несколько превышает
движущегося тела несколько превышает 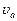 , соответствующую расстоянию
, соответствующую расстоянию 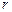 , такое тело также будет спутником центрального, и будет двигаться вокруг него по эллиптической орбите, большая полуось которой
, такое тело также будет спутником центрального, и будет двигаться вокруг него по эллиптической орбите, большая полуось которой 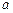 может быть вычислена по интегралу энергии. Чем больше
может быть вычислена по интегралу энергии. Чем больше 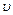 превышает
превышает 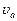 , тем более вытянутой будет эллиптическая орбита (0<e<1). Наконец, если на данном расстоянии
, тем более вытянутой будет эллиптическая орбита (0<e<1). Наконец, если на данном расстоянии 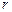 от центрального тела скорость движущегося тела
от центрального тела скорость движущегося тела
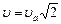 , ,
| (8.4) |
то оно уже не будет спутником центрального тела, а пройдет мимо него по параболической орбите. В самом деле, при подстановке
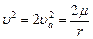
|
в интеграл энергии получим 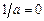 , то есть
, то есть 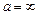 , что характеризует эллиптическую орбиту (e = 1). Поэтому скорость
, что характеризует эллиптическую орбиту (e = 1). Поэтому скорость
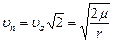
| (8.5) |
называется параболической скоростью.
При 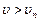 движение тела происходит по гиперболе (
движение тела происходит по гиперболе ( 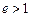 ).
).
При вычислении тех или иных величин приходится пользоваться самыми различными единицами измерений. Так, расстояние между небесными телами выражаются и в километрах (  ) и в астрономических единицах (
) и в астрономических единицах ( 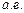 ), массы небесных тел – в массах Земли, массах Солнца, а иногда и в граммах (
), массы небесных тел – в массах Земли, массах Солнца, а иногда и в граммах ( 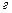 ), время – в годах, средних солнечных сутках и в секундах, линейная скорость, как правило, – в
), время – в годах, средних солнечных сутках и в секундах, линейная скорость, как правило, – в  и так далее. Однако, это отнюдь не означает, что при решении задач можно пользоваться произвольными единицами измерений – все зависит от условий решаемой задачи. Если однородные физические величины входят в уравнение в виде отношения, то они могут быть выражены в любых соответствующих, но обязательно одинаковых единицах измерения, вне зависимости от единиц измерения других величин, входящих в то же уравнение. Если же уравнением связаны разнородные физические величины, то все они должны быть выражены обязательно в одной определенной системе единиц.
и так далее. Однако, это отнюдь не означает, что при решении задач можно пользоваться произвольными единицами измерений – все зависит от условий решаемой задачи. Если однородные физические величины входят в уравнение в виде отношения, то они могут быть выражены в любых соответствующих, но обязательно одинаковых единицах измерения, вне зависимости от единиц измерения других величин, входящих в то же уравнение. Если же уравнением связаны разнородные физические величины, то все они должны быть выражены обязательно в одной определенной системе единиц.
Часто приходится применять абсолютную систему единиц СГС, в которой масса выражается в граммах ( 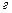 ), расстояние – в сантиметрах (
), расстояние – в сантиметрах ( 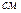 ), время – в секундах (
), время – в секундах ( 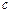 ), скорость – в
), скорость – в 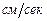 , ускорение – в
, ускорение – в 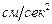 , тогда гравитационная константа
, тогда гравитационная константа 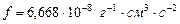 . В Международной системе единиц СИ, практически не используемой в астрономии, масса выражается в
. В Международной системе единиц СИ, практически не используемой в астрономии, масса выражается в 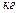 , расстояние – в метрах (
, расстояние – в метрах (  ), время – в секундах (
), время – в секундах ( 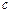 ), скорость – в
), скорость – в  и
и 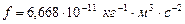 .
.
Следует предупредить о бессмысленном вычислении масс небесных тел с точностью до 1 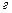 или 1
или 1 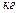 , а расстояний – с точностью 1
, а расстояний – с точностью 1 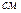 или 1
или 1  ; речь идет лишь об их выражении в системе СГС или СИ, и поэтому при вычислениях достаточно ограничиться числом из трех-четырех значащих цифр, умножая его на число 10 в определенной степени
; речь идет лишь об их выражении в системе СГС или СИ, и поэтому при вычислениях достаточно ограничиться числом из трех-четырех значащих цифр, умножая его на число 10 в определенной степени  (то есть
(то есть 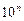 ), полученной при вычислениях.
), полученной при вычислениях.
В астрономии часто применяется гауссова система единиц, в которой массы небесных тел выражаются в массах Солнца, единицей длины является астрономическая единица ( 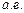 ), а единицей времени – средние солнечные сутки.
), а единицей времени – средние солнечные сутки.
Если же массы небесных тел выражать в солнечных массах, расстояния – в астрономических единицах, а скорость – в  , то
, то 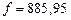 и
и 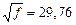 .
.
Полагая в равенстве (8.1) массу Солнца  и пренебрегая в сравнении с массой Солнца малыми массами его спутников (
и пренебрегая в сравнении с массой Солнца малыми массами его спутников ( 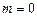 ), получим
), получим 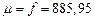 , и тогда скорость небесных тел в поле тяготения Солнца определится как
, и тогда скорость небесных тел в поле тяготения Солнца определится как
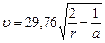 , ,
| (8.6) |
где 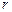 и
и 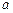 выражены в астрономических единицах (
выражены в астрономических единицах ( 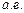 ), а
), а 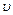 в
в  .
.
Выражение (8.6) позволяет вычислить скорость планет и комет на любом расстоянии 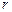 от Солнца. Положив в формуле (8.6)
от Солнца. Положив в формуле (8.6) 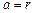 , можно найти значение круговой скорости
, можно найти значение круговой скорости
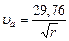
| (8.7) |
и значение параболической скорости 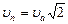 на произвольном расстоянии
на произвольном расстоянии 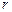 от Солнца.
от Солнца.
При подстановке в равенство (8.7) 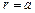 и делении на него выражения (8.6), получается удобная формула для вычисления скорости
и делении на него выражения (8.6), получается удобная формула для вычисления скорости 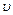 тел в поле тяготения Солнца по их круговой скорости
тел в поле тяготения Солнца по их круговой скорости 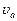 .
.
Из интеграла энергии (8.1) весьма просто выводится третий закон Кеплера в обобщенном виде, для чего достаточно эллиптическое движение спутника заменить движением по круговой орбите радиуса 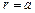 . Тогда круговая скорость спутника
. Тогда круговая скорость спутника
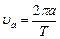 , ,
| (8.8) |
где 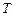 – период обращения спутника вокруг центрального тела, а так как, согласно формуле (8.2),
– период обращения спутника вокруг центрального тела, а так как, согласно формуле (8.2),
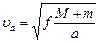 , то , то
| |
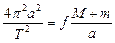 , откуда , откуда
| |
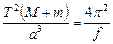 . .
| (8.9) |
Массы 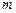 спутников, как правило, очень малы в сравнении с массой
спутников, как правило, очень малы в сравнении с массой 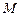 центрального тела, и поэтому, пренебрегая в формуле (8.9) величиной
центрального тела, и поэтому, пренебрегая в формуле (8.9) величиной 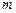 , можно вычислить массу центрального тела в определенной системе единиц.
, можно вычислить массу центрального тела в определенной системе единиц.
Поскольку масса небесных тел обычно вычисляется в сравнении с солнечной или земной массой (то есть, в массах Солнца или в массах Земли), то значительно проще применить третий обобщенный закон Кеплера к двум системам обращающихся тел
 . .
| (8.10) |
Здесь величины с индексом 1 относятся к одной системе центрального тела и его спутника, а те же величины с индексом 2 – к другой системе аналогичных тел.
При определении масс планет в массах Земли сравнивают движение спутника планеты с движением Луны вокруг Земли. Для этого в формуле (8.10) под  подразумевают массу планеты, под
подразумевают массу планеты, под 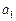 и
и 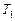 – большую полуось орбиты спутника и период его обращения вокруг планеты, а массой спутника
– большую полуось орбиты спутника и период его обращения вокруг планеты, а массой спутника 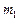 пренебрегают (
пренебрегают ( 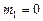 ). Считая
). Считая 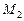 массой Земли,
массой Земли, 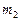 – массой Луны,
– массой Луны, 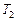 – звездным месяцем и
– звездным месяцем и 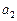 – большой полуосью лунной орбиты, вычисляют массу планеты
– большой полуосью лунной орбиты, вычисляют массу планеты  в массах Земли и Луны
в массах Земли и Луны 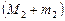 , а затем уже, зная, что масса Луны (
, а затем уже, зная, что масса Луны ( 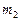 ) в 81,3 раза меньше массы Земли (
) в 81,3 раза меньше массы Земли ( 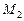 ), находят массу планеты
), находят массу планеты  в массах Земли
в массах Земли 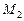 .
.
Зная массу 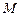 и радиус
и радиус 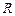 небесного тела, можно вычислить ускорение силы тяжести
небесного тела, можно вычислить ускорение силы тяжести 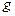 на его поверхности, причем удобнее всего вычислять
на его поверхности, причем удобнее всего вычислять 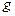 в сравнении с ускорением
в сравнении с ускорением 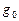 на Земле, а затем уже, в случае необходимости, найти его абсолютное значение. Очевидно, на поверхности небесного тела
на Земле, а затем уже, в случае необходимости, найти его абсолютное значение. Очевидно, на поверхности небесного тела
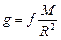 , ,
| (8.11) |
а на земной поверхности
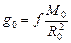
| (8.12) |
и тогда
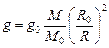
|
или
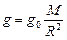 , ,
| (8.13) |
где 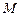 выражена в массах Земли, а
выражена в массах Земли, а 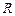 – в радиусах Земли.
– в радиусах Земли.
Аналогичным образом вычисляется гравитационное ускорение  небесных тел в поле тяготения центрального тела на расстоянии
небесных тел в поле тяготения центрального тела на расстоянии 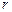 от него
от него
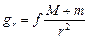
| (8.14) |
или
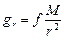 , ,
| (8.15) |
если 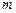 мало в сравнении с
мало в сравнении с 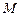 .
.
Формула (8.15) позволяет также вычислить массу центрального тела по известному гравитационному ускорению  .
.
Разделив равенство (8.15) на выражение (8.11), получим для вычисления  простую формулу, в которой
простую формулу, в которой 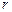 выражается в радиусах
выражается в радиусах 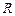 небесного тела.
небесного тела.
Задания:
1. По движению Луны вокруг Земли определить массу Земли в системе СГС.
2. Вычислить круговую, параболическую и действительную скорости на среднем, перигелийном и афелийном расстояниях малой планеты: 1) Психеи; 2) Андромахи; 3) Эскулапии; 4) Урании; 4) Галатеи; 5) Глазенапии; 6) Полигимнии; 7) Фотографики.
3. Из сопоставления вычисленных в пункте 2 скоростей сформулировать вывод о признаках, характерных для движения тел по эллиптической орбите.
4. Определить в массах Земли массу Солнца и планеты: 1) Марса (по движению Фобоса); 2) Юпитера (по движению Ио); 3) Сатурна (по движению Титана); 4) Урана (по движению Ариэля); 5) Нептуна (по движению Тритона); 6) Марса (по движению Деймоса); 7) Юпитера (по движению Европы); 8) Сатурна (по движению Япета).
5. Определить ускорение силы тяжести на поверхности Солнца, Луны и той же планеты.
6. Вычислить свой вес на поверхности тех же небесных тел.
7. Вычислить вес космического корабля-спутника «Восток» на поверхности Луны и той же планеты (вес этого корабля на Земле равен 47 кН).
8. Определить ускорение силы тяжести на расстояниях, равных одному, четырем и девяти радиусам от поверхности тех же небесных тел.
9. Вычислить гравитационное ускорение Земли и той же планеты в поле тяготения Солнца.
10. Из анализа результатов пунктов 5-9 сформулировать выводы о причинах различия гравитационного ускорения в поле тяготения разных тел и графически изобразить зависимость гравитационного ускорения от соответствующих аргументов.
11. Вычислить ускорение силы тяжести на поверхности Солнца, луны и той же планеты при условии увеличения их диаметров вдвое и при сохранении их средней плотности неизменной.
12. Определить гипотетическую массу Земли, при которой Луна обращалась бы вокруг нее с современным периодом, но на вдвое большем расстоянии, и сравнить гравитационное ускорение Луны в этом случае с действительным его значением.
13. Вычислить гипотетическую массу Солнца, при которой та же планета, сохраняя свою орбитальную скорость, перестала бы быть его спутником.
Дата добавления: 2015-09-29; просмотров: 1523;
