Видимое годовое движение Солнца
Вследствие годового обращения Земли вокруг Солнца в направлении с запада на восток нам кажется, что Солнце перемещается среди звезд с запада к востоку по большому кругу небесной сферы, который называется эклиптикой, с периодом 1 год. Плоскость эклиптики (плоскость земной орбиты) наклонена к плоскости небесного (а также земного) экватора под углом 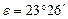 . Этот угол называют наклонением эклиптики.
. Этот угол называют наклонением эклиптики.
Положение эклиптики на небесной сфере, то есть экваториальные координаты 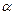 и
и  точек эклиптики и ее наклонение
точек эклиптики и ее наклонение 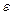 к небесному экватору определяются из ежедневных наблюдений Солнца. Измеряя зенитное расстояние (или высоту) Солнца в момент его верхней кульминации на одной и той же географической широте,
к небесному экватору определяются из ежедневных наблюдений Солнца. Измеряя зенитное расстояние (или высоту) Солнца в момент его верхней кульминации на одной и той же географической широте,
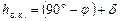 , ,
| (6.1) |
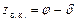 , ,
| (6.2) |
можно установить, что склонение Солнца в течение года изменяется в пределах от 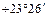 до
до 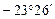 . При этом прямое восхождение Солнца на протяжении года изменяется от
. При этом прямое восхождение Солнца на протяжении года изменяется от 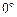 до
до 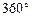 , или от
, или от 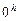 до
до 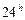 .
.
Рассмотрим подробнее изменение координат Солнца.
В точке весеннего равноденствия ^, которую Солнце проходит ежегодно 21 марта, прямое восхождение и склонение Солнца раны нулю. Затем с каждым днем прямое восхождение и склонение Солнца увеличиваются.
В точке летнего солнцестояния a, в которую Солнце попадает 22 июня, его прямое восхождение равно 6h, а склонение достигает максимального значения + 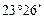 . После этого склонение Солнца уменьшается, а прямое восхождение по-прежнему растет.
. После этого склонение Солнца уменьшается, а прямое восхождение по-прежнему растет.
Когда Солнце 23 сентября приходит в точку осеннего равноденствия d, его прямое восхождение 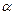 станет равным
станет равным 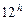 , а склонение
, а склонение  снова станет равно нулю.
снова станет равно нулю.
Далее, прямое восхождение, продолжая увеличиваться, в точке зимнего солнцестояния g, куда Солнце попадает 22 декабря, становится равным 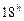 , а склонение достигает своего минимального значения -
, а склонение достигает своего минимального значения - 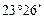 . После этого склонение возрастает, и Солнце через три месяца приходит вновь в точку весеннего равноденствия.
. После этого склонение возрастает, и Солнце через три месяца приходит вновь в точку весеннего равноденствия.
Рассмотрим изменение местоположения Солнца на небе в течение года для наблюдателей, находящихся в разных местах на поверхности Земли.
Для наблюдателя находящегося на северном полюсе Земли 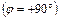 , в день весеннего равноденствия (21.03) Солнце совершает круг по горизонту. (Напомним, что на Северном полюсе земли не существует явлений восхода и захода светил, то есть любое светило движется параллельно горизонту, не пересекая его). Это знаменует начало полярного дня на Северном полюсе. На следующий день Солнце, чуть-чуть поднявшись по эклиптике, опишет круг, параллельный горизонту, на немного большей высоте. С каждым днем оно будет подниматься все выше и выше. Максимальной высоты Солнце достигнет в день летнего солнцестояния (22.06) –
, в день весеннего равноденствия (21.03) Солнце совершает круг по горизонту. (Напомним, что на Северном полюсе земли не существует явлений восхода и захода светил, то есть любое светило движется параллельно горизонту, не пересекая его). Это знаменует начало полярного дня на Северном полюсе. На следующий день Солнце, чуть-чуть поднявшись по эклиптике, опишет круг, параллельный горизонту, на немного большей высоте. С каждым днем оно будет подниматься все выше и выше. Максимальной высоты Солнце достигнет в день летнего солнцестояния (22.06) – 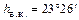 . После этого начнется медленное уменьшение высоты. В день осеннего равноденствия (23.09) Солнце опять окажется на небесном экваторе, который совпадает с горизонтом на Северном полюсе. Совершив прощальный круг вдоль горизонта в этот день, Солнце на полгода опускается под горизонт (под небесный экватор). Длившийся полгода полярный день завершен. Начинается полярная ночь.
. После этого начнется медленное уменьшение высоты. В день осеннего равноденствия (23.09) Солнце опять окажется на небесном экваторе, который совпадает с горизонтом на Северном полюсе. Совершив прощальный круг вдоль горизонта в этот день, Солнце на полгода опускается под горизонт (под небесный экватор). Длившийся полгода полярный день завершен. Начинается полярная ночь.
Для наблюдателя находящегося на северном полярном круге 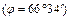 наибольшей высоты Солнце достигает в полдень в день летнего солнцестояния –
наибольшей высоты Солнце достигает в полдень в день летнего солнцестояния – 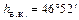 . Полуночная высота Солнца в этот день равна 0°, то есть Солнце в этот день не заходит. Такое явление принято называть полярным днем.
. Полуночная высота Солнца в этот день равна 0°, то есть Солнце в этот день не заходит. Такое явление принято называть полярным днем.
В день зимнего солнцестояния его полуденная высота минимальна – 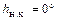 , то есть Солнце не восходит. Это называется полярная ночь. Широта северного полярного круга – наименьшая в северном полушарии Земли, где наблюдаются явления полярных дня и ночи.
, то есть Солнце не восходит. Это называется полярная ночь. Широта северного полярного круга – наименьшая в северном полушарии Земли, где наблюдаются явления полярных дня и ночи.
Для наблюдателя находящегося на северном тропике 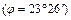 , Солнце каждый день восходит и заходит. Максимальной полуденной высоты над горизонтом Солнце достигает в день летнего солнцестояния – в этот день оно проходит точку зенита (
, Солнце каждый день восходит и заходит. Максимальной полуденной высоты над горизонтом Солнце достигает в день летнего солнцестояния – в этот день оно проходит точку зенита ( 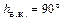 ). Северный тропик – самая северная параллель, где Солнце бывает в зените. Минимальная полуденная высота,
). Северный тропик – самая северная параллель, где Солнце бывает в зените. Минимальная полуденная высота, 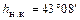 , наблюдается в день зимнего солнцестояния.
, наблюдается в день зимнего солнцестояния.
Для наблюдателя находящегося на экваторе 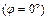 , абсолютно все светила заходят и восходят. При этом любое светило, в том числе и Солнце, ровно 12 часов проводят над горизонтом и 12 часов – под горизонтом. Это значит, что продолжительность дня всегда равна продолжительности ночи – по 12 часов. Дважды в году – в дни равноденствий – полуденная высота Солнца становится 90°, то есть проходит через точку зенита.
, абсолютно все светила заходят и восходят. При этом любое светило, в том числе и Солнце, ровно 12 часов проводят над горизонтом и 12 часов – под горизонтом. Это значит, что продолжительность дня всегда равна продолжительности ночи – по 12 часов. Дважды в году – в дни равноденствий – полуденная высота Солнца становится 90°, то есть проходит через точку зенита.
Для наблюдателя находящегося на широте Стерлитамака 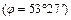 , то есть в умеренном поясе, Солнце никогда не бывает в зените. Наибольшей высоты достигает в полдень 22 июня, в день летнего солнцестояния, –
, то есть в умеренном поясе, Солнце никогда не бывает в зените. Наибольшей высоты достигает в полдень 22 июня, в день летнего солнцестояния, – 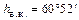 . В день зимнего солнцестояния, 22 декабря, его высота минимальна –
. В день зимнего солнцестояния, 22 декабря, его высота минимальна – 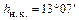 .
.
Итак, сформулируем следующие астрономические признаки тепловых поясов:
1. В холодных поясах (от полярных кругов 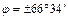 до полюсов Земли
до полюсов Земли 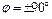 ) Солнце может быть и незаходящим, и невосходящим светилом. Полярный день и полярная ночь могут длиться от 24 часов (на северном и южном полярных кругах) до полугода (на северном и южном полюсах Земли).
) Солнце может быть и незаходящим, и невосходящим светилом. Полярный день и полярная ночь могут длиться от 24 часов (на северном и южном полярных кругах) до полугода (на северном и южном полюсах Земли).
2. В умеренных поясах (от северного и южного тропиков 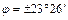 до северного и южного полярных кругов
до северного и южного полярных кругов 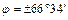 ) Солнце каждый день восходит и заходит, но никогда не бывает в зените. Летом день длиннее ночи, а зимой – наоборот.
) Солнце каждый день восходит и заходит, но никогда не бывает в зените. Летом день длиннее ночи, а зимой – наоборот.
3. В жарком поясе (от северного тропика 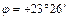 до южного тропика
до южного тропика 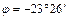 ) Солнце всегда восходящее и заходящее. В зените Солнце бывает от одного раза – на северном и южном тропиках, до двух раз – на других широтах пояса.
) Солнце всегда восходящее и заходящее. В зените Солнце бывает от одного раза – на северном и южном тропиках, до двух раз – на других широтах пояса.
Регулярная смена времен года на Земле является следствием трех причин: годового обращения Земли вокруг Солнца, наклона земной оси к плоскости земной орбиты (плоскости эклиптики) и сохранения земной осью своего направления в пространстве на протяжении длительных промежутков времени. Благодаря совместному действию этих трех причин происходит видимое годовое движение Солнца по эклиптике, наклоненной к небесному экватору, и поэтому положение суточного пути Солнца над горизонтом различных мест земной поверхности на протяжении года изменяется, а следовательно, изменяются условия их освещения и обогревания Солнцем.
Неодинаковое обогревание Солнцем областей земной поверхности с различной географической широтой 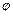 (или этих же областей в разное время года) легко выясняется простым подсчетом. Обозначим через
(или этих же областей в разное время года) легко выясняется простым подсчетом. Обозначим через 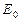 количество тепла, передаваемого единице площади земной поверхности отвесно падающими солнечными лучами (Солнце в зените). Тогда при другом зенитном расстоянии Солнца
количество тепла, передаваемого единице площади земной поверхности отвесно падающими солнечными лучами (Солнце в зените). Тогда при другом зенитном расстоянии Солнца 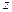 та же единица площади получит количество тепла
та же единица площади получит количество тепла
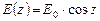
| (6.3) |
Подставляя в эту формулу значения 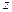 Солнца в истинный полдень разных дней года и деля полученные равенства друг на друга, можно найти отношение количества тепла, получаемого от Солнца в полдень в эти дни года.
Солнца в истинный полдень разных дней года и деля полученные равенства друг на друга, можно найти отношение количества тепла, получаемого от Солнца в полдень в эти дни года.
Задания:
1. Вычислить наклонение эклиптики и определить экваториальные и эклиптические координаты ее основных точек по измеренному зенитному расстоянии. Солнца в верхней кульминации в дни солнцестояний:
| № | 22 июня | 22 декабря |
| 1) | 29〫48ʹ ю | 76〫42ʹ ю |
| № | 22 июня | 22 декабря |
| 2) | 19〫23ʹ ю | 66〫17ʹ ю |
| 3) | 34〫57ʹ ю | 81〫51ʹ ю |
| 4) | 32〫21ʹ ю | 79〫15ʹ ю |
| 5) | 14〫18ʹ ю | 61〫12ʹ ю |
| 6) | 28〫12ʹ ю | 75〫06ʹ ю |
| 7) | 17〫51ʹ ю | 64〫45ʹ ю |
| 8) | 26〫44ʹ ю | 73〫38ʹ ю |
2. Определить наклонение видимого годового пути Солнца к небесному экватору на планетах Марс, Юпитер и Уран.
3. Определить наклонение эклиптики около 3000 лет назад, если по наблюдениям в ту эпоху в некотором месте северного полушария Земли полуденная высота Солнца в день летнего солнцестояния равнялась +63〫48ʹ, а в день зимнего солнцестояния +16〫00ʹ к югу от зенита.
4. По картам звездного атласа академика А.А. Михайлова установить названия и границы зодиакальных созвездий, указать те из них, в которых находятся основные точки эклиптики, и определить среднюю продолжительность перемещения Солнца на фоне каждого зодиакального созвездия.
5. По подвижной карте звездного неба определить азимуты точек и моменты времени восхода и захода Солнца, а также примерную продолжительность дня и ночи на географической широте Стерлитамака в дни равноденствий и солнцестояний.
6. Вычислить для дней равноденствий и солнцестояний полуденную и полуночную высоту Солнца в: 1) Москве; 2) Твери; 3) Казани; 4) Омске; 5) Новосибирске; 6) Смоленске; 7) Красноярске; 8) Волгограде.
7. Вычислить отношения количеств тепла, получаемых в полдень от Солнца в дни солнцестояний одинаковыми площадками в двух пунктах земной поверхности, расположенных на широте: 1) +60〫30ʹ и в Майкопе; 2) +70〫00ʹ и в Грозном; 3) +66〫30ʹ и в Махачкале; 4) +69〫30ʹ и во Владивостоке; 5) +67〫30ʹ и в Махачкале; 6) +67〫00ʹ и в Южно-Курильске; 7) +68〫00ʹ и в Южно-Сахалинске; 8) +69〫00ʹ и в Ростове-на-Дону.
Законы кеплера и конфигурации планет
Под действием гравитационного притяжения к Солнцу планеты обращаются вокруг него по слабовытянутым эллиптическим орбитам. Солнце находится в одном из фокусов эллиптической орбиты планеты. Это движение подчиняется законам Кеплера.
Величина большой полуоси 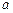 эллиптической орбиты планеты является также средним расстоянием от планеты до Солнца. Благодаря незначительным эксцентриситетам
эллиптической орбиты планеты является также средним расстоянием от планеты до Солнца. Благодаря незначительным эксцентриситетам 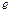 и небольшим наклонениям
и небольшим наклонениям  орбит больших планет, можно при решении многих задач приближенно полагать эти орбиты круговыми с радиусом
орбит больших планет, можно при решении многих задач приближенно полагать эти орбиты круговыми с радиусом 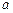 и лежащими практически в одной плоскости – в плоскости эклиптики (плоскости земной орбиты).
и лежащими практически в одной плоскости – в плоскости эклиптики (плоскости земной орбиты).
Согласно третьему закону Кеплера, если 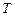 и
и 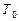 – соответственно звездные (сидерические) периоды обращения некоторой планеты и Земли вокруг Солнца, а
– соответственно звездные (сидерические) периоды обращения некоторой планеты и Земли вокруг Солнца, а 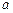 и
и 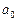 – большие полуоси их орбит, то
– большие полуоси их орбит, то
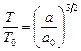 . .
| (7.1) |
Здесь периоды обращения планеты и Земли могут быть выражены в любых единицах, но размерности 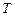 и
и 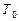 должны быть одинаковы. Подобное утверждение справедливо и для больших полуосей
должны быть одинаковы. Подобное утверждение справедливо и для больших полуосей 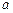 и
и 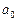 .
.
Если за единицу измерения времени принять 1 тропический год ( 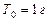 – период обращения Земли вокруг Солнца), а за единицу измерения расстояния 1 астрономическую единицу (
– период обращения Земли вокруг Солнца), а за единицу измерения расстояния 1 астрономическую единицу ( 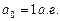 ), то третий закон Кеплера (7.1) можно переписать в виде
), то третий закон Кеплера (7.1) можно переписать в виде
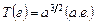 . .
| (7.2) |
Угловая и линейная скорости планеты при ее движении на орбите периодически изменяются в соответствии со вторым законом Кеплера. Их средние значения могут быть посчитаны по средней удаленности 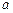 планеты от Солнца.
планеты от Солнца.
Средняя суточная угловая скорость планеты, определяется выражением
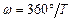 , ,
| (7.3) |
где 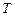 – сидерический период обращения планеты вокруг Солнца, выраженный в средних солнечных сутках.
– сидерический период обращения планеты вокруг Солнца, выраженный в средних солнечных сутках.
Очевидно, для Земли средняя угловая скорость определяется формулой
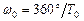
| (7.4) |
и составляет 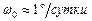 .
.
Поделив (7.3) на (7.4), получим
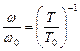 . .
| (7.5) |
Если принять за единицу измерения угловых скоростей планеты и Земли 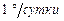 , а периоды обращения измерять в тропических годах, то формула (7.5) может быть записана в виде
, а периоды обращения измерять в тропических годах, то формула (7.5) может быть записана в виде
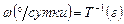 . .
| (7.6) |
Учтя третий закон Кеплера (7.2), запишем зависимость средней угловой скорости планеты от большой полуоси ее орбиты
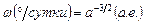 . .
| (7.7) |
Средняя линейная скорость движения планеты на орбите может быть рассчитана по формуле
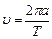 , ,
| (7.8) |
Аналогичная величина для Земли
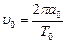 . .
| (7.9) |
Среднее значение орбитальной скорости Земли известно и составляет 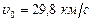 . Поделив (7.8) на (7.9) и используя третий закон Кеплера (7.2), найдем зависимость
. Поделив (7.8) на (7.9) и используя третий закон Кеплера (7.2), найдем зависимость 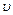 от
от 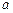
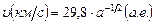 , ,
| (7.10) |
Звездный (сидерический) 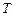 и синодический
и синодический 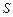 периоды обращения планеты связаны между собой уравнением синодического движения
периоды обращения планеты связаны между собой уравнением синодического движения
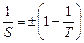 . .
| (7.11) |
Знак «-» соответствует внутренним или нижним планетам (Меркурий, Венера), а «+» – внешним или верхним (Марс, Юпитер, Сатурн, Уран, Нептун). В этой формуле 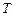 и
и 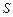 выражены в годах. В случае необходимости найденные значения
выражены в годах. В случае необходимости найденные значения 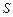 и
и 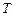 всегда могут быть выражены в сутках.
всегда могут быть выражены в сутках.
Взаимное расположение планет легко устанавливается по их гелиоцентрическим эклиптическим сферическим координатам, значения которых на различные дни года публикуются в астрономических календарях-ежегодниках, в таблице под названием «гелиоцентрические долготы планет».
Центром этой системы координат (рис. 7.1) является центр Солнца, а основным кругом – эклиптика, полюса которой 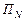 и
и 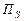 отстоят от нее на 90º.
отстоят от нее на 90º.
Большие круги, проведенные через полюса эклиптики, называются кругами эклиптической широты, по ним отсчитывается от эклиптики гелиоцентрическая эклиптическая широта 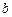 , которая считается положительной в северном эклиптическом полушарии и отрицательной в южном эклиптическом полушарии небесной сферы. Гелиоцентрическая эклиптическая долгота
, которая считается положительной в северном эклиптическом полушарии и отрицательной в южном эклиптическом полушарии небесной сферы. Гелиоцентрическая эклиптическая долгота 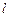 отсчитывается по эклиптике от точки весеннего равноденствия ¡ против часовой стрелки до основания круга широты светила и имеет значения в пределах от 0º до 360º.
отсчитывается по эклиптике от точки весеннего равноденствия ¡ против часовой стрелки до основания круга широты светила и имеет значения в пределах от 0º до 360º.
Из-за малого наклонения орбит больших планет к плоскости эклиптики, эти орбиты всегда находятся вблизи эклиптики, и в первом приближении можно считать их гелиоцентрическую долготу 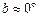 , определяя положение планеты относительно Солнца лишь одной ее гелиоцентрической эклиптической долготой
, определяя положение планеты относительно Солнца лишь одной ее гелиоцентрической эклиптической долготой 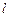 .
.

Рис. 7.1. Эклиптическая система небесных координат
Рассмотрим орбиты Земли и некоторой внутренней планеты (рис. 7.2), используя гелиоцентрическую эклиптическую систему координат. В ней основным кругом является эклиптика, а нуль-пунктом – точка весеннего равноденствия ^. Отсчет эклиптической гелиоцентрической долготы планеты ведется от направления «Солнце – точка весеннего равноденствия ^» до направления «Солнце – планета» против часовой стрелки. Для простоты будем считать плоскости орбит Земли и планеты совпадающими, а сами орбиты – круговыми. Тогда положение планеты на орбите задается ее эклиптической гелиоцентрической долготой 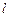 .
.
Если центр эклиптической системы координат совместить с центром Земли, то это будет геоцентрическая эклиптическая система координат. Тогда угол между направлениями «центр Земли – точка весеннего равноденствия ^» и «центр Земли – планета» называется эклиптической геоцентрической долготой планеты 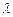 . Гелиоцентрическая эклиптическая долгота Земли
. Гелиоцентрическая эклиптическая долгота Земли 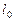 и геоцентрическая эклиптическая долгота Солнца
и геоцентрическая эклиптическая долгота Солнца 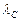 , как видно из рис. 7.2, связаны соотношением:
, как видно из рис. 7.2, связаны соотношением:
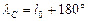 . .
| (7.12) |
Будем называть конфигурацией планеты некоторое фиксированное взаимное расположение планеты, Земли и Солнца.
Рассмотрим раздельно конфигурации внутренних и внешних планет.
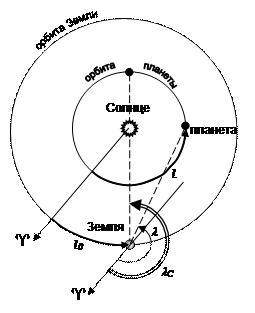
Рис. 7.2. Гелио- и геоцентрическая системы
эклиптических координат
Различают четыре конфигурации внутренних планет: нижнее соединение (н.с.), верхнее соединение (в.с.), наибольшая западная элонгация (н.з.э.) и наибольшая восточная элонгация (н.в.э.).
В нижнем соединении (н.с.) внутренняя планета находится на прямой, соединяющей Солнце и Землю, между Солнцем и Землей (рис. 7.3). Для земного наблюдателя в этот момент внутренняя планета «соединяется» с Солнцем, то есть видна на фоне Солнца. При этом эклиптические геоцентрические долготы Солнца и внутренней планеты равны, то есть: 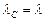 .
.
Вблизи нижнего соединения планета перемещается на небе в попятном движении около Солнца, над горизонтом находится днем, причем около Солнца, и наблюдать ее, разглядывая что-либо на ее поверхности, невозможно. Очень редко удается увидеть уникальное астрономическое явление – прохождение внутренней планеты (Меркурия или Венеры) по диску Солнца.
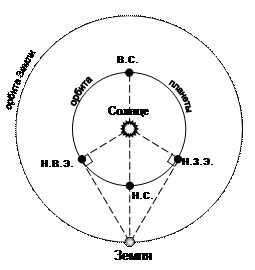
Рис. 7.3. Конфигурации внутренних планет
Так как угловая скорость внутренней планеты больше угловой скорости Земли, через некоторое время планета сместится в положение, где направления «планета-Солнце» и «планета-Земля» отличаются на 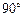 (рис. 7.3). Для земного наблюдателя планета при этом удалена от солнечного диска на максимальный угол, или говорят, что планета в этот момент находится в наибольшей элонгации (удалении от Солнца). Различают две наибольших элонгации внутренней планеты – западную (н.з.э.) и восточную (н.в.э.). В наибольшей западной элонгации
(рис. 7.3). Для земного наблюдателя планета при этом удалена от солнечного диска на максимальный угол, или говорят, что планета в этот момент находится в наибольшей элонгации (удалении от Солнца). Различают две наибольших элонгации внутренней планеты – западную (н.з.э.) и восточную (н.в.э.). В наибольшей западной элонгации 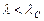 (
( 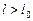 ) и планета заходит за горизонт и восходит раньше, чем Солнце. Это значит, что наблюдать ее можно утром, перед восходом Солнца, в восточной стороне неба. Это называется утренней видимостью планеты.
) и планета заходит за горизонт и восходит раньше, чем Солнце. Это значит, что наблюдать ее можно утром, перед восходом Солнца, в восточной стороне неба. Это называется утренней видимостью планеты.
После прохождения наибольшей западной элонгации диск планеты начинает приближаться на небесной сфере к диску Солнца до тех пор, пока планета не исчезнет за диском Солнца. Эта конфигурация, когда Земля, Солнце и планета лежат на одной прямой, причем планета находится за Солнцем, называется верхним соединением (в.с.) планеты. Проводить в этот момент наблюдения внутренней планеты нельзя.
После верхнего соединения угловое расстояние между планетой и Солнцем начинает расти, достигая максимального значения в наибольшей восточной элонгации (н.в.э.). При этом гелиоцентрическая эклиптическая долгота планеты больше, чем у Солнца 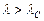 (а геоцентрическая – наоборот, меньше, то есть
(а геоцентрическая – наоборот, меньше, то есть 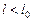 ). Планета в этой конфигурации восходит и заходит позднее Солнца, что дает возможность наблюдать ее вечером после захода Солнца (вечерняя видимость).
). Планета в этой конфигурации восходит и заходит позднее Солнца, что дает возможность наблюдать ее вечером после захода Солнца (вечерняя видимость).
Из-за эллиптичности орбит планет и Земли угол между направлениями на Солнце и на планету в наибольшей элонгации не постоянен, а изменяется в некоторых пределах, для Меркурия – от 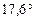 до
до 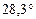 , для Венеры – от
, для Венеры – от 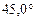 до
до 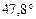 .
.
Наибольшие элонгации – самые удобные моменты для наблюдений внутренних планет. Но так как даже в этих конфигурациях Меркурий и Венера не отходят на небесной сфере далеко от Солнца, наблюдать их в течение всей ночи нельзя. Продолжительность вечерней (и утренней) видимости у Венеры не превышает 4 часов, а у Меркурия – не более 1.5 часа. Можно сказать, что Меркурий всегда «купается» в солнечных лучах – его приходится наблюдать или непосредственно перед восходом Солнца, или сразу после захода, на светлом небе. Видимый блеск (звездная величина) Меркурия меняется со временем в пределах от 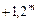 до
до 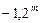 . Видимая звездная величина Венеры варьируется от
. Видимая звездная величина Венеры варьируется от 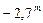 до
до 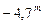 . Венера – самый яркий объект на небе после Солнца и Луны.
. Венера – самый яркий объект на небе после Солнца и Луны.
У внешних планет также различают четыре конфигурации (рис. 7.4): соединение (с.), противостояние (п.), восточная и западная квадратуры (з.кв. и в.кв.).
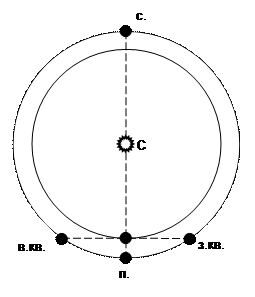
Рис. 7.4. Конфигурации внешних планет
В конфигурации «соединение» внешняя планета расположена на прямой, соединяющей Солнце и Землю, за Солнцем. В этот момент наблюдать ее нельзя.
Так как угловая скорость внешней планеты меньше, чем у Земли, дальнейшее относительное движение планеты на небесной сфере будет попятным. При этом она постепенно будет смещаться к западу от Солнца. Когда угловое удаление внешней планеты от Солнца достигнет 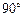 , она попадет в конфигурацию «западная квадратура». При этом планета будет видна в восточной стороне неба всю вторую половину ночи до восхода.
, она попадет в конфигурацию «западная квадратура». При этом планета будет видна в восточной стороне неба всю вторую половину ночи до восхода.
В конфигурации «противостояние», называемой иногда также «оппозиция», планета отстоит на небе от Солнца на 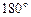 , тогда
, тогда
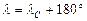 , ,
| (7.13) |
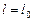 . .
| (7.14) |
После противостояния внешняя планета постепенно приближается к Солнцу, находясь на небе восточнее, то есть, левее нашего дневного светила. В этот период планету можно наблюдать вечером после захода Солнца. Когда угловое удаление Солнца достигнет 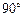 , наступит конфигурация «восточная квадратура», при этом геоцентрическая эклиптическая долгота планеты
, наступит конфигурация «восточная квадратура», при этом геоцентрическая эклиптическая долгота планеты
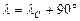 . .
| (7.15) |
Планету, находящуюся в восточной квадратуре, можно наблюдать с вечера до полуночи.
Наиболее благоприятны условия для наблюдений внешних планет в эпоху их противостояния. В это время планета доступна наблюдениям в течение всей ночи. При этом она максимально сближена с Землей и имеет наибольший угловой диаметр и максимальный блеск. Для наблюдателей немаловажно, что все верхние планеты достигают наибольшей высоты над горизонтом в зимние противостояния, когда они движутся по небу в тех же созвездиях, где Солнце бывает летом. Летние же противостояния на северных широтах происходят низко над горизонтом, что может весьма затруднить наблюдения.
При расчете даты той или иной конфигурации планеты ее расположение относительно Солнца изображается на чертеже, плоскость которого принимается за плоскость эклиптики. Направление на точку весеннего равноденствия ^ выбирается произвольно. Если задан день года, в который гелиоцентрическая эклиптическая долгота Земли 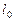 имеет определенное значение, то сначала следует отметить на чертеже расположение Земли.
имеет определенное значение, то сначала следует отметить на чертеже расположение Земли.
Приближенное значение гелиоцентрической эклиптической долготы Земли очень легко найти по дате наблюдения. Легко видеть (рис. 7.5), что, например, 21 марта, смотря с Земли в сторону Солнца, мы смотрим в точку весеннего равноденствия ^, то есть, направление «Солнце – точка весеннего равноденствия» отличается от направления «Солнце – Земля» на 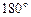 , а это значит, что гелиоцентрическая эклиптическая долгота Земли
, а это значит, что гелиоцентрическая эклиптическая долгота Земли 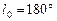 . Смотря на Солнце в день осеннего равноденствия (23 сентября), мы видим его в направлении на точку осеннего равноденствия (на чертеже она диаметрально противоположна точке ^). При этом эклиптическая долгота Земли
. Смотря на Солнце в день осеннего равноденствия (23 сентября), мы видим его в направлении на точку осеннего равноденствия (на чертеже она диаметрально противоположна точке ^). При этом эклиптическая долгота Земли 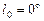 . Из рис. 7.5 видно, что в день зимнего солнцестояния (22 декабря) эклиптическая долгота Земли
. Из рис. 7.5 видно, что в день зимнего солнцестояния (22 декабря) эклиптическая долгота Земли 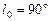 , а в день летнего солнцестояния (22 июня) –
, а в день летнего солнцестояния (22 июня) – 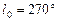 .
.
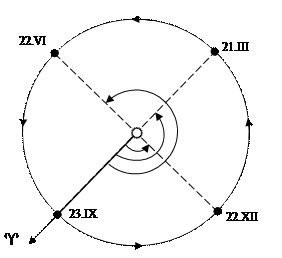
Рис. 7.5. Эклиптические гелиоцентрические долготы Земли
в разные дни года
Для расчета долготы Земли 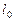 в произвольный день года достаточно вспомнить, что полный оборот в
в произвольный день года достаточно вспомнить, что полный оборот в 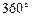 вокруг Солнца Земля совершает за 365 дней. Это значит, что за сутки Земля смещается по своей орбите примерно на
вокруг Солнца Земля совершает за 365 дней. Это значит, что за сутки Земля смещается по своей орбите примерно на 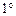 . Например, 1 апреля эклиптическая гелиоцентрическая долгота Земли будет
. Например, 1 апреля эклиптическая гелиоцентрическая долгота Земли будет 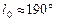 , так как эта дата наступает через 10 дней после дня весеннего равноденствия, когда
, так как эта дата наступает через 10 дней после дня весеннего равноденствия, когда 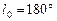 .
.
Гелиоцентрическая эклиптическая долгота Земли 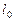 в определенные дни года может быть также найдена по геоцентрической эклиптической долготе Солнца
в определенные дни года может быть также найдена по геоцентрической эклиптической долготе Солнца 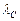 в эти же дни, так как если построить подобную систему эклиптических координат с началом в центре Земли, то всегда
в эти же дни, так как если построить подобную систему эклиптических координат с началом в центре Земли, то всегда 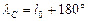 , поскольку Солнце и Земля всегда находятся на противоположных концах одного радиуса-вектора. Но геоцентрическая долгота
, поскольку Солнце и Земля всегда находятся на противоположных концах одного радиуса-вектора. Но геоцентрическая долгота 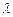 планеты не связана подобной зависимостью со своей гелиоцентрической долготой
планеты не связана подобной зависимостью со своей гелиоцентрической долготой 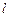 .
.
Затем надо изобразить на чертеже орбиту планеты. Как уже отмечалось, ее можно считать круговой и изображать с помощью циркуля. Крайне важно соблюсти пропорции между радиусами орбит Земли и планеты, в противном случае измерения углов транспортиром окажутся неверными. Напомним, что радиус орбиты Меркурия примерно 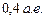 , Венеры –
, Венеры – 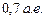 , Марса –
, Марса – 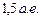 , Юпитера –
, Юпитера – 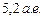
Теперь можно наносить на этот чертеж расположение планеты либо по ее известной гелиоцентрической эклиптической долготе 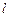 , либо по заданной конфигурации.
, либо по заданной конфигурации.
Построив на чертеже положения планет относительно Солнца, можно измерить транспортиром их геоцентрические долготы 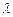 и по разности
и по разности
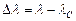 , ,
| (7.16) |
определить условия их видимости с Земли, полагая, что в среднем планета становится видимой при удалении от Солнца на угол около 15º.
В действительности же условия видимости планет зависят не только от их удаления от Солнца, но также и от их склонения 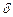 и от географической широты
и от географической широты 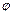 места наблюдения, которая влияет на продолжительность сумерек и на высоту планет над горизонтом.
места наблюдения, которая влияет на продолжительность сумерек и на высоту планет над горизонтом.
Так как положение Солнца на эклиптике хорошо известно для каждого дня года, то по звездной карте и по значениям 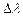 легко указать созвездие, в котором находится планета в тот же день года. Решение этой задачи облегчается тем, что на нижнем обрезе карт Малого звездного атласа А.А. Михайлова красными числами проставлены даты, в которые отмеченные ими круги склонения кульминируют в среднюю полночь. Эти же даты показывают приблизительное положение Земли на своей орбите по наблюдениям с Солнца. Поэтому, определив по карте экваториальные координаты
легко указать созвездие, в котором находится планета в тот же день года. Решение этой задачи облегчается тем, что на нижнем обрезе карт Малого звездного атласа А.А. Михайлова красными числами проставлены даты, в которые отмеченные ими круги склонения кульминируют в среднюю полночь. Эти же даты показывают приблизительное положение Земли на своей орбите по наблюдениям с Солнца. Поэтому, определив по карте экваториальные координаты 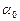 и
и 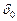 точки эклиптики, кульминирующей в среднюю полночь заданной даты, легко найти для этой же даты экваториальные координаты Солнца
точки эклиптики, кульминирующей в среднюю полночь заданной даты, легко найти для этой же даты экваториальные координаты Солнца
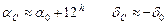
| (7.17) |
и по ним показать его положение на эклиптике.
По гелиоцентрической долготе планет легко вычислить дни (даты) наступления их различных конфигураций. Для этого достаточно перейти к системе отсчета, связанной с планетой. Это предполагает, что в конечном итоге мы планету будем считать неподвижной, а Землю – движущейся по своей орбите, но с относительной угловой скоростью.
Получим необходимые формулы для изучения движения верхней планеты. Пусть в некоторый день года 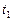 гелиоцентрическая долгота верхней планеты есть
гелиоцентрическая долгота верхней планеты есть 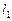 , а гелиоцентрическая долгота Земли –
, а гелиоцентрическая долгота Земли – 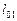 . Верхняя планета движется медленнее Земли (
. Верхняя планета движется медленнее Земли ( 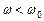 ), которая догоняет планету, и в какой-то день года
), которая догоняет планету, и в какой-то день года 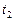 при гелиоцентрической долготе планеты
при гелиоцентрической долготе планеты 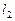 и Земли
и Земли 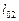 наступит искомая конфигурация планеты. Тогда
наступит искомая конфигурация планеты. Тогда
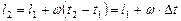 , ,
| (7.18) | |
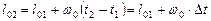 , ,
| (7.19) | |
откуда, обозначив 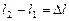 ,
, 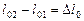 и
и 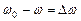 , получим
, получим
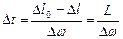
| (7.20) |
и найдем
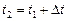 . .
| (7.21) |
Легко видно, что 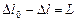 представляет собой угловой путь Земли по орбите, проходимый Землей с относительной угловой скоростью
представляет собой угловой путь Земли по орбите, проходимый Землей с относительной угловой скоростью 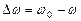 за промежуток времени
за промежуток времени 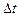 . Поэтому для вычисления
. Поэтому для вычисления 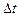 можно полагать планету неподвижной и, взяв разность
можно полагать планету неподвижной и, взяв разность 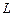 между разностями гелиоцентрической долготы Земли и планеты в моменты времени
между разностями гелиоцентрической долготы Земли и планеты в моменты времени 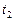 и
и 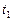 (или найдя
(или найдя 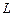 по чертежу), сразу определить
по чертежу), сразу определить 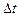 . Для вычисления же гелиоцентрической долготы планеты
. Для вычисления же гелиоцентрической долготы планеты 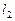 и Земли
и Земли 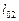 на дату
на дату 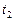 используются формулы (7.18) и (7.19).
используются формулы (7.18) и (7.19).
Очевидно, те же формулы (7.18) – (7.21) служат для вычисления дней наступления конфигураций нижних планет с той лишь разницей, что из-за большой скорости движения нижней планеты по сравнению со скоростью движения Земли в формулы следует подставлять 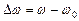 и дугу
и дугу 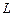 , которую проходит нижняя планета от одной конфигурации до другой при условии неподвижной Земли.
, которую проходит нижняя планета от одной конфигурации до другой при условии неподвижной Земли.
Все рассмотренные выше задачи следует решать приближенно, округляя значения 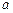 до 0,01 астрономической единицы,
до 0,01 астрономической единицы, 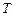 и
и 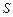 – до 0,01 года и
– до 0,01 года и 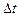 – до целых суток.
– до целых суток.
Дата добавления: 2015-09-29; просмотров: 9650;
