ПИТАНИЯ ОТ НАГРУЗКИ
ИЗУЧЕНИЕ ЗАВИСИМОСТЕЙ ПОЛЕЗНОЙ
МОЩНОСТИ И К.П.Д ИСТОЧНИКА
ПИТАНИЯ ОТ НАГРУЗКИ
1. 1.ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА И ПЛОТНОСТЬ ТОКА
Электрическим током называется всякое упорядоченное движение электрических зарядов. Электрический ток, который возникает как упорядоченное движение свободных зарядов под действием электрического поля в проводящих средах, называется током проводимости.
Кроме тока проводимости существуют другие виды тока. Если какое-то тело зарядить и перемещать в пространстве, то в этом случае электрические заряды будут перемещаться вместе с макроскопическим телом. Такой ток называют конвекционным или переносным.
В случае тока в вакууме микроскопические электрические заряды движутся в пустоте независимо от макроскопических тел (например, потоки электронов в электрической лампе).
Для существования и появления тока необходимы следующие условия:
1) наличие в данной среде свободных носителей заряда, т.е. частиц, которые могли бы упорядоченно перемещаться.
2) существование в данной среде внешнего электрического поля, энергия которого расходуется на упорядоченное перемещение электрических зарядов.
3) источник энергии, пополняющий запас энергии электрического поля.
За положительное направление тока принято направление упорядоченного движения положительных электрических зарядов.
Сила тока – это скалярная величина, равная отношению заряда dq, переносимого через рассматриваемую поверхность dS за малый промежуток времени, к величине dt этого промежутка:
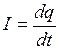 .
.
Если сила и направление тока не меняется во времени, ток называется постоянным:
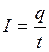 ,
,
где q –заряд, переносимый через рассматриваемую поверхность за конечный интервал времени t.
Сила тока в системе СИ измеряется в Амперах 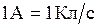 .
.
Характеристикой тока, отражающей его распределение по поверхности, является плотность тока 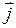 . Плотность тока – векторная величина, направленная противоположно движению электронов, и численно равная отношению силы тока
. Плотность тока – векторная величина, направленная противоположно движению электронов, и численно равная отношению силы тока 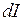 через очень малый элемент поверхности, нормальный к направлению движения зарядов, к величине
через очень малый элемент поверхности, нормальный к направлению движения зарядов, к величине 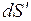 площади этого элемента:
площади этого элемента:
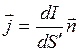 ,
,
где 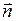 – орт вектора
– орт вектора 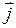 , совпадающий с нормалью к поверхности
, совпадающий с нормалью к поверхности 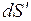 . Для произвольно ориентированного элемента dS имеем:
. Для произвольно ориентированного элемента dS имеем:
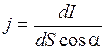 ,
,
где 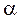 – угол между направлением тока и нормалью к dS.
– угол между направлением тока и нормалью к dS.
Для постоянного тока 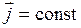 по всему поперечному сечению S однородного проводника, сила тока I = jS.
по всему поперечному сечению S однородного проводника, сила тока I = jS.
Зная вектор 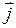 в каждой точке пространства, можно найти силу тока через любую поверхность
в каждой точке пространства, можно найти силу тока через любую поверхность 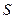 :
:
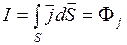 .
.
Таким образом, сила тока есть поток вектора плотности тока 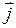 через поверхность S.
через поверхность S.
Электрический ток может быть обусловлен движением как положительных, так и отрицательных носителей. Перенос отрицательного заряда в одном направлении эквивалентен переносу такого же по величине положительного заряда в противоположном направлении.
Если ток создается носителями обоих знаков, и за время dt через данную поверхность положительные носители переносят заряд 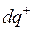 в одном направлении, а отрицательные – заряд
в одном направлении, а отрицательные – заряд 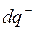 в противоположном, то
в противоположном, то
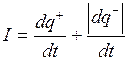 .
.
Поле вектора плотности тока можно изобразить с помощью линий тока, которые стоятся так же, как линии вектора 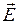 . Линии тока – это кривые, касательные в каждой точке к которым совпадают по направлению с вектором
. Линии тока – это кривые, касательные в каждой точке к которым совпадают по направлению с вектором 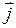 .
.
Пусть в единице объема содержится 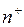 положительных носителей и
положительных носителей и 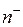 – отрицательных. Алгебраическая величина зарядов носителей равна соответственно
– отрицательных. Алгебраическая величина зарядов носителей равна соответственно 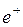 и
и 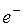 . Если под действием поля носители приобретают средние скорости
. Если под действием поля носители приобретают средние скорости 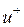 и
и 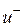 , то за единицу времени через единичную площадку пройдет
, то за единицу времени через единичную площадку пройдет 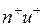 положительных носителей, которые перенесут заряд
положительных носителей, которые перенесут заряд 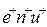 , отрицательные носители перенесут в противоположном направлении заряд
, отрицательные носители перенесут в противоположном направлении заряд 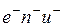 .
.
Тогда плотность тока равна 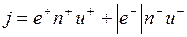 , или в векторной форме
, или в векторной форме 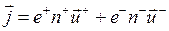 , оба слагаемых имеют одинаковое направление (скорость
, оба слагаемых имеют одинаковое направление (скорость 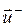 направлена противоположно
направлена противоположно 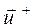 ,
, 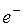 дает знак минус, поэтому
дает знак минус, поэтому 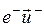 имеет то же направление, что
имеет то же направление, что 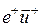 ).
).
Произведение 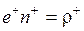 – плотность заряда положительных носителей,
– плотность заряда положительных носителей, 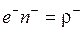 – плотность заряда отрицательных носителей, тогда
– плотность заряда отрицательных носителей, тогда
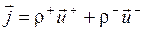 .
.
Рассмотрим некоторую среду, в которой течет ток. Выберем воображаемую замкнутую поверхность S. Заряд, выходящий в единицу времени из объема V,ограниченного поверхностью S, согласно закону сохранения заряда, равен скорости убывания заряда q, содержащегося в данном объеме (рисунок 1)
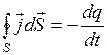 .
.
Но 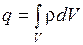 , тогда
, тогда 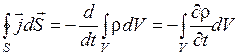 .
.
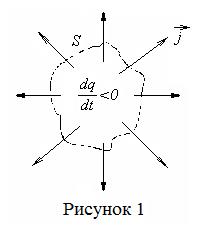 Преобразуем это выражение по теореме Остроградского-Гаусса, имеем
Преобразуем это выражение по теореме Остроградского-Гаусса, имеем 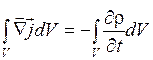 . Это равенство выполняется при произвольном выборе объема V, следовательно, в каждой точке пространства должно выполняться условие
. Это равенство выполняется при произвольном выборе объема V, следовательно, в каждой точке пространства должно выполняться условие
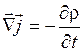 .
.
Это равенство получило название уравнения непрерывности. Оно выражает закон сохранения заряда. Согласно этому уравнению, в точках, которые являются источниками вектора 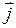 , происходит убывание заряда.
, происходит убывание заряда.
В случае стационарного тока объемная плотность заряда 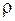 не зависит от времени, тогда уравнение непрерывности имеет вид:
не зависит от времени, тогда уравнение непрерывности имеет вид:
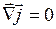
– в случае постоянного тока вектор 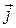 не имеет источников. Это означает, что линии тока нигде не начинаются и нигде не заканчиваются. Следовательно, линии постоянного тока всегда замкнуты, и число линий, входящих в замкнутую поверхность, равно числу линий, выходящих их поверхности,
не имеет источников. Это означает, что линии тока нигде не начинаются и нигде не заканчиваются. Следовательно, линии постоянного тока всегда замкнуты, и число линий, входящих в замкнутую поверхность, равно числу линий, выходящих их поверхности, 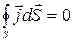 .
.
1.2. ЭЛЕКТРОДВИЖУЩАЯ СИЛА
Циркуляция вектора напряженности электростатического поля равна нулю, поэтому в замкнутой цепи наряду с участками, на которых положительные носители движутся в сторону убывания потенциала  ,
,
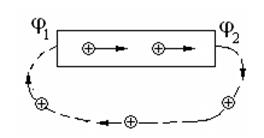 Рисунок 2.
Рисунок 2.
|
должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания 

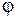 , т. е. против сил электростатического поля. Перемещение носителей на этих участках возможно лишь с помощью сил неэлектрического происхождения, называемых сторонними силами. Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках. Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде и т. д. Сторонние силы действуют на носители тока, вызывая их упорядоченное движение, и поддерживают ток в цепи (рисунок 2).
, т. е. против сил электростатического поля. Перемещение носителей на этих участках возможно лишь с помощью сил неэлектрического происхождения, называемых сторонними силами. Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках. Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде и т. д. Сторонние силы действуют на носители тока, вызывая их упорядоченное движение, и поддерживают ток в цепи (рисунок 2).
Величина, равная работе сторонних сил по перемещению единичного положительного заряда по цепи, называется электродвижущей силой (ЭДС) 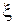 :
:
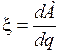 .
.
Если на заряд q действует сторонняя сила 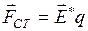 , где
, где 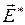 –напряженность поля сторонних сил, то работа сторонних сил над зарядом q на участке цепи 1-2 равна:
–напряженность поля сторонних сил, то работа сторонних сил над зарядом q на участке цепи 1-2 равна:
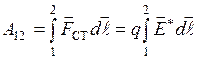 .
.
Для ЭДС на участке цепи имеем:
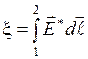 .
.
Если цепь замкнута 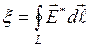 – ЭДС равна циркуляции вектора напряженности поля сторонних сил. Кроме сторонних сил, на заряд действуют силы электростатического поля:
– ЭДС равна циркуляции вектора напряженности поля сторонних сил. Кроме сторонних сил, на заряд действуют силы электростатического поля:
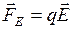 .
.
Результирующая всех сил:
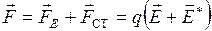 .
.
Работа этой силы под зарядом q на участке 1-2
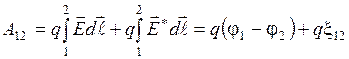
Для единичного положительного заряда
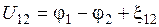
– мы получили выражение для падения напряжения на данном участке.
Падением напряжения 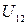 (или просто напряжением) на участке цепи 1-2 называется физическая величина, численно равная работе, совершаемой суммарным полем кулоновских и сторонних сил при перемещении вдоль цепи единичного положительного заряда из точки 1 в точку 2.
(или просто напряжением) на участке цепи 1-2 называется физическая величина, численно равная работе, совершаемой суммарным полем кулоновских и сторонних сил при перемещении вдоль цепи единичного положительного заряда из точки 1 в точку 2.
Если 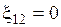 (сторонние силы не действуют) участок называется однородным:
(сторонние силы не действуют) участок называется однородным: 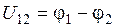 .
.
1.3. ЗАКОН ОМА. СОПРОТИВЛЕНИЕ
Закон Ома был экспериментально открыт в 1826 году в следующей форме:
Сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
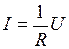 , (1)
, (1)
где R электрическое сопротивление проводника, 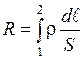 ,
, 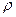 -удельное сопротивление (
-удельное сопротивление ( 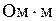 ),
), 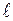 – длина, S – площадь сечения проводника.
– длина, S – площадь сечения проводника.
Однородным называется такой участок цепи, на котором действуют только электростатические силы. Выражение 1) определяет соотношение между током и напряжением для однородного участка цепи и называется законом Ома в интегральной форме.
Единица сопротивления – Ом, 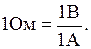
Сопротивление проводника определяется его геометрическими размерами ( 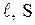 ) и материалом, из которого этот проводник изготовлен. Наименьшими удельными сопротивлениями обладают серебро, медь, золото, алюминий. Величина ϭ, обратная удельному сопротивлению, называется удельной электропроводимостью или электропроводностью вещества. В дифференциальной форме закон Ома принимает вид:
) и материалом, из которого этот проводник изготовлен. Наименьшими удельными сопротивлениями обладают серебро, медь, золото, алюминий. Величина ϭ, обратная удельному сопротивлению, называется удельной электропроводимостью или электропроводностью вещества. В дифференциальной форме закон Ома принимает вид:
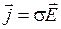
– вектор плотности тока равен произведению электропроводности и вектора напряженности электростатического поля.
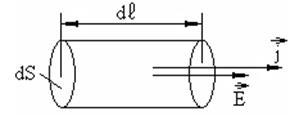 Рисунок 3.
Рисунок 3.
|
Действительно, рассмотрим однородный участок проводника, в пределах которого площадь сечения остается постоянной (рисунок 3). Тогда сила тока равна 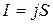 , связь напряженности и потенциала дает значение напряжения
, связь напряженности и потенциала дает значение напряжения 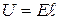 , сопротивление участка определяется формулой
, сопротивление участка определяется формулой 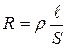 . Подставив в формулу (1), имеем:
. Подставив в формулу (1), имеем: 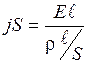 ; отсюда
; отсюда 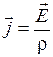 или
или 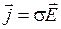 .
.
Закон Ома объясняет классическая теория металлов, созданная физиками Друде и Лоренцем. Согласно этой теории валентные электроны в металле являются общими для всех атомов и движутся в пространстве между положительными ионами, которые находятся в узлах кристаллических решеток. Электроны проводимости образуют электронный газ, подчиняющийся законам идеального газа. Однако, в отличие от молекул идеального газа, которые при движении сталкиваются друг с другом, электроны в металле сталкиваются с узлами кристаллической решетки, и расстояние, которое проходит электрон между двумя такими соударениями, есть длина свободного пробега электрона λ. В результате таких столкновений устанавливается тепловое равновесие между электронным газом и кристаллической решеткой. Друде распространил на электронный газ результаты кинетической теории газов. В этой теории средняя скорость теплового движения электронов равна 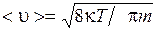 , при комнатной температуре
, при комнатной температуре 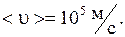 При внесении проводника в поле, на хаотическое тепловое движение электронов накладывается упорядоченное движение электронов с некоторой средней скоростью
При внесении проводника в поле, на хаотическое тепловое движение электронов накладывается упорядоченное движение электронов с некоторой средней скоростью 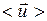 , при этом плотность тока:
, при этом плотность тока:
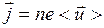 .
.
Максимально возможное значение 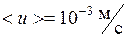 , т.е. в
, т.е. в 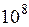 раз меньше средней скорости теплового движения
раз меньше средней скорости теплового движения 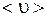 .
.
Найдем изменение кинетической энергии электронов, вызываемое полем. Для этого определим средний квадрат результирующей скорости:
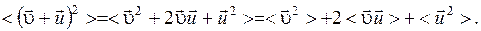
Величины 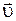 и
и 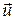 независимы, поэтому
независимы, поэтому 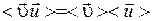 ,
, 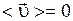 (среднее значение вектора скорости теплового движении электронов равно нулю, т.к. ее направление меняется хаотично), следовательно,
(среднее значение вектора скорости теплового движении электронов равно нулю, т.к. ее направление меняется хаотично), следовательно,
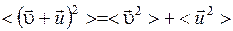 .
.
Таким образом, упорядоченное движение увеличивает кинетическую энергию электронов на
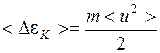 .
.
Двигаясь в кристалле, электроны испытывают соударение с узлами кристаллической решетки. Время между двумя соударениями:
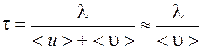 ,
,
где 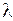 – длина свободного пробега электрона в металле.
– длина свободного пробега электрона в металле.
Друде предположил, что при соударении электронов с узлом кристаллической решетки вся дополнительная энергия передается иону, в результате соударения u = 0. Если поле, ускоряющее электроны, однородно, электрон получает постоянное ускорение 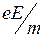 , и к концу пробега скорость упорядоченного движения достигает максимума (рисунок 4)
, и к концу пробега скорость упорядоченного движения достигает максимума (рисунок 4)
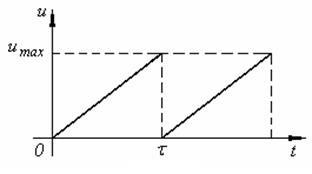 Рисунок 4. Рисунок 4.
|
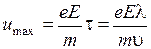 .
.
Скорость u изменяется во времени линейно, поэтому
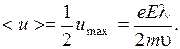
Для плотности тока j получим: 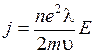 , т. е., j ~ E – это закон Ома. Коэффициент пропорциональности
, т. е., j ~ E – это закон Ома. Коэффициент пропорциональности 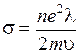 есть проводимость. Если бы электроны не сталкивались с ионами кристаллической решетки, их скорости росли бы беспрепятственно, и проводимость была бы неограниченно большой
есть проводимость. Если бы электроны не сталкивались с ионами кристаллической решетки, их скорости росли бы беспрепятственно, и проводимость была бы неограниченно большой 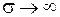 , т.к. неограниченно росла бы при этом длина свободного пробега.
, т.к. неограниченно росла бы при этом длина свободного пробега.
Сопротивление проводника зависит от температуры и давления. Сопротивление металлических проводников зависит от температуры по закону
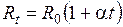 ,
,
где 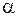 – температурный коэффициент сопротивления. Для некоторых металлов и сплавов вблизи абсолютного нуля температуры наблюдается скачкообразное падение сопротивления практически до нуля. Это явление называют сверхпроводимостью. Температура перехода в сверхпроводящее состояние для разных металлов лежит в интервале от 2 до 10 К.
– температурный коэффициент сопротивления. Для некоторых металлов и сплавов вблизи абсолютного нуля температуры наблюдается скачкообразное падение сопротивления практически до нуля. Это явление называют сверхпроводимостью. Температура перехода в сверхпроводящее состояние для разных металлов лежит в интервале от 2 до 10 К.
1.4. ЗАКОН ОМА ДЛЯ НЕОДНОРОДНОГО УЧАСТКА ЦЕПИ
На носители тока на неоднородном участке цепи действуют, кроме электростатических сил 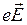 , еще и сторонние силы
, еще и сторонние силы 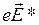 . Сторонние силы способны вызывать упорядоченное движение носителей тока так же, как и силы электростатические. На неоднородном участке цепи средняя скорость упорядоченного движения носителей пропорциональна суммарной силе
. Сторонние силы способны вызывать упорядоченное движение носителей тока так же, как и силы электростатические. На неоднородном участке цепи средняя скорость упорядоченного движения носителей пропорциональна суммарной силе 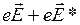 , тогда плотность тока
, тогда плотность тока
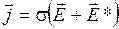 , (2)
, (2)
это закон Ома для неоднородного участка цепи в дифференциальной форме.
Перейдем к интегральной форме этого закона. Рассмотрим неоднородный участок цепи. Допустим, что внутри этого участка существует линия (контур тока) удовлетворяющая следующим условиям:
1) в каждом сечении, перпендикулярном к контуру, величины 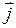 ,
, 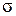 ,
, 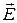 и
и 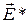 имеют с достаточной точностью одинаковые значения;
имеют с достаточной точностью одинаковые значения;
2) векторы 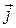 ,
, 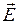 ,
, 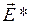 в каждой точке направлены по касательной к контуру. Поперечное сечение проводника может быть непостоянным.
в каждой точке направлены по касательной к контуру. Поперечное сечение проводника может быть непостоянным.
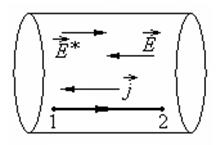 Рисунок 5.
Рисунок 5.
|
Выберем произвольно направление движения по контуру (рисунок 5). Пусть выбранное направление соответствует перемещению от конца 1 к концу 2 участка цепи. Спроектируем выражение (2) на элемент контура1-2:
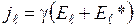 , (3)
, (3)
причем 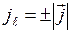 ;
; 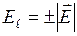 ;
; 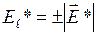 . Знак «+» берем в том случае, если ток течет от 1 к 2, «-»если ток течет в направлении 2 к 1. Вследствие сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой. Поэтому вдоль контура
. Знак «+» берем в том случае, если ток течет от 1 к 2, «-»если ток течет в направлении 2 к 1. Вследствие сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой. Поэтому вдоль контура 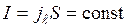 . Силу тока в данном случае нужно рассматривать как алгебраическую величину. Направление 1-2 выбрано произвольно, поэтому, если ток течет в выбранном направлении, его считают положительным, если в направлении 2-1 – отрицательным. Заменим
. Силу тока в данном случае нужно рассматривать как алгебраическую величину. Направление 1-2 выбрано произвольно, поэтому, если ток течет в выбранном направлении, его считают положительным, если в направлении 2-1 – отрицательным. Заменим 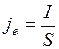 ;
; 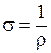 , тогда из (3):
, тогда из (3):
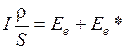 .
.
Умножим это выражение на 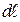 и проинтегрируем вдоль контура:
и проинтегрируем вдоль контура:
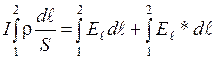 .
.
Здесь 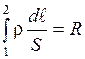 – сопротивление всей цепи,
– сопротивление всей цепи, 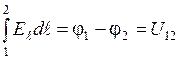 – разность потенциалов на сопротивление R,
– разность потенциалов на сопротивление R, 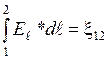 – ЭДС, действующая на участки 1,2. Тогда
– ЭДС, действующая на участки 1,2. Тогда 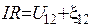 , а ток
, а ток
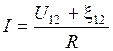
– это закон Ома для неоднородного участка цепи.
Если цепь замкнутая, то 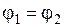 ; и
; и 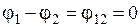 .Тогда
.Тогда 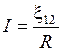 – закон Ома для замкнутой цепи. Если в цепи действует несколько ЭДС, то
– закон Ома для замкнутой цепи. Если в цепи действует несколько ЭДС, то 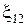 равна их алгебраической сумме.
равна их алгебраической сумме.
1.5. МОЩНОСТЬ ТОКА
Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через каждое сечение проводника проходит заряд q = It,что равносильно переносу заряда q из одного конца проводника на другой. При этом силы электростатического поля и сторонние силы совершают работу 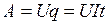 , тогда мощность
, тогда мощность
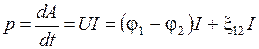 .
.
Эта мощность может расходоваться на совершение работы участком цепи над внешними телами (для этого участок должен перемещаться в пространстве), на протекание химической реакции и на перемещение данного участка цепи.
Отношения мощности dp, развиваемой в объеме dV, к величине этого объема, называется удельной мощностью тока
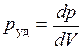 .
.
Найдем выражение для удельной мощности тока. Сила 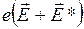 развивает при движении носителя тока мощность:
развивает при движении носителя тока мощность:
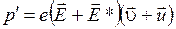 ,
,
где 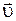 – скорость хаотического движения,
– скорость хаотического движения, 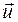 – скорость упорядоченного движения носителей.
– скорость упорядоченного движения носителей.
Усредним это выражение по носителям, заключенным в объеме dV, в пределах которого 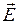 и
и 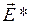 можно считать постоянными:
можно считать постоянными:
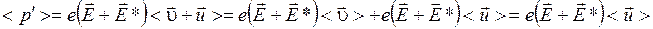 .
.
Мощность 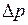 , развиваемую в объеме
, развиваемую в объеме 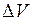 , найдем, умножив
, найдем, умножив 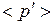 на число носителей тока в этом объеме.
на число носителей тока в этом объеме.
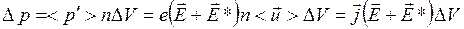 .
.
Подставив 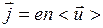 , имеем:
, имеем:
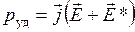
1.6. ЗАКОН ДЖОУЛЯ – ЛЕНЦА
Если ток в цепи постоянен, а проводники, входящие в цепь, неподвижны, работа сторонних сил полностью расходуется на нагревание проводников. Тепловую энергию обозначим W.
Объемной плотностью тепловой мощности тока 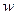 называется энергия, выделяющаяся в единице объема проводника за единицу времени. Закон Джоуля -Ленца в дифференцированной форме имеет вид:
называется энергия, выделяющаяся в единице объема проводника за единицу времени. Закон Джоуля -Ленца в дифференцированной форме имеет вид:
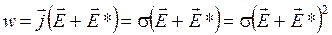
– объемная плотность тепловой мощности тока равна скалярному произведению векторов плотности тока 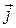 и напряженности электрического поля.
и напряженности электрического поля.
Объемная плотность тепловой мощности тока прямо пропорциональна квадрату напряженности электрического поля, создающего ток, и удельной проводимости проводника.
Интегрируя это выражение по объему проводника, получим закон Джоуля – Ленца в интегральной форме: количество теплоты, выделяемой в проводнике, пропорционально силе тока, времени его прохождения и падению напряжения:
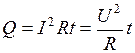 .
.
Классическая электронная теория дает следующее объяснение рассматриваемому выше закону. Кинетическая энергия электрона в конце пробега
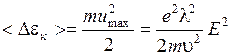 .
.
При столкновении с ионом кристаллической решетки электрон отдает свою энергию, поэтому внутренняя энергия металла возрастает (металл нагревается), число соударений одного электрона 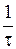 , поэтому в единицу времени в единице объема выделяется тепло:
, поэтому в единицу времени в единице объема выделяется тепло:
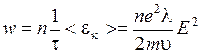 .
.
Для энергии dW имеем: 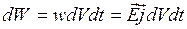 , причем объем
, причем объем 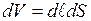 .
.
Проинтегрировав это выражение, получаем: 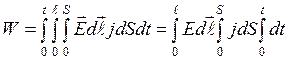 , причем
, причем 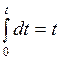 ,
, 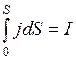 , тогда
, тогда 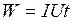 .
.
Таким образом, количество теплоты, выделяемой в проводнике, равно
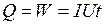 .
.
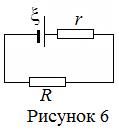 Рассмотрим электрическую цепь, состоящую из источника тока с ЭДС
Рассмотрим электрическую цепь, состоящую из источника тока с ЭДС 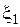 и внутренним сопротивлением r и нагрузки сопротивлением R (рисунок 6).
и внутренним сопротивлением r и нагрузки сопротивлением R (рисунок 6).
По закону Ома ток в цепи равен:
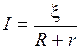 .
.
Напряжения на нагрузке U совпадает с напряжением на зажимах источника и равно:
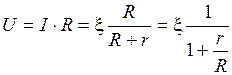 .
.
Напряжение U всегда меньше 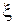 , если цепь разомкнута, R→∞ и U =
, если цепь разомкнута, R→∞ и U = 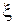 .
.
Полная мощность, развиваемая в цепи источником тока равна
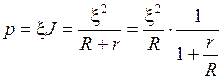 . (4)
. (4)
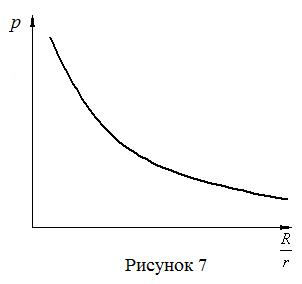
Зависимость полной мощности по отношению 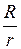 представлена на рисунке 7.
представлена на рисунке 7.
На нагрузке выделяется не вся мощность р, а часть её, называемая полезной:
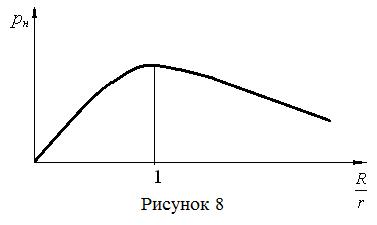
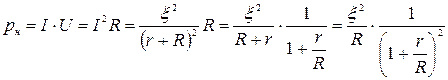 . (5)
. (5)
Полезная мощность имеет максимальные значения, когда производная функции 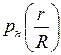 по переменной R равна нулю:
по переменной R равна нулю: 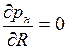 . Это имеет место при R = r.
. Это имеет место при R = r.
Зависимость полезной мощности от отношения 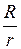 представлена на рисунке 8.
представлена на рисунке 8.
 КПД источника – это отношение полезной мощности к полной:
КПД источника – это отношение полезной мощности к полной: 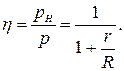 КПД будет тем больше, чем меньше отношение
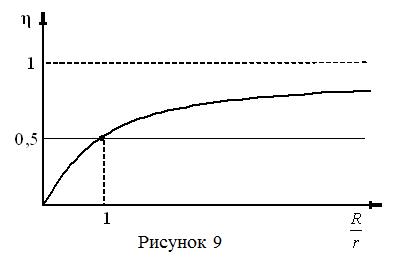
КПД будет тем больше, чем меньше отношение 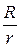 , т.е. чем больше сопротивление нагрузки R (рисунок 9). При размыкании цепи R→∞ и η = 1. Однако при этом мощность, выделяемая во внешней цепи, стремиться к нулю, поэтому условие максимума КПД с практической точки зрения не интересно. Наиболее притягательная область R~r, в которой полезная мощность наибольшая и η~0,5.
, т.е. чем больше сопротивление нагрузки R (рисунок 9). При размыкании цепи R→∞ и η = 1. Однако при этом мощность, выделяемая во внешней цепи, стремиться к нулю, поэтому условие максимума КПД с практической точки зрения не интересно. Наиболее притягательная область R~r, в которой полезная мощность наибольшая и η~0,5.
2.ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ИЗМЕРЕНИЙ
Для исследования мощности используется лабораторная установка (рисунок 10), выполненная ввиде прибора настольного типа и содержащая смонтированные в одном корпусе специализированный источник питания, который по своим характеристикам является аналогом аккумулятора; стрелочный вольтмиллиамперметр с пределами измерений напряжения от 0 до 25В; нагрузка-реостат с сопротивлением несколько сот Ом. Питание установки осуществляется от сети напряжением 220 В. На лицевой панели прибора (рисунок 10) расположены клавиша 1 включения источника питания «ВКЛ», шкала вольтмиллиамперметра, стрелочный прибор измерений I/U. В положении «I» стрелочный прибор показывает силу тока, вположении«U» - напряжение на нагрузке. Потенциометр меняет сопротивление R нагрузки от нуля до максимального значения.
|
|
|
|

| |
|

|


Рис.10
В работе предусматривается определение внутреннего сопротивления r и ЭДС источника двумя способами – графическим и расчетным.
Графический метод определения внутреннего сопротивления и ЭДС источника состоит в следующем. Меняя сопротивление R реостата потенциометром, фиксируют соответствующие значения тока I и напряжения U на нагрузке. По формуле
pН = IU (6)
вычисляют полезную мощность,
а по формуле
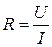 (7)
(7)
сопротивление нагрузки, и строят зависимость pН(R) . По графику определяют сопротивление R, при котором pН достигает максимума. В этом случае R = r.
По закону Ома
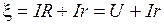 (8)
(8)
– по этой формуле вычисляют ЭДС источника.
Зная R и r, строят зависимости 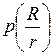 ,
, 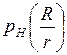 ,
, 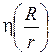 . При этом должно выполняться соотношение h(1) = 0,5.
. При этом должно выполняться соотношение h(1) = 0,5.
Более точный метод определения r и 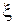 основан на применении метода наименьших квадратов (МНК) и включает в себя обработку результатов эксперимента на ЭВМ (см. Приложение 1). По данным эксперимента строят зависимость
основан на применении метода наименьших квадратов (МНК) и включает в себя обработку результатов эксперимента на ЭВМ (см. Приложение 1). По данным эксперимента строят зависимость 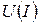 и апроксимируют ее прямой, уравнение которой имеет вид:
и апроксимируют ее прямой, уравнение которой имеет вид:
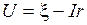 .
.
Напряжение U откладывают по оси ординат, ток I – по оси абсцисс. Точка пересечения этой прямой с осью ординат соответствует значению 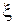 , тангенс угла наклона к оси абсцисс – сопротивлению r.
, тангенс угла наклона к оси абсцисс – сопротивлению r.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Проверив подключение реостата к клеммам установки, включить сетевой шнур в розетку. На лицевой панели включить клавишу 1 «ВКЛ».
2. Перемещая движок реостата и изменяя напряжение от минимума до 20 зафиксировать не менее 10 значений тока 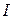 и напряжения
и напряжения 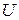 .
.
3. Отключить установку в последовательности, обратной процедуре включения.
4. По результатам измерений рассчитать значения сопротивления нагрузки 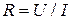 , полезной мощности
, полезной мощности 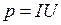 , полной мощности
, полной мощности 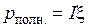 (полагая
(полагая 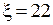 В) и к.п.д.
В) и к.п.д. 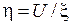 .
.
5. Результаты измерений и вычислений занести в таблицу 1.
Таблица 1
| № п/п | 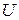 (В) (В)
| 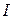 (мА) (мА)
| 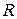 (Ом) (Ом)
| рН(Вт) | р (Вт) | 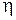
|
| . . |
6. Построить графики зависимостей 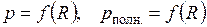 (на одном графике) и
(на одном графике) и 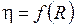 . По максимуму полезной мощности и значению к.п.д.
. По максимуму полезной мощности и значению к.п.д. 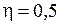 определить величину внутреннего сопротивления источника
определить величину внутреннего сопротивления источника 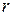 .
.
7. Провести обработку результатов на ЭВМ. Предварительно необходимо ознакомиться с инструкцией по обработке результатов физического практикума на ЭВМ.
4. ОБРАБОТКА РЕЗУЛЬТАТОВ
1. Рассчитать значения сопротивления нагрузки по формуле (7) и полезную мощность по формуле (6). Результаты расчетов свести в таблицу 1.
2. Построить график зависимости 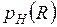 . Определить точку R = r.
. Определить точку R = r.
3. По формуле (8) определить ЭДС 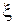 источника.
источника.
4. Произвести оценку полной мощности, развиваемой источником для всех значений тока I по формуле: 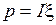 (полагая
(полагая 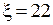 В).
В).
5. Рассчитать КПД источника по формуле 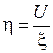 .
.
6. Результаты расчетов п.п. 5,6 свести в таблицу 1.
7. Построить графики зависимостей 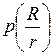 ,
, 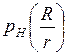 ,
, 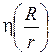 .
.
8. Обработать результаты эксперимента на ЭВМ. Сравнить 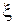 и r с рассчитанными в п.п. 3, 4.
и r с рассчитанными в п.п. 3, 4.
5. ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА НА ЭВМ
Для ввода результатов эксперимента в компьютер необходимо обозначить у = U, х = I, данные представить в виде таблицы 2:
Таблица 2
| х | у | |
| . . . |
Результаты расчетов выдаются на дисплей в виде двух чисел: а = – r; b = 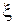 .
.
6. СОДЕРЖАНИЕ ОТЧЕТА
Отчет по работе должен содержать название работы, ее цель, краткие теоретические сведения, рисунок лабораторной установки и электрические схемы опытов, сводку расчетных формул, результаты эксперимента с расчетом погрешностей, таблицы обработки результатов 1 и 2, выводы по работе.
7. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое напряжение? Какова связь понятий напряжения, ЭДС, разность потенциалов?
2. Сформулируйте закон Ома для неоднородного участка цепи. Запишите его дифференциальную и интегральную форму?
3. Что такое полная мощность цепи? Почему не вся полная мощность идет на нагрузку?
4. Как зависит коэффициент полезного действия от отношения 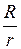 ?
?
5. При каких условиях полезная мощность максимальна?
6. Как экспериментально определить внутреннее сопротивление источника?
7. Как экспериментально определить ЭДС?
8. Проанализируйте графики зависимостей 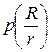 ,
, 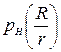 ,
, 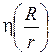 .
.
9. Правильно ли следующее утверждение: «Если сопротивление нагрузки равно внутреннему сопротивлению источника, то полезная мощность максимальна. Сопротивление нагрузки – несколько сот Ом. Следовательно, внутреннее сопротивление r надо выбирать как можно ближе к R»?
8. СПИСОК ЛИТЕРАТУРЫ
1. Иродов И. Е. Электромагнетизм.  : Учебное пособие /И. Е. Иродов. – М: Физматлит.2001- 430с.
: Учебное пособие /И. Е. Иродов. – М: Физматлит.2001- 430с.
2. Савельев И. В. Курс общей физики .В 3-х т. [Текст] : Учебное пособие / И. В. Савельев. – Изд.5-е,стереотип. – СПб.: Изд-во “Лань”, 2006. - Т.2. Электричество и магнетизм. Оптика. – 496с.
ПРИЛОЖЕНИЕ 1
Дата добавления: 2015-09-07; просмотров: 610;
