ПРИМЕНЕНИЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ

ДЛЯ ОПТИМИЗАЦИИ ЛИНЕЙНОЙ ЗАВИСИМОСТИ

Рассмотрим эксперимент, в котором исследуется зависимость одной физической величины ( 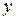) от другой ( 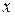). Известно, что эта зависимость должна быть линейной

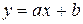(п.1)

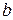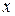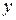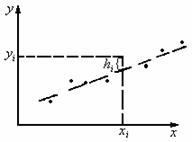
и задача состоит в определении коэффициентов а и . Проводится серия измерений величины и соответствующих значений , что дает набор экспериментальных точек 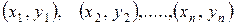. За счет погрешностей измерений эти точки, вообще говоря, не лежат на одной прямой. Требуется подобрать оптимальную прямую, к которой наиболее близки все экспериментальные точки, то есть сумма квадратов вертикальных отклонений точек от искомой прямой должна быть минимальна. Следовательно, требуется найти значения коэффициентов а и 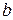, при которых достигается минимум выражения

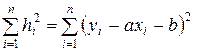. (п.2)

Условия минимума – равенство нулю частных производных по а и 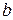от выражения (п.2) – дают систему уравнений

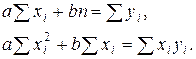(п.3)

Решая ее, находим значения коэффициентов

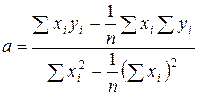, (п.4)

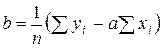. (п.5)

Для того чтобы убедиться, что связь между переменными удовлетворительно описывается линейной зависимостью, вычисляют коэффициент корреляции

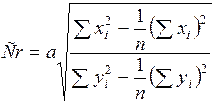. (п.6)

Он подчиняется условию: 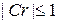. Чем ближе 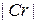к единице, тем теснее точки группируются около прямой линии. Среднеквадратичные погрешности в определении коэффициентов вычисляются по формулам

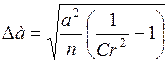, (п.7)

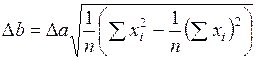. (п.8)

Все эти вычисления можно провести на ЭВМ по имеющейся программе. При этом, чтобы записать формулу вида (8) в виде (п.1), нужно обозначить

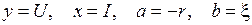. (п.9)