НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЖИДКОСТИ В ТРУБАХ
Неустановившееся движение - движение, когда скорость и давление в отдельных точках потока жидкости изменяются по времени. В этом случае скорость и давление являются функцией не только положения ее отдельной точки относительно выбранных координат, но и времени. Следовательно, средняя скорость в живом сечении потока и расход его изменяются по времени.
В практике эксплуатации систем водоснабжения и водоотведения достаточно часто встречаются случаи неустановившегося движения потоков. Неустановившееся движение наблюдается как в напорных трубах, так и в открытых руслах.
В напорных трубах поток жидкости ограничен жесткими стенками. Площадь живого сечения потока не зависит от времени и может являться функцией расстояния вдоль трубы, т.е. 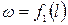 . На расход Q расстояние
. На расход Q расстояние 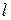 не влияет. Расход жидкости зависит от времени, т.е.
не влияет. Расход жидкости зависит от времени, т.е. 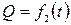 . Однако скорость связана с площадью сечения, следовательно,
. Однако скорость связана с площадью сечения, следовательно, 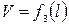 .
.
Средняя скорость потока для данного момента времени
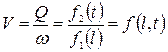 .
.
Для получения уравнения, описывающего изменения гидродинамических характеристик потоков при неустановившемся движении, используется уравнение неустановившегося движения для элементарной струйки несжимаемой жидкости.
Уравнение неустановившегося движения для элементарной струйки вязкой несжимаемой жидкости записывается в виде уравнения Бернулли для двух живых сечений 1-1 и 2-2:
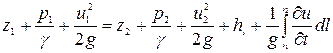 , (5.45)
, (5.45)
где 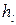 - потери напора по длине струйки между сечениями.
- потери напора по длине струйки между сечениями.
Интеграл 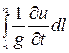 по аналогии с другими слагаемыми уравнения Бернулли называют инерционным напором
по аналогии с другими слагаемыми уравнения Бернулли называют инерционным напором 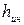 .
.
В зависимости от вида ускорения движения инерционный напор может быть как положительным, так и отрицательным. Для ускоренного движения потока интеграл положительный, а для замедленного движения - отрицательный.
При неустановившемся движении жидкости в трубах на определенном участке длиной 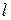 также учитывается инерционный напор
также учитывается инерционный напор 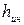 .
.
В цилиндрической трубе площадь сечения 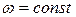 по длине потока, средние скорости
по длине потока, средние скорости 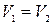 и
и 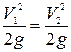 для рассматриваемого момента времени.
для рассматриваемого момента времени.
Потери напора по длине на участке от сечения 1-1 до сечения 2-2 определяются по формуле Дарси-Вейсбаха:
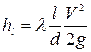 .
.
Ускорение 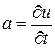 постоянно по длине участка трубы; следовательно, инерционный напор
постоянно по длине участка трубы; следовательно, инерционный напор
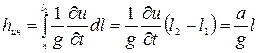 . (5.46)
. (5.46)
Уравнение неустановившегося движения в трубе согласно (5.45)
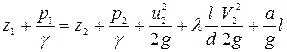 . (5.47)
. (5.47)
Данное уравнение (5.47) - основное уравнение неустановившегося движения жидкости для цилиндрической трубы.
Подобно потерям напора, инерционный напор 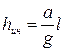 влияет на значение полной удельной энергии во втором сечении. Величина и знак инерционного напора зависят от значения и направления ускорения потока. При замедляющемся движении (
влияет на значение полной удельной энергии во втором сечении. Величина и знак инерционного напора зависят от значения и направления ускорения потока. При замедляющемся движении ( 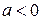 ) инерционный напор будет отрицательным, т.е. на пути между расчетными сечениями будет высвобождаться кинетическая энергия; и если потери напора по длине на этом участке будут невелики (
) инерционный напор будет отрицательным, т.е. на пути между расчетными сечениями будет высвобождаться кинетическая энергия; и если потери напора по длине на этом участке будут невелики ( 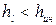 ), то полный напор для данного момента времени между расчетными сечениями будет возрастать. При положительном ускорении потока (
), то полный напор для данного момента времени между расчетными сечениями будет возрастать. При положительном ускорении потока ( 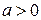 ) за тот же промежуток времени между сечениями удельная энергия жидкости уменьшается.
) за тот же промежуток времени между сечениями удельная энергия жидкости уменьшается.
Дата добавления: 2015-09-29; просмотров: 813;
