Краткая теория. Изучение рассеяния рентгеновских лучей с энергией 20–50 кэВ явилось важным этапом в становлении квантовой теории вещества
Изучение рассеяния рентгеновских лучей с энергией 20–50 кэВ явилось важным этапом в становлении квантовой теории вещества. Обнаружение Комптоном изменения длины волны рентгеновского излучения при его рассеянии веществом, содержащим легкие атомы, подтвердило универсальный характер соотношения 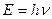 . До опытов Комптона полагалось, что данное соотношение применимо только для оптической области частот. Теперь же мы получили прямые доказательства того, что фотонную структуру имеет и более высокочастотное электромагнитное излучение. Кроме того, эксперименты Комптона дают дополнительные доказательства справедливости специальной теории относительности.
. До опытов Комптона полагалось, что данное соотношение применимо только для оптической области частот. Теперь же мы получили прямые доказательства того, что фотонную структуру имеет и более высокочастотное электромагнитное излучение. Кроме того, эксперименты Комптона дают дополнительные доказательства справедливости специальной теории относительности.
С классической точки зрения рентгеновское излучение представляет собой электромагнитные волны, которые при взаимодействии с атомами вещества способны вызвать вынужденные колебания электронов. При этом естественно ожидать, что частота рассеянного излучения должна совпадать с частотой падающего излучения. Однако, экспериментально было обнаружено, что при рассеянии рентгеновских и гамма–лучей длина волны в спектре рассеянного излучения кроме первоначальной длины волны возбуждающего излучения появляется более длинные волны. Анализ этого явления, названного в последствии эффектом Комптона, позволило А.Комптону установить следующее:
· в рассеянном излучении присутствуют как первоначальная длина волны возбуждающего излучения, так и длина волны, смещенная в сторону более длинных волн;
· величина смещения зависит от угла рассеяния и возрастает при его увеличении;
· при увеличении угла рассеяния интенсивность несмещенной линии падает, а интенсивность смещенной линии возрастает;
· особенности этого явления объясняются, предположив, что рентгеновское излучение имеет чисто корпускулярную природу.
Рассмотрим более подробно явление рассеяние жестких рентгеновских лучей в графите, выполненные А.Комптоном в 1922 г. Схема опыта показана на рис.1. В опыте Комптона рентгеновские лучи, возникающие в трубке с молибденовым антикатодом при разности потенциалов 50 кВ, рассеивались в графитовой мишени. Длина волны падающего излучения отвечала так называемой Мо К–линии с длиной волны 0,7  =0,7×10-8 см, что соответствует энергии около 20 кэВ. Эта энергия весьма высока по сравнению с энергией связи почти всех электронов атома углерода.
=0,7×10-8 см, что соответствует энергии около 20 кэВ. Эта энергия весьма высока по сравнению с энергией связи почти всех электронов атома углерода.
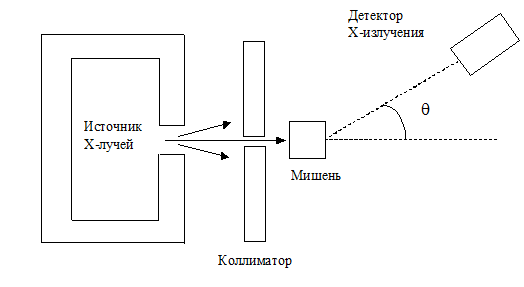
Рис. 1 - Схема эксперимента Комптона
Экспериментальные спектры рассеяния при разных углах рассеяния q представлены на рис.2.

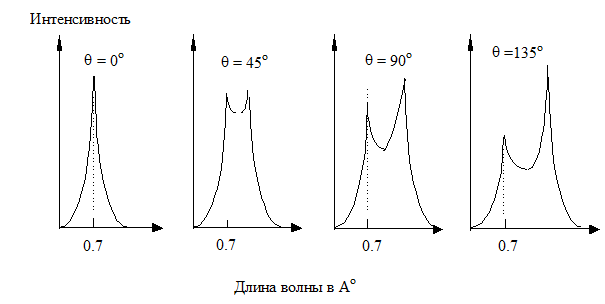
Рис. 2 - Экспериментальные спектры рассеяния
В спектре рассеянного излучения присутствует две линии: одна линия идентична по своим свойствам рассеиваемому излучению, а вторая линия имеет длину волны, которая зависит от угла рассеяния и сдвинута относительно длины волны падающего излучения в длинноволновую область.
Происхождение первой линии легко понять, исходя из волновых представлений падающего излучения. Первичное излучение заставляет электроны атомов вещества колебаться со своей собственной частотой n, и осциллирующие электроны являются источником излучения той же частоты n. В этом процессе происходит лишь временное изменение состояния атома, и электроны не испускаются. Можно ожидать, что такого рода рассеяние будут испытывать главным образом сильно связанные электроны атома, располагающихся на внутренних электронных оболочках (рис.3).
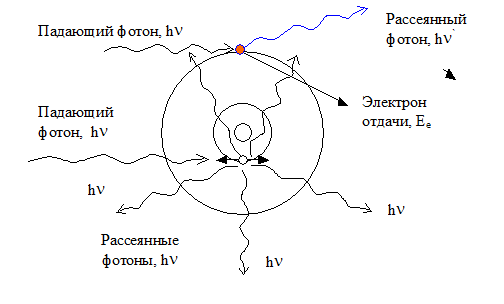
Рис. 3 - Рассеяние первичного излучения сильносвязанными электронами внутренних оболочек и слабосвязанными электронами внешних электронных оболочек атома
Электроны, располагающиеся на внешних электронных оболочках имеют малые энергии связи (10 – 100 эВ) по сравнению с энергией рентгеновского излучения. В таких условиях можно ожидать, что процесс рассеяния рентгеновского излучения будет происходить как на свободных электронах и они могут быть выброшены из атома в процессе рассеяния. В опытах Комптона удалось зарегистрировать электроны отдачи и показать, что электрон отдачи и рассеянное излучение коррелированы друг с другом. Поэтому именно рассеяние на внешних электронах отвечает за появление новой длинноволновой компоненты.
Для количественного анализа рассеяния А. Комптон применил квантовую теорию, согласно которой электромагнитное излучение представляется как состоящее из потока фотонов с энергией E = hn.
Согласно квантовой теории явление рассеяния рентгеновского излучения можно рассматривать как результат упругого столкновения рентгеновского фотона с почти свободным электроном. При этом фотон передает электрону часть своей энергии и часть своего импульса в соответствии с законами сохранения энергии и импульса. Кинематика рассеяния рентгеновского фотона на свободном электроне показана на рис.4.
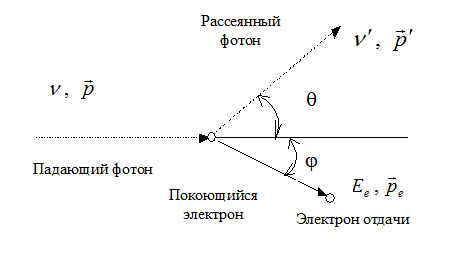
Рис. 4 - Кинематика комптоновского рассеяния на свободном электроне
Фотон с частотой n и энергией 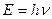 сталкивается с покоящимся электроном, масса которого равна
сталкивается с покоящимся электроном, масса которого равна 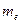 , а полная энергия электрона до столкновения или энергия покоя –
, а полная энергия электрона до столкновения или энергия покоя – 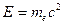 .
.
После столкновения возникает фотон с частотой 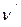 , движущийся под углом q к направлению движения первичного фотона, и электрона отдачи, обладающего энергией Ee и импульсом
, движущийся под углом q к направлению движения первичного фотона, и электрона отдачи, обладающего энергией Ee и импульсом 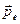 и образующий угол j с первичным направлением.
и образующий угол j с первичным направлением.
Закон сохранения энергии:
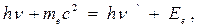 (1)
(1)
где 
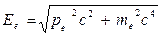 – полная энергия электрона отдачи в релятивистской механике,
– полная энергия электрона отдачи в релятивистской механике, 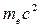 – полная энергия электрона до столкновения (энергия покоя),
– полная энергия электрона до столкновения (энергия покоя), 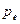 – импульс электрона, называемый после столкновения электроном отдачи.
– импульс электрона, называемый после столкновения электроном отдачи.
Закон сохранения импульса:
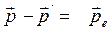 . (2)
. (2)
Вычитая квадрат второго выражения из квадрата первого (деленного на с), получаем
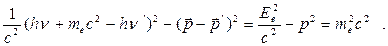 (3)
(3)
Поскольку
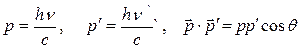 , (4)
, (4)
то решая ( 3 ) относительно 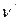 и введя длины волн
и введя длины волн 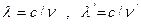 , получаем
, получаем
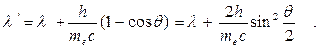 (5)
(5)
Или для величины смещения рассеянного излучения
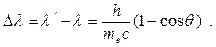 (6)
(6)
Величина
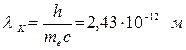
называется комптоновской длиной волны электрона.
Таким образом, мы видим, что с точки зрения квантовых представлений длина волны рассеянного излучения l` должна быть больше начальной. Это увеличение тем существеннее, чем больше угол рассеяния q. При рассеянии под заданным углом q величина Dl не зависит от длины волны l , поэтому эффект Комптона для длинноволнового излучения несущественен, т.е. относительное изменение длины волны мало Dl/l << 1, и, наоборот, большую роль для коротковолнового излучения, когда Dl/l » 1. В самом деле, для видимого света (l ~ 10-5 см):
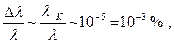
для рентгеновских же лучей (l ~ 10-8¸10-9 см):

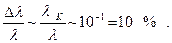
Кинетическая энергия электрона отдачи определяется выражением
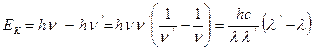 (7)
(7)
или
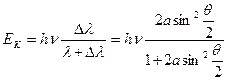 , (8)
, (8)
где 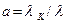 , а
, а 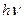 – энергия падающего фотона.
– энергия падающего фотона.
Импульс электрона отдачи равен
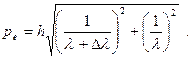 (9)
(9)
Энергия кванта, рассеянного на угол q, определяется выражением
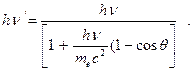 (10)
(10)
Из этой формулы следует, что при 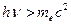 при малых углах рассеяния
при малых углах рассеяния 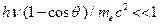 и энергия фотона мало изменяется при рассеянии
и энергия фотона мало изменяется при рассеянии 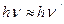 . При условии
. При условии 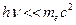 энергия фотона мало меняется практически для всех углов рассеяния.
энергия фотона мало меняется практически для всех углов рассеяния.
Для 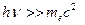 и больших углов рассеяния
и больших углов рассеяния
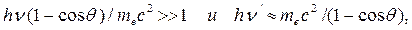
так что при q = p/2 энергия рассеявшегося фотона 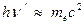 , а при q = p
, а при q = p 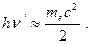
При уменьшении энергии hn` и, следовательно, импульса рассеянного фотона 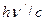 энергия и импульс электрона отдачи растут.
энергия и импульс электрона отдачи растут.
На рис.6 изображена векторная диаграмма распределения импульсов рассеянного кванта и электрона отдачи. Одинаковыми цифрами отмечены соответствующие импульсы рассеянного фотона и электрона отдачи.
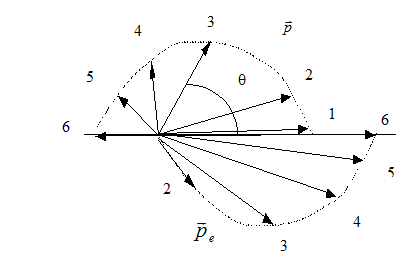
Рис. 5 - Векторная диаграмма распределение импульсов рассеянного кванта  и электрона отдачи
и электрона отдачи 
Дата добавления: 2015-09-29; просмотров: 1197;
