Описание метода измерения. При наложении двух или нескольких световых пучков наблюдается усиление света в одних точках пространства и ослабление в других
При наложении двух или нескольких световых пучков наблюдается усиление света в одних точках пространства и ослабление в других. Это явление называется интерференцией света. Устойчивую интерференционную картину могут давать только когерентные волны, т. е. такие, которые имеют одинаковую частоту и постоянную разности фаз. Для получения контрастной интерференционной картины необходимо также, чтобы интенсивности волн были соизмеримы и плоскости колебаний вектора напряженности электрического поля Е совпадали.
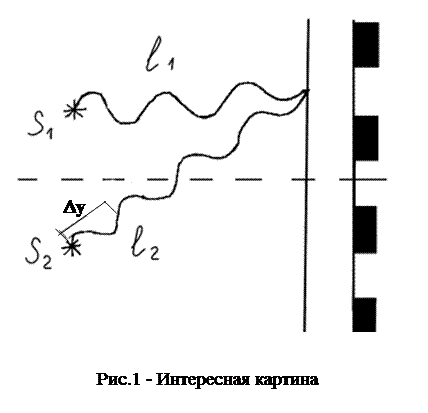
Один из методов получения когерентных волн основан на разделении на две части волны, излучаемой одним источником. Эти волны до попадания в заданную точку пространства проходят различные расстояния (или одинаковые расстояния в средах с различными показателями преломления). Между ними возникает постоянная разность фаз, вследствие чего получается интерференционная картина. Рис. 1.
 |
Если разность фаз 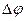 в данной точке пространства равна 2m
в данной точке пространства равна 2m 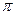 , где m - целое число, то в этом месте происходит усиление колебаний (максимум освещенности), если же разность фаз равна (2m+1)
, где m - целое число, то в этом месте происходит усиление колебаний (максимум освещенности), если же разность фаз равна (2m+1)  , то будет наблюдаться ослабление колебаний (минимум освещенности).
, то будет наблюдаться ослабление колебаний (минимум освещенности).
Оптической разностью хода двух световых лучей называется величина 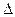 y = l1n1 – l2n2, где l1 l2 - геометрические пути, которые проходят первый и второй лучи в средах с показателями преломления n1 и n2 соответственно.
y = l1n1 – l2n2, где l1 l2 - геометрические пути, которые проходят первый и второй лучи в средах с показателями преломления n1 и n2 соответственно.
Оптическая разность хода 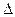 y связана с разностью фаз
y связана с разностью фаз 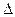
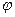 соотношением
соотношением
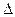 y =
y = 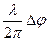 , (1)
, (1)
что позволяет получить условия максимума и минимума в виде
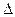 y = m
y = m 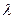 , (2)
, (2)
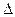 y = (2m+1)
y = (2m+1) 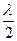 , (3)
, (3)
где 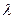 - длина волны интерферирующего света, m = 0, 1, 2, 3… - порядок полосы. Следует отметить, что интерференция будет наблюдаться, если оптическая разность хода не превышает длину когерентности излучения. Длина когерентности есть такая оптическая разность хода между интерферирующими волнами, при которой случайное изменение фазы достигает величины ~
- длина волны интерферирующего света, m = 0, 1, 2, 3… - порядок полосы. Следует отметить, что интерференция будет наблюдаться, если оптическая разность хода не превышает длину когерентности излучения. Длина когерентности есть такая оптическая разность хода между интерферирующими волнами, при которой случайное изменение фазы достигает величины ~ 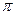 . С увеличением номера полосы m разность хода растет, вследствие чего ухудшается четкость интерференционной картины. Длина когерентности lког для не лазерных источников света представляет величину порядка нескольких сантиметров и меньше. В случае лазерных источников lког достигает 1000 м и выше.
. С увеличением номера полосы m разность хода растет, вследствие чего ухудшается четкость интерференционной картины. Длина когерентности lког для не лазерных источников света представляет величину порядка нескольких сантиметров и меньше. В случае лазерных источников lког достигает 1000 м и выше.
Когерентными источниками в опытах по интерференции света могут быть источник света и его изображение в зеркале (опыт Лойда), два мнимых изображения источника света, которые дают два зеркала или бипризма (опыт Френеля). В опыте Юнга по интерференции света источниками были два отверстия, освещенные светом одного источника. Следовательно, для создания когерентных волн нужно свет от одного источника разделить на два пучка и направить в точку наблюдения разными путями.
В предлагаемой лабораторной работе интерференционную картину получают следующим образом. Если осветить плоско – выпуклую линзу плоской световой волной с большой длиной когерентности (от лазерного источника), то эта волна частично отразится как от передней выпуклой поверхности, так и от задней плоской поверхности линзы. Две отраженные волны интерферируют друг с другом и интерференционную картину в виде концентрических темных и светлых колец можно наблюдать на экране (рис. 2). Поскольку линза является аксиально-симметричным стеклянным клином, то эти кольца являются примером полос равной толщины. Радиусы колец rm зависят от радиуса кривизны линзы R и расстояния между линзой и экраном L.


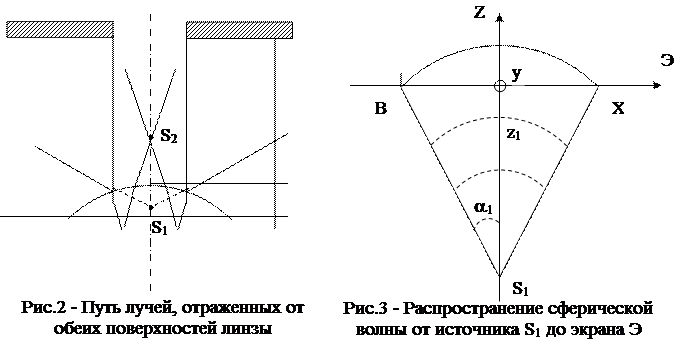
Таким образом, измерив радиусы интерференционных колец и расстояние между линзой и экраном, можно определить радиус кривизны линзы. Поскольку диаметр лазерного пучка обычно много меньше размеров линзы, то при выводе рабочей формулы можно использовать приближение параксиальных лучей, т.е. лучей, проходящих вблизи главной оси линзы. В этом приближении все углы a можно считать малыми, т.е. sin 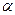

 , а cosa
, а cosa 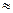 1-a2/2 В параксиальном приближении интерференционная картина на экране может рассматриваться как результат интерференции двух сферических волн от источников, расположенных в точках S1 и S2 (рис. 2). Уравнение поверхности разных фаз волны распространяющейся из точки S записывается следующим образом:
1-a2/2 В параксиальном приближении интерференционная картина на экране может рассматриваться как результат интерференции двух сферических волн от источников, расположенных в точках S1 и S2 (рис. 2). Уравнение поверхности разных фаз волны распространяющейся из точки S записывается следующим образом:
x2 + y2 + z2 = l21, (4)
где l1 - расстояние от точки S1 до точки B на экране, x, y, z – декартовы координаты точки В (рис. 3). Если сферическая волна распространяется в пределах некоторого телесного угла, ось которого совпадает с осью z, то в параксиальном приближении
l1 = 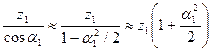 , (5)
, (5)
где 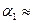 r/z1, z1 - расстояние от источника S1 до экрана, r =
r/z1, z1 - расстояние от источника S1 до экрана, r = 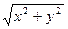 . Таким образом
. Таким образом
l1 = z1 + 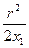 (6)
(6)
Аналогично для волны, распространяющейся из точки S2, получаем
l2 = z2 + 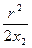 (7)
(7)
Если оптическая разность хода
l1 - l2 = m 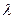 , (8)
, (8)
то в точке В будет наблюдаться максимум интерференционной картины, т.е. светлое кольцо.
Для определения положения мнимых источников S1 и S2 относительно вершины линзы О, рассмотрим луч 1, проходящий на некотором малом расстоянии а от оси линзы (рис. 4а). Этот луч отразится от поверхности линзы под углом 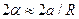 к оси. Продолжая отраженный луч на рис. 4а в обратную сторону до пересечения с осью в точке S1, получаем
к оси. Продолжая отраженный луч на рис. 4а в обратную сторону до пересечения с осью в точке S1, получаем
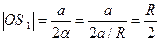 . (9)
. (9) 
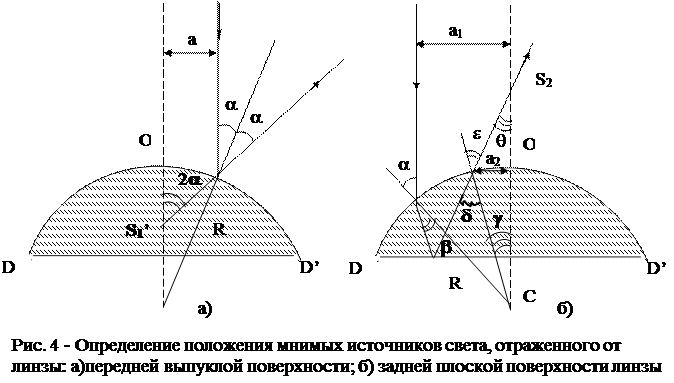
Несколько сложнее определяется положение второго источника S2 (рис. 4б). Поскольку линза имеет конечную толщину, то луч попав в нее и отразившись от плоской грани, выходит уже на другом расстоянии от оси. Из рис. 4б видно, что
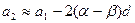 , (10)
, (10)
где 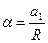
 угол падения,
угол падения, 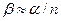 - угол преломления, d - толщина линзы вблизи оси. Предполагается, что n = sin
- угол преломления, d - толщина линзы вблизи оси. Предполагается, что n = sin 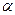 /sin
/sin 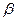
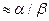 . Отразившись от плоской поверхности DD\, луч падает на выпуклую поверхность под углом
. Отразившись от плоской поверхности DD\, луч падает на выпуклую поверхность под углом 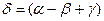 , где
, где 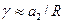 , а после преломления угол
, а после преломления угол 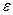 преломленного луча с нормалью к поверхности станет равным
преломленного луча с нормалью к поверхности станет равным 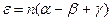 .Поскольку нормаль к поверхности линзы в точке выхода луча составляет угол
.Поскольку нормаль к поверхности линзы в точке выхода луча составляет угол 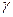 с главной осью линзы, то угол между вышедшим лучом и главной осью линзы будет равен
с главной осью линзы, то угол между вышедшим лучом и главной осью линзы будет равен 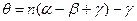 . Используя выражение (10) и учитывая, что
. Используя выражение (10) и учитывая, что 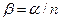 согласно закону Снеллиуса, находим
согласно закону Снеллиуса, находим
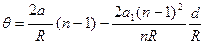 . (11)
. (11)
Теперь можно окончательно определить положение второго мнимого источника S2:
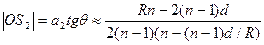 (12)
(12)
Выражение (12) достаточно сложное, однако существуют предельные случаи, в которых его можно существенно упростить.
1. Тонкая линза (d<<R):
 . (13)
. (13)
В этом случае
z1 = L – R/2(n - 1), (14)
z2 = L + R/2, (15)
где L - расстояние от вершины линзы до экрана. Подставляя z1 и z2, в уравнение (6)-(8) получаем:
 . (16)
. (16)
При наблюдении интерференционной картины на большом расстоянии от линзы L>>R:
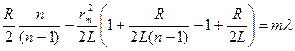 (17)
(17)
После несложных алгебраических преобразований получаем
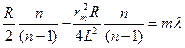 . (18)
. (18)
Отсюда
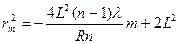 . (19)
. (19)
Знак «-» в формуле (19) объясняется тем, что нумерация колец в данной задаче ведется в обратном порядке, т.е. кольцо с минимальным радиусом имеет максимальный номер, соответствующий наибольшей разности хода. Построив зависимость 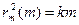 , где k это tg угла наклона графика к оси m, можно определить радиус кривизны линзы по наклону прямой
, где k это tg угла наклона графика к оси m, можно определить радиус кривизны линзы по наклону прямой 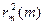 (рис. 5). Таким образом
(рис. 5). Таким образом
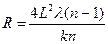 . (20)
. (20)
2. Полусферическая линза (d=R):
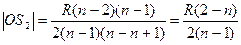 . (21)
. (21)
В случае полусферической линзы (d = R) из (8) получаем
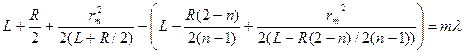 . (22)
. (22)
Для L>>R, проводя преобразования, аналогичные случаю тонкой линзы, получаем
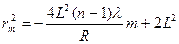 , (23)
, (23)
откуда окончательно определяем R:
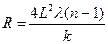 . (24)
. (24)
Таким образом, зная длину волны лазерного излучения 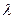 и показатель преломления стекла n, а также измерив расстояние L, можно определить радиус кривизны плоско – выпуклой линзы.
и показатель преломления стекла n, а также измерив расстояние L, можно определить радиус кривизны плоско – выпуклой линзы.
Использование явления интерференции позволяет решать различные технические задачи. На этом явлении основана работа антенн радиотелескопов, использующихся для определения положения источников радиоволн на небе и их угловых размеров.
Дата добавления: 2015-09-29; просмотров: 826;
