Свойства арккотангенса
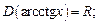
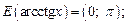
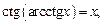 где
где 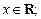
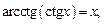 где
где 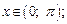
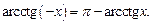
График функции 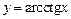 приведен на рис. 7.18.
приведен на рис. 7.18.
 |
Рис. 7.18
Для обратных тригонометрических функций выполняются следующие равенства:
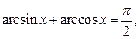
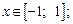 (7.16)
(7.16)
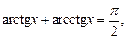
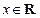 (7.17)
(7.17)
Пример 1.Проверить, справедливы ли равенства:
1) 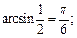 2)
2) 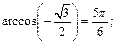
3) 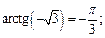 4)
4) 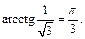
Решение.1) 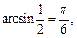 так как
так как 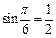 и
и 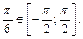 Равенство верно.
Равенство верно.
2) 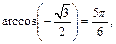 так как
так как 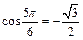 и
и 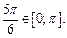 Равенство верно.
Равенство верно.
3) 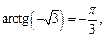 так как
так как 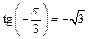 и
и 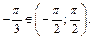 Равенство верно.
Равенство верно.
4) 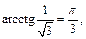 так как
так как 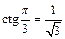 и
и 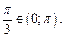 Равенство верно.
Равенство верно.
Пример 2.Вычислить
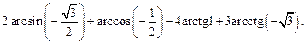
Решение.Вычислим слагаемые отдельно, чтобы прокомментировать действия.
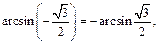
функция нечетная и
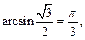 так как
так как 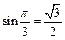 и
и 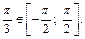
Поэтому 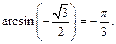
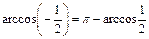 (по свойству) и
(по свойству) и 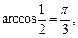
так как 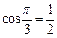 и
и 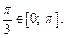
Поэтому 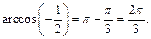
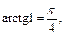 так как
так как 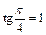 и
и 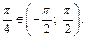
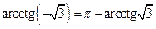 (по свойству) и
(по свойству) и 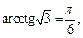
так как 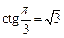 и
и 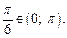
Поэтому 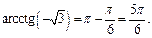
Таким образом,
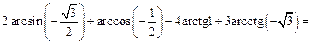
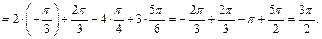
Получаем ответ: 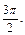
Пример 3.Решить уравнение 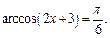
Решение.Поскольку 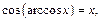 то
то
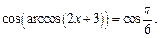 т. е.
т. е. 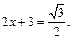
Находим:
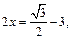
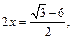
откуда приходим к ответу 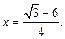
Пример 4.Найти область значений функции 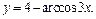
Решение. Поскольку 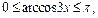 то
то
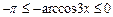 и
и 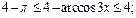
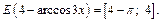
Получаем ответ: 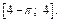
Пример 5.Вычислить 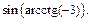
Решение.Используя свойство функции 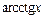 для отрицательного аргумента и формулу приведения для
для отрицательного аргумента и формулу приведения для 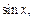 получаем:
получаем:
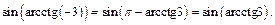
Для дальнейших вычислений необходимо выразить функцию 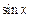 через
через 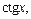 чтобы воспользоваться затем формулой
чтобы воспользоваться затем формулой
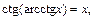
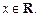
Из формулы 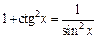 выражаем
выражаем
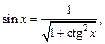 если
если 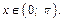
Для нашего случая имеем:
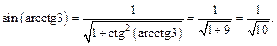
Получаем ответ: 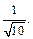
Пример 6. Построить график функции 
Решение. Для построения будем использовать правила преобразования графика функции 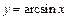 (рис. 7.15).
(рис. 7.15).
Рассмотрим последовательность преобразований, позволяющих из графика функции 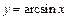 получить график заданной функции. Преобразуем данную функцию следующим образом:
получить график заданной функции. Преобразуем данную функцию следующим образом:
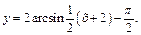
Выполним построение поэтапно.
 1. График функции
1. График функции 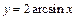 может быть получен из графика
может быть получен из графика 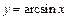 (рис. 7.15) путем растяжения вдоль оси Оу в 2 раза (рис. 7.19).
(рис. 7.15) путем растяжения вдоль оси Оу в 2 раза (рис. 7.19).
Рис. 7.19
2. График функции 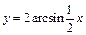 может быть получен из графика функции
может быть получен из графика функции 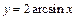 путем растяжения вдоль оси Ох в 2 раза (рис. 7.20).
путем растяжения вдоль оси Ох в 2 раза (рис. 7.20).

Рис. 7.20
3. График функции 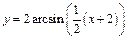 может быть получен из графика функции
может быть получен из графика функции 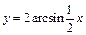 путем параллельного переноса вдоль оси Ох на 2 единицы влево (рис. 7.21).
путем параллельного переноса вдоль оси Ох на 2 единицы влево (рис. 7.21).
 |
Рис. 7.21
4. График функции 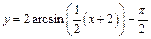 получаем из графика
получаем из графика 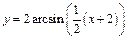 путем параллельного переноса вдоль оси Оу на
путем параллельного переноса вдоль оси Оу на 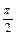 единиц вниз (рис. 7.22).
единиц вниз (рис. 7.22).
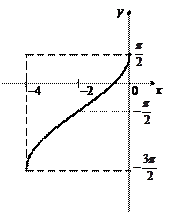 |
Рис. 7.22
Пример 7. Построить на единичной окружности угол a, такой, что
1) 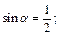 2)
2) 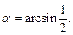
Решение. 1) Воспользуемся определением синуса. Равенству  соответствуют два угла
соответствуют два угла 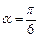 и
и 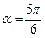 (рис. 7.23).
(рис. 7.23).
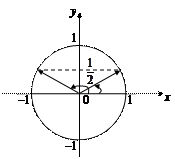 |
Рис. 7.23
 2) По определению арксинуса
2) По определению арксинуса 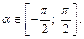 На данном промежутке существует только один угол, синус которого равен
На данном промежутке существует только один угол, синус которого равен 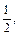 т. е.
т. е. 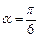 (рис. 7.24).
(рис. 7.24).
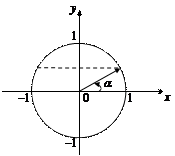 |
Рис. 7.24
Пример 8. Решить уравнение 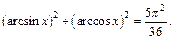
Решение.Формула (7.16) позволяет перейти к системе
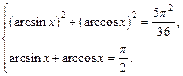 (7.18)
(7.18)
Пусть 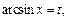
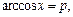 где
где 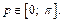 Тогда система (7.18) приобретает вид:
Тогда система (7.18) приобретает вид: 
Решим последнюю систему и получим: 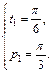 или
или 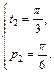
Отсюда 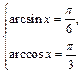 или
или 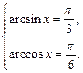
Обе эти системы имеют решение. Из первой системы получаем 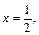 а вторая дает
а вторая дает 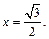
Получаем ответ: 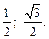
Дата добавления: 2015-09-29; просмотров: 735;
