Основные формулы гидравлического расчета магистрального трубопровода. Напорная характеристика трубопровода

Закономерность изменения напора в трубопроводе находится при помощи решения уравнений установивщейся движении потока жидкости, ее решение:

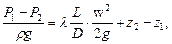(47)

здесь L - длина трубопровода, D - внутренний диаметр его трубы, w- скорость потока, λ - коэффициент гидравлического сопротивления, P₁, z₁ и P₂, z₂- давление и нивелирные высоты начального и конечнего пунктов трубопровода. Тогда 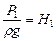- будет начальным напором, 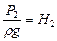- конечным напором.

- (48)

-это уменьшение напора в трубопроводе, ее называет полным потерем напора в трубопроводе (уменьшение). Согласно формуле (47) полные потери напора в трубопроводе состоит из двух слагаемых:

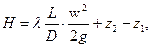(49)

Первая из них 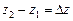- разность нивелирных высот. Вторую из них:

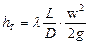- (50)

называет потери напора от трения. (50)-формула называется формулой Дарси-Вейсбаха. Тогда

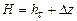, (51)

то, есть полные потери напора в трубопроводе состоит из потери напора от трения и от потери напора, необходимого для подъема жидкости на высоту .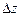

Коэффициент гидравлического сопротивления от трения λ зависит от режима течения. Для его нахождения определяется средняя скорость потока течения жидкости в трубопроводе:

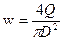. (50)

Этот скорость определяет число Рейнольдса:

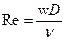, (51)

где ν - кинематическая вязкость жидкости, она связана с динамической вязкостью:

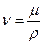. (52)

Если Re≤2320, то течение ламинарное, а при Re>2320, течение турбулентное.

Для ламинарного течения справедлив закон Стокса:

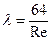. (53)

Для турбулентного течения различаются три зоны течения жидкости, и соответственно используются три различных закона для коэффициента гидравлического сопротивления от трения. Граница зон определяется переходным числом Рейнольдса:

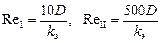. (54)

здесь k_э-шероховатость внутренней стенки трубы. Ее приблизительные значения следующие: для безшовных стальных труб k_э=0,014мм; для сварных стальных труб: если новый-0,05мм, через нескольких лет-0,20мм, после очистки-0,15мм, умеренно заржавленные-0,5мм, старые заржавленные -1мм, сильно заржавленные -3мм.

Если 2320<Re<Re_I, то коэффициента гидравлического сопротивления от трения определяется по формуле Блазиуса (при ):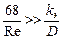

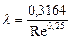. (55)

Если Re_I ≤ Re < Re_II, то коэффициента гидравлического сопротивления от трения определяется по формуле Альтшуля:

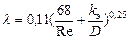. (56)

Если Re≥ Re_II, то коэффициента гидравлического сопротивления от трения определяется по формуле Шифринсона ( ):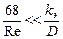

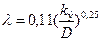. (57)

Причина три зоны турбулентного течения состоит в следующем. При прохождений жидкости по трубопроводу в турбулентном режиме напор (давление) жидкости уменьшается в основном по двум причинам: разные слои потока движутся с неодинаковыми скоростями и шероховатость стенки трубы мешает движению потока. Эти две причины определяет режим турбулентных течении и делят ее на 3 зоны. 1-зона есть зона гидравлически гладких труб (сопративление из-за 1-причины, определяется только числом Рейнольдса, формула Блазиуса при 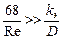и 2320<Re<Re_I). 2-зона есть зона смешанного трения (на сопротивления влияют обе причины, оно определяется числом Рейнольдса и шероховатостью внутренней стенки трубы, формула Альтшуля при Re_I ≤ Re < Re_II) и 3-зона - зона квадратичного закона трения (сопративление из-за 2-причины, определяется только шероховатостью внутренней стенки трубы формула Шифринсона при 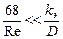и Re≥ Re_II).

Этих трех формул можно обобщить таким образом:

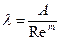. (58)

Эта формула есть формула Лейбензона, а А и т - называются коэффициентами Лейбензона. Коэффициенты Лейбензона заданы в следующей таблице.

3-таблица. Коэффициенты Лейбензона.

Re	m	A	β
Re ≤2320			4,15
2320< Re ≤ Re_I	0,25	0,3164	0,0246
Re_I ≤ Re < Re_II	0,123	0,236	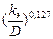0,0802А
Re≥ Re_II		λ	0,0827 λ

Тогда потери напора от трения с учетом формул (50), (51) и (58):

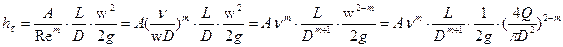
и после объеднинение одинаковых членов получаем:

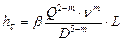. (59)

Эта формула называется обобщенной формулой Лейбензона;

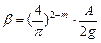. (60)

Обобщенная формула Лейбензона удобна тем, что она одинакова во всех зонах течения и удобна для математических операции. Она также наглядно показывает вид зависимости потери напора от расхода жидкости, от кинематической вязкости жидкости и от диаметра трубы.

Профиль трассы (рис. 3) используют при определении расчетной длины трубопровода и разности геодезических высот. На профиле ведется расстановка нефтеперекачивающих станций (НПС). Профиль-чертеж, на котором отложены и соединены между собой характерные точки трассы. Расстояния от начального пункта и геодезические высоты этих точек - их координаты. Таким образом, расстояние между какими-либо двумя точками определяется не длиной соединяющей их линии, а ее проекцией на ось абсцисс. Иными словами, расстояния на профиле откладываются по горизонтали. Это очень важно иметь в виду.

Профиль трассы вычерчивается сжатым: масштаб по вертикали крупнее, чем по горизонтали. Поэтому все возвышенности и впадины на трассе выступают резко, чертеж получается наглядным.

Отложим вверх по вертикали от начальной и конечной точек профиля трассы напоры 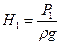и 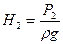(рис. 3). Концы полученных отрезков соединим прямой. Полученная линия аназывается линией гидравлического уклона.

Она показывает распределение напоров (а, следовательно, и давлений) по длине трубопровода. Линия гидравлического уклона показывает, что, как уменьшается напор по трубопроводу. Например, в точке М напор Н_М< Н₁, а давление равно P_М=ρgН_М. Тангенс угла наклона α этой прямой называется гидравлическим уклоном i, то есть i =tg α. Предполагается, что диаметр трубопровода - одинаковый по всей длине, местных сопротивлений нет, расход по длине не изменяется. Из чертежа видно, что

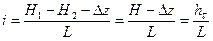. (61).

Следовательно, физический смысл гидравлического уклона - потеря напора на трение, приходящаяся на единицу длины трубопровода. То, есть, гидравлический уклон есть отношение потери напора от трения к длине трубопровода.

Согласно формуле Дарси-Вейсбаха гидравлический уклон равен:

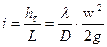, (62)

Согласно обобщенной формуле Лейбензона:

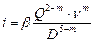, (63)

или

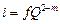, (64)

где 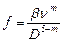. Эта формула наглядно показывет изменение гидравлического уклона в зависимости от пропускного способности трубопровода.

Потери напора по всей длине трубопровода при помощи гидравлического уклона находится в таком виде:

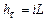и 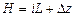. (65)

Гидравлический уклон на различных участках трубопровода может быть разным в зависимости диаметра, или в зависимости от изменения вязкости горячей нефти при горячей перекачке (рис. 4).

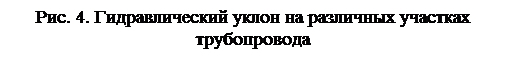
Зависимость суммарного потери напора по всей длине трубопровода (с учетом местных потерь и потери при перекачке нефти на резервуары в конечных пунктах эксплуатационных участков) от пропускной способности трубопровода называется напорной (рабочей) характеристикой трубопровода. Таким образом для насосных станций напорная характеристика есть зависимость развиваемого напора, а для трубопровода - потерянного напора от пропускной способности.

Напорная (рабочая) характеристика трубопровода получается в аналитическом виде только в случае использования обобщенной формулой Лейбензона. Если Н_кп- остаточный напор в конечных пунктах эксплуатационных участков (этот напор расходуется при перекачке нефти в резервуары), то

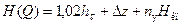, (68)

где 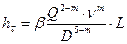, 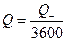; коэффициент 1,02 учитывают потери напора в местных сопротивлениях (в ответвлениях трубопровода, на задвижках, и т. д.).

Обычно обобщенная формула Лейбензона для решение практических задач редько используется из-за приближенного характера. Если использовать более точную формулу Дарси-Вейсбаха, то напорная характеристика трубопровода в аналитическом виде не получается. Тогда эта характеристика можно получить в виде таблицы, или графика. Для получения такой напорной характеристики трубопровода берем несколько значений пропускной способности, расположенных вокруг среднего значения Q_ч.ср ( например, если Q_ч.ср =1330 м³ /час, то берем Q_ч =1200,1300,1400,1500 м³ /час) и для всех этих значений найдем полные потери напора в трубопроводе в следующей последовательности. Берем, например берем Q_ч =1200 м³ /час. Найдем:

1. 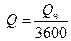- значение секундного объемного расхода;

2. 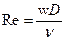- число Рейнольдса;

3. 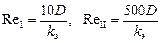- переходным числом Рейнольдса;

здесь k_э-шероховатость внутренней стенки трубы, обычно для задач k_э=0,2мм;

4. Если 2320<Re<Re_I, то ,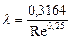

если Re_I ≤ Re < Re_II, то ,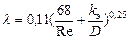

если Re≥ Re_II, то 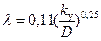- коэффициент гидравлического сопротивления от трения;

5. 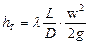- потери напора от трения по формуле Дарси-Вейсбаха;

6. 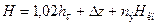- полные потери напора в трубопроводе при пропускной способности Q_ч.

Далее к каждому из вышевыбранному значению Q_ч используем эти же формулы и алгоритм, получаем несколько значений H=H(Q_ч). Заполним таблицу значений H=H(Q_ч). Из полученных значений в милиметровке строим график функции H=H(Q_ч). Эта - напорная характеристика трубопровода.

В следующий очередь там же строим график функции H_нпс= H_нпс(m_н, Q_ч) при помощи (66) для различных количеств работающих основных насосов m_н=3п, m_н=3п-1и m_н=3п-2 (получается 3 графика). Эта - напорная характеристика НПС. Если напорных характеристик трубопровода и НПС будем строить вместе (в одной милиметровке), то получается совмещенная характеристика (рис. 5).

Напорные характеристики трубопровода и НПС в данной задаче пересекаются в трех точках (Q_ч1, Q_ч2, Q_ч3). Эти точки показывают фактических пропускных способностей трубопровода при работе 3п-2, 3п-1, 3п числа магистральных насосов. В качестве рабочей точки Q_р берется самая близкая точка к среднему значению Q_ч.ср и не меньшей ее: Q_чi≥ Q_ч.ср (i=1,2,3). То, есть трубопровод будет работать с такой пропускной способностью. То есть рабочая точка – это такое значение пропускной способности, когда потери напора ровно равны развиваемым всеми насосами напору. Она (так называемая рабочая точка Q_р) соответствует точному решению уравнении при целом п:

H_нпс(3п, Q_р)=H(Q_р), (69)

Это трансцендентное уравнение решается графическим способом, или при промощи компьютерных программ.

Задачу без построения графика можно приближенно решить следующим образом:

- взять 2 значения подачи Q_ч₁и Q_ч₂вокруг Q_ч_.ср таким образом, что Q_ч₁≤ Q_ч_.ср и Q_ч₂≥ Q_ч_.ср (например: пусть Q_ч_.ср=1330 м³/ч, тогда Q_ч₁=1300 м³/ч и Q_ч₂=1400 м³/ч).

- найти H₁= H(Q_р1), H₂= H(Q_р2), H_нпс1=H_нпс(m_н, Q_р1) и H_нпс2=H_нпс(m_н, Q_р2). Тогда

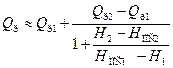. (180)

Точность полученного решения можно повысить, если взять 2 новые значения подачи Q_ч₁и Q_ч₂вокруг найденного Q_р и использовать (34) еще раз (метод итерации).

В рассматриваемых формулах есть только разность нивелирных высот начального и конечнего пунктов трубопровода, а профиль трассы и высота промежуточных точек не входит в эти формулы. Поэтому расчеты не учитывает особенности промежуточных точек. Возвышенность на трассе, от которой нефть приходит на конечный пункт нефтепровода самотеком, называется перевальной точкой. Таких точек может быть несколько (рис. 6).

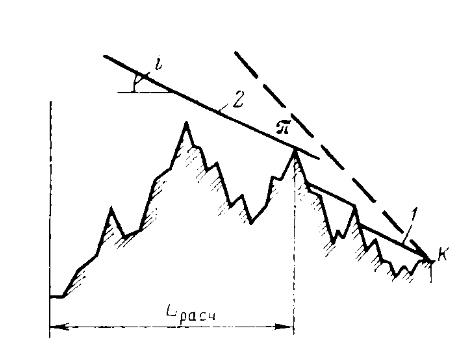
Расстояние от начального пункта нефтепровода до ближайшей из них я называется расчетной длиной нефтепровода. При гидравлическом расчете длина нефтепровода принимается равной расчетной, разность отметок 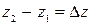- равной превышению перевальной точки над начальным пунктом трассы. Для нахождения перевальной точки проведем от конечного пункта трассы К линию гидравлического уклона 1 до пересечения ее с профилем. Затем вычертим параллельную линию 2 с расчетом, чтобы она касалась профиля, нигде его не пересекая. Место касания линии гидравлического уклона 2 с профилем трассы - перевальная точка π, определяющая расчетную длину нефтепровода. Если линия гидравлического уклона, проведенная из конечной точки трассы, нигде не пересекается с профилем и не касается его (на рис. 6 -пунктирная линия), перевальная точка отсутствует и расчетная длина равна полной длине нефтепровода. Перевальная точка может оказаться не только между последней станцией и конечным пунктом нефтепровода, но и на перегоне между промежуточными НПС. При соответствующем профиле перевальная точка может появиться при изменении режима работы нефтепровода (тогда линия гидравлического уклона изменяется): при отключении какой-либо станции или при изменении вязкости перекачиваемой нефти.

Рассмотрим движение нефти за перевальной точкой. Как видно из рис.7, разность высот точек π и С, равная (πN), больше потери напора на трения (πK)на этом участке, поэтому скорость течения жидкости в участке π-С увеличивается. Если скорость увеличивается, то из уравнения сплошности Q=wF видно, что с увеличением скорости живое сечение потока F должно уменьшаться и становится меньше, чем поперечное сечение трубы, в результате чего в трубе появляется пустое пространство. Пространство, свободное от нефти, будет занято выделившимися из нее парами и растворенными газами. Во избежание разрыва сплошности потока на конечном пункте (или на НПС, куда приходит нефть с перевальной точки) следует поддерживать давление, обеспечивающее некоторый запас напора на перевальной точке. Обычно этот запас принимают равным 10 м.

<1 234 5 6 7 >

Дата добавления: 2015-09-28; просмотров: 12396;