Примеры решения задач. Задача 1. Зависимость пройденного телом пути от времени выражается уравнением ( = 2 м/с, = 3 м/с2
Задача 1. Зависимость пройденного телом пути 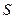 от времени
от времени 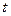 выражается уравнением
выражается уравнением 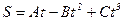 (
( 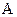 = 2 м/с,
= 2 м/с, 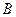 = 3 м/с2,
= 3 м/с2, 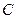 = 5 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени
= 5 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени 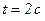 после начала движения пройденный путь, скорость и ускорение.
после начала движения пройденный путь, скорость и ускорение.
Дано:
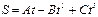 ; ;
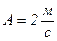 ; ;
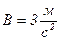 ; ;
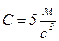 ; ;
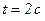 . .
| Решение:
Для определения зависимости скорости движения тела от времени определяем первую производную от пути по времени:
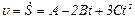 ,
или после подстановки ,
или после подстановки
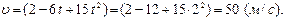 Для определения зависимости ускорения движения тела от времени определяем первую производную от скорости по времени: Для определения зависимости ускорения движения тела от времени определяем первую производную от скорости по времени:
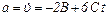 ,
или послеподстановки ,
или послеподстановки
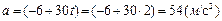 .
Пройденный путь определяется как разность .
Пройденный путь определяется как разность
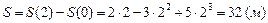 . .
|
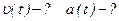 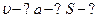
|
Ответ: 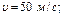
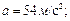
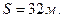
Задача 2.Тело брошено со скоростью 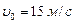 под углом
под углом 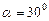 к горизонту. Принимая тело за материальную точку, определите нормальное
к горизонту. Принимая тело за материальную точку, определите нормальное 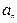 и тангенциальное
и тангенциальное 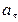 ускорение тела через 1,2 с после начала движения.
ускорение тела через 1,2 с после начала движения.
Дано:
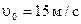 ; ;
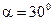 ; ;
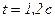 ; ;
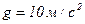 . .
| Решение
Построим чертеж и определим проекции
скорости 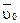 в начальный момент времени: в начальный момент времени:
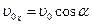 , , 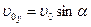 . .
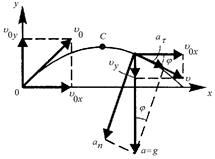
Рис.1.1 | ||
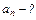
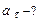
|
Проекция 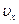 в процессе движения точки остается постоянной по величине и направлению.
в процессе движения точки остается постоянной по величине и направлению.
Проекция 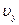 на ось
на ось 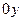 изменяется. В точке С (рис 1.1) скорость направлена горизонтально, т.е.
изменяется. В точке С (рис 1.1) скорость направлена горизонтально, т.е. 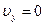 . Это означает, что
. Это означает, что 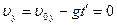 , где
, где 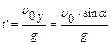 - время, в течение которого материальная точка поднимается до максимальной высоты, или после подстановки
- время, в течение которого материальная точка поднимается до максимальной высоты, или после подстановки 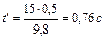 .
.
К моменту времени 1,2 с тело будет находиться на спуске. Полное ускорение в процессе движения направлено вертикально вниз и равно ускорению свободного падения 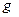 . Нормальное ускорение равно проекции ускорения свободного падения на направление радиуса кривизны, а тангенциальное ускорение - проекции ускорения свободного падения на направление скорости движения (см. рис.1.1).
. Нормальное ускорение равно проекции ускорения свободного падения на направление радиуса кривизны, а тангенциальное ускорение - проекции ускорения свободного падения на направление скорости движения (см. рис.1.1).
Из треугольников скоростей и ускорений имеем:
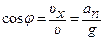 ,
, 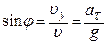 ,
,
откуда 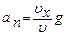 ,
, 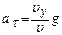 ,
,
где 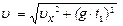 - скорость в момент времени
- скорость в момент времени 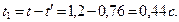
После подстановки получаем:
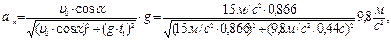
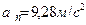 .
.
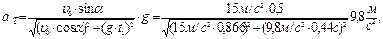
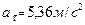 .
.
Ответ: 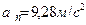 ,
, 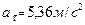 .
.
Задача 3. Колесо автомобиля вращается равнозамедленно. За время 2 мин оно изменило частоту вращения от 240 до 60 мин-1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
Дано:
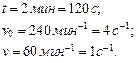
| Решение:
Запишем формулы для угла поворота и угловой скорости при равнозамедленном вращении:
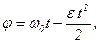 (1) (1)
|
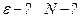
| 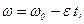 (2) (2)
|
где 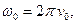
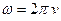 - угловые скорости в начальный и конечный моменты времени соответственно.
- угловые скорости в начальный и конечный моменты времени соответственно.
Из уравнения (2) получаем:
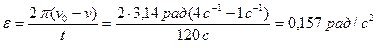 .
.
Угол поворота 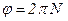 . Поэтому выражение (1) можно записать так:
. Поэтому выражение (1) можно записать так: 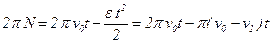 .
.
Отсюда: 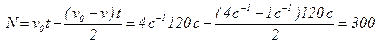 .
.
Ответ: 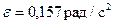 ;
; 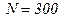 .
.
Задача 4.Точка движется по окружности радиусом 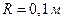 так, что зависимость угла поворота радиуса от времени дается уравнением
так, что зависимость угла поворота радиуса от времени дается уравнением 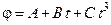 , где
, где 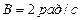 ,
, 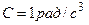 . Определите к концу второй секунды вращения: а) угловую скорость; б) линейную скорость; в) угловое ускорение; г) нормальное ускорение; д) тангенциальное ускорение.
. Определите к концу второй секунды вращения: а) угловую скорость; б) линейную скорость; в) угловое ускорение; г) нормальное ускорение; д) тангенциальное ускорение.
Дано:
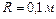 ; ; 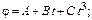 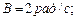 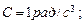 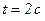 . .
| Решение:
Зависимость угловой скорости от времени определяем, взяв первую производную от угла поворота по времени, т.е. 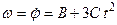 .
Для момента времени .
Для момента времени  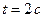
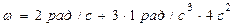 , , 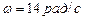 .
Линейная скорость точки .
Линейная скорость точки 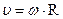 , или после подстановки , или после подстановки 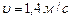 . .
|
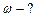 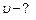
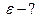 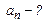 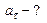
| |
Зависимость углового ускорения точки от времени определится первой производной от угловой скорости по времени, т.е. 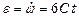 .
Для момента времени .
Для момента времени 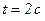 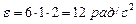 . Нормальное и тангенциальное ускорения определяются по формулам соответственно: . Нормальное и тангенциальное ускорения определяются по формулам соответственно:
| |
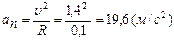 и
и 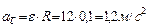 .
Ответ: .
Ответ: 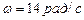 ; ; 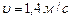 ; ; 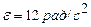 ; ;
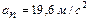 ; ; 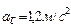 . .
|
Дата добавления: 2015-09-28; просмотров: 954;
