Составляющие теплообмена земной поверхности
Глава 3. Тепловой баланс и термический режим
Земной поверхности
Составляющие теплообмена земной поверхности
Поверхность по определению не имеет ни объема, ни массы, она не может накапливать теплоту или иную субстанцию. Следовательно, сумма потоков любых субстанций, приходящих к поверхности (сверху или снизу) равна сумме потоков субстанций, уходящих от этой поверхности.
Пусть потоки субстанций, приходящих к поверхности, считаются положительными, а потоки, уходящие от неё, – отрицательными. Уравнение баланса потоков субстанций для рассматриваемой поверхности примет вид:
ΣSi=0, (3.1)
т.е. алгебраическая сумма потоков равна нулю, где Si – i-ый поток субстанции.
С точки зрения баланса тепла для любого участка земной поверхности это означает, что за любой промежуток времени от поверхности уходит вверх и вниз в совокупности такое же количество тепла, какое за это время к ней приходит сверху и снизу.
Выше мы показали, что разница между поглощенной радиацией и эффективным излучением равна радиационному балансу (В). Радиационный баланс связан с радиационным теплообменом,т.е. с переносом тепла коротковолновой и длинноволновой радиации.
Теплообмен земной поверхностью и атмосферой (А). Земная поверхность может получать или терять тепло также за счет механизмов теплопроводности, т.е. путем теплообмена между земной поверхностью и атмосферой. Если температура приземной атмосферы больше температуры земной поверхности, то поток тепла А направлен из атмосферы к поверхности, в противном случае – от поверхности к атмосфере. Теплопоток А называют турбулентным теплообменом поверхности с атмосферой. Он осуществляется при участии атмосферной турбулентности, представляющей многочисленные беспорядочно движущиеся вихри, резко ускоряющие передачу тепла. Турбулентный теплообмен усиливается при увеличении скорости ветра, и с возрастанием разницы температуры воздуха и земной поверхности. Молекулярный теплообмен в приземной атмосфере ничтожно мал по сравнению с турбулентным.
Адвекция (от лат. Advectio – доставка) – в метеорологии перемещение воздуха в горизонтальном направлении и перенос вместе с ним его свойств, например, температуры и влажности. В этом смысле говорят об адвекции тепла и холода. Адвекция холодных и тёплых, сухих и влажных воздушных масс играет важную роль в метеорологических процессах и, тем самым, влияет на состояние погоды. Так, тепло, переносимое из экваториальных и субэкваториальных широт в умеренные и полярные страны, способствует снижению там суровости климата, особенно в зимние сезоны года. Адвективное тепло поступает из атмосферы к земной поверхности в результате турбулентного теплообмена с атмосферой.
Конвекция(от лат. convectio – принесение, доставка), вертикальные перемещения объёмов воздуха с одних высот на другие, обусловленные тем, что воздух более тёплый и, следовательно, менее плотный, чем окружающая среда, перемещается вверх, а воздух более холодный и более плотный – вниз. При слабом развитии конвекция имеет беспорядочный, турбулентный характер. При ее развитии над отдельными участками земной поверхности возникают восходящие и нисходящие токи воздуха (термики), иногда достигающие стратосферы. Вертикальная скорость восходящих токов при этом обычно порядка нескольких м/сек, но иногда может превышать 20 – 30 м/сек. С развитием конвекции связано образование кучевых и кучево-дождевых облаков и развитие гроз (об этом – ниже).
Ускорение конфекции а, т.е. вертикальное ускорение термиков, можно рассчитать из условия баланса сил: выталкивающей (архимедовой) силы, силы тяжести и силы инерции. Пусть элементарный объем 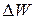 прогретого воздуха с температурой Тi и плотностью pi окружен более холодным атмосферным воздухом с температурой Т и плотностью p. Тогда по закону Архимеда выталкивающая сила равна pgΔW сила тяжести равна pigΔW, а сила инерции apigΔW, откуда следует уравнение равновесия
прогретого воздуха с температурой Тi и плотностью pi окружен более холодным атмосферным воздухом с температурой Т и плотностью p. Тогда по закону Архимеда выталкивающая сила равна pgΔW сила тяжести равна pigΔW, а сила инерции apigΔW, откуда следует уравнение равновесия
pgΔW – pigΔW = apiΔW.
Следовательно, ускорение конвекции равно 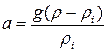 . Выразив плотность из уравнения состояния газа (1.1.), получим окончательно
. Выразив плотность из уравнения состояния газа (1.1.), получим окончательно
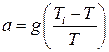 .
.
Таким образом, ускорение конвекции пропорционально разнице температуры 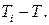
Конвекция, наряду с турбулентным перемешиванием, играет важную роль в процессе теплообмена земной поверхности с атмосферой.
Теплообмен земной поверхности с почвой (Р). Точно также за счет разницы температуры земной поверхности и нижележащих слоев почвы, земная поверхность может получать или терять тепло за счет механизма молекулярной теплопроводности. Если температура поверхности почвы выше, чем почвенно-грунтовой толщи, то теплопоток направлен вниз и считается отрицательным. В противном случае он направлен вверх и считается положительным. Суммарный теплопоток за год (при осреднении за многолетний период), очевидно, равен нулю.
С фазовыми превращениями воды связан другой механизм передачи тепла. Вода, как известно, может изменять свое агрегатное состояние (пар, жидкость, лед). Так, если земная поверхность испаряет воду, она теряет тепло на процесс испарения. Если, напротив, атмосферный пар конденсируется на земной поверхности, она получает тепло, выделяющееся при конденсации. Пусть Z – слой испарившейся или сконденсированной воды (мм). Тогда теплопоток за счет испарения или конденсации равен произведению (L∙Z), где L= 2.512 мДж/м2мм – удельная теплота испарения-конденсации.
Теплота (Т), выделяемая при замерзании воды, или затраченная на таяние снега и льда на земной поверхности, называется теплотой замерзания-таяния [46]. Как известно, удельная теплота плавления (таяния) равна 330 кДж/кг. Высокая удельная теплота плавления льда или снега (для сравнения – удельная теплоты плавления железа равна 270 кДж/кг) служит важным фактором в обороте тепла на Земле.
С учетом всех перечисленных выше потоков тепла, уравнение теплового баланса земной поверхности (3.1) получит следующий вид:
В+ А+Р+ LZ+Т=0. (3.2)
(напомним, потоки тепла, приходящие к поверхности, считаются положительными, а потоки, уходящие от неё, – отрицательными).
В засушливых районах, где выпадает мало осадков, потери тепла на испарение (LZ) сокращаются, тогда как затраты тепла на прогрев атмосферного воздуха и почвы возрастают (по сравнению с районами достаточного или избыточного увлажнения). Если же проводить оросительные мелиорации, то увеличатся затраты тепла на испарение. Согласно уравнению теплового баланса(1.13), при одинаковом радиационном балансе (В) снизится прогрев приземного воздуха и почвы (А+Р), что создаст более комфортный микро- или мезоклимат (предполагается, что затраты тепла на таяние снега (Т) практически не изменятся).
В зоне избыточного увлажнения (северная тайга, лесотундра, тундра) при осушении земель произойдет сокращение затрат тепла на испарение, а прогрев приземного воздуха и почвы (А+Р) соответственно возрастет. Значит, летние температуры воздуха и почвы повысятся, что опять-таки создаст более комфортный микро- или мезоклимат [17].
Таким образом, с помощью мелиорации возможно управлениемикро- и даже мезоклиматом.
Поскольку для годового периода теплопоток в почву равен нулю, формула (3.2) получит более простой вид:
В+ А+ LZ+Т=0. (3.3)
При возрастании увлажнения земной поверхности потери тепла не испарение (LZ) также возрастают. М.И. Будыко, пренебрегая величиной (А+Т) по сравнению с остальными величинами, записал:
В+ LZmax =0, (3.4)
где Zmax – максимально возможное испарение, которое соответствует условию, когда все тепло радиационного баланса полностью расходуется на процесс испарения. В алгебраической сумме (3.4) первый член входит со знаком «плюс», второй – со знаком «минус». Переходя к абсолютным величинам теплопотоков, М.И. Будыко на основе (3.4) предложил следующую широко известную формулу максимально возможного испарения:
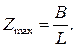 (3.5)
(3.5)
В конце 1950-х гг. в результате проведения работ Международного геофизического года в полярных странах (в высоких широтах) стало очевидным, что, годовой радиационный баланс (В) в полярных районах отрицательный, т.е. поступление солнечной радиации к земной меньше ее эффективного излучения. В этом случае формула (3.5) дает отрицательную величину максимально возможного испарения, что не имеет смысла. Выход из этой ситуации был предложен В.С. Мезенцевым [59].
Напомним (раздел 2.8), что разность между поглощенной радиацией (Isр) и эффективным излучением(Ее) называется радиационным балансом земной поверхности(В):
В=Isр– Ее.
Заметим, что поглощенная радиация солнца поступает только в дневное время, тогда как эффективное излучение происходит круглосуточно. Представив эффективное излучение в виде суммы дневного (ЕД) и ночного (ЕН), т.е. Ее=ЕД+ЕН и подставив ее в формулу для В, запишем
В=Isр– ЕД – ЕН, или
В= В+– ЕН,(3.6)
где В+= Isр– ЕД– дневной радиационный баланс (поглощенная радиация минус дневное эффективное излучение).
Обратимся к уравнению теплового баланса земной поверхности (3.2), в котором В.С. Мезенцев [59] учитывает также тепло конденсации водяных паров воздуха на земной поверхности (LС)
В+ А+Р+ LZ+ LС+Т=0, (3.7)
где С – слой сконденсированной влаги (мм), L – удельная теплота испарения-конденсации.
Представим, следуя Мезенцеву, составляющие потоков тепла в следующем виде:
А=А+ – А–,
 Р=Р+ – Р–, (3.8)
Р=Р+ – Р–, (3.8)
где А+ и А–, Р+ и Р–– значения по абсолютной величине положительных и отрицательных потоков тепла соответственно:
· между земной поверхностью и атмосферой (А+ передача тепла от более теплой атмосферы к более холодной земной поверхности; А–– то же самое от более теплой поверхности к более холодной атмосфере);
· между земной поверхностью и толщей почвогрунта (Р+ и Р–).
Напомним, что теплопоток положителен, если он направлен к земной поверхности, и отрицателен – если направлен от нее (рис. 3.1).
Количество переданного земной поверхности тепла в результате турбулентного теплообмена с атмосферой за счет переноса (адвекции) теплых воздушных масс – есть адвективное тепло А+.
Система теплопотоков в (3.7) записана в виде алгебраической суммы. Перепишем это уравнение с учетом выражений (3.6) и (3.8), оставив в левой части положительные составляющие потоков тепла, а в правой – отрицательные, и представив их по абсолютной величине
(В++ А++ Р+) – Т = LZ+ (ЕН – LС) + А–+ Р–. (3.9)
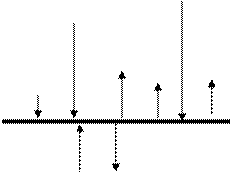 В+
В+
А+
LС А–
Т– 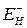
Р+ Р–
Рис. 3.1. Схема теплообмена на земной поверхности
В (3.9) В.С. Мезенцев теплоту конденсации (LС) оставляет в правой части, поскольку конденсация синхронизируется по времени с ночным эффективным излучением (ЕН). Далее учтем, что затраты тепла на таяние сезонного снега и почвенного льда (Т) осуществляются в период снеготаяния, за счет положительных теплопотоков этого периода. Поэтому эти затраты оставлены в правой части (3.9).
В средних широтах за теплое время года почва получает тепла (Р+) от 1.5 до 3.0 ккал/см2. В холодное время года почва, остывая, это же количество тепла (Р–) отдает атмосфере. Величина ±1.5÷3.0 ккал/см2 (±280÷640 МДж/м2) представляет годовой теплооборот почвы. Очевидно, для годового периода Р+= Р–. С учетом этих замечаний уравнение теплового баланса (3.9) для годового периода получает вид
(В++ А+) – Т = LZ+ (ЕН – LС) + А–. (3.10)
Из (3.10) запишем выражение для потерь тепла на испарение
LZ = (В++ А+– Т) – [(ЕН– LС) + А–]. (3.11)
Если увеличивать увлажнение деятельной поверхности, то из-за возрастания испарения (Z) начнут возрастать и потери тепла на испарение (LZ), а отдача тепла на согревание приземного воздуха (А–) начнет сокращаться. При этом в ночные часы возрастет выделение тепла конденсации (LС), следовательно, разница (ЕН– LС) соответственно уменьшится. Таким образом, с увеличением испарениявеличина [(ЕН– LС) + А–] в (3.10) также начнет уменьшаться.В пределе, если все тепло (В++ А+– Т) окажется израсходованнымна процесс испарения, можно записать
LZmax = (В++ А+– Т), (3.12)
откуда
Zmax = 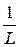 (В++ А+– Т), (3.13)
(В++ А+– Т), (3.13)
где Zmax – максимально возможное испарение за годовой период в трактовке В.С. Мезенцева и его школы [59].
Введем обозначения:
Тк = В++ А+ , (3.14)
Tzmax = В++ А+– Т, (3.15)
где Тк – годовые теплоэнергетические ресурсы (ТЭР) климата, 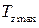 – годовые теплоэнергетические ресурсы (ТЭР) максимально возможного испарения.
– годовые теплоэнергетические ресурсы (ТЭР) максимально возможного испарения.
Таблица 3.1
Теплоэнергетические ресурсы климата за год Тк, дневной (положительный) радиационный баланс (В+), положительная составляющая турбулентного теплообмена с атмосферой (А+) и годовой радиационный баланс (В), МДж/(м2·год) [47]
| Станция | Тк | В+ | А+ | В |
| Антарктида | ||||
| Восток Мирный | –126 –197 | |||
| Арктика | ||||
| Купол Чюрлёниса Барьер Сомнений Мыс Желания | –73 –115 | |||
| Сибирь | ||||
| Мыс Челюскин Тикси Салехард Тура Якутск Омск | ||||
| Казахстан | ||||
| Астана Джезказган |
В табл. 3.1 для некоторых станций Арктики, Антарктиды, Сибири и Центральной Азии приведены значения ТЭР климата Тк, значения В+ и А+. Для сравнения в последнем столбце даны значения годового радиационного баланса В= В+– ЕН. Анализ второго и пятого столбцов табл. 3.1 показывает, что годовой радиационный баланс В на севере Сибири и в полярных областях планеты утрачивает энергетическую информативность – годовые суммы получаются нулевыми и отрицательными.
Представленный анализ структуры теплового баланса уточнил представления об энергетической основе физико-географического процесса. Он показал, что важное энергетическое значение в Антарктиде, Арктике и на Севере Сибири имеет адвективное тепло, поступающее из экваториальных, субэкваториальных и умеренных широт (третий столбец табл. 3.1).
Дата добавления: 2015-09-07; просмотров: 3226;
