Для перехода от величины давления, выраженной в миллиметрах ртутного столба, к величине в миллибарах нужно ввести сомножитель 4/3; для обратного перехода – 3/4.

Рис. 1.2. Барометр-анероид М-110. Предназначен для измерения атмосферного давления воздуха. Диапазон измеряемого давления от 5 до 790 мм.рт.ст. Габаритные размеры: диаметр – 205 мм, высота – 125 мм
Плотность сухого воздуха определяется из уравнения состояния газа Менделеева-Клапейрона, рассматриваемого в курсе физики:
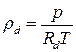 , (1.1)
, (1.1)
где 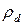 – плотность сухого воздуха (кг/м3), p – давление (Па), Т – абсолютная температура (К), Rd – удельная газовая постоянная сухого воздуха, равная 287 м2/(с2К).
– плотность сухого воздуха (кг/м3), p – давление (Па), Т – абсолютная температура (К), Rd – удельная газовая постоянная сухого воздуха, равная 287 м2/(с2К).
Плотность влажного воздуха определяется по формуле, которая выводится из рассмотрения уравнений состояния газа, записанных раздельно для сухого воздуха и водяного пара:
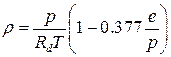 , (1.2)
, (1.2)
где е – парциальное давление водяного пара.
Последнее уравнение можно привести к виду
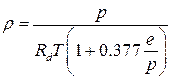 . (1.3)
. (1.3)
Выражение в знаменателе (1.3) 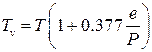 принято называть виртуальной температурой. Тогда (1.3) получает вид уравнения (1.1), в котором истинная температура заменяется виртуальной, т.е.
принято называть виртуальной температурой. Тогда (1.3) получает вид уравнения (1.1), в котором истинная температура заменяется виртуальной, т.е.
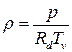 . (1.4)
. (1.4)
Из (1.3) видно, что плотность влажного воздуха несколько ниже, чем сухого, поскольку водяной пар менее плотен, чем сухой воздух. При нормальном давлении и температуре воздуха 0о разница плотностей сухого и влажного воздуха составляет менее 0.25 %.
Плотность сухого воздуха ρd при температуре 0° и давлении 1000 гПа равна 1276 г/м3, а при давлении 1013 гПа – 1293 г/м3. С удалением от земной поверхности плотность атмосферного воздуха снижается. Так если у поверхности земли плотность сухого воздуха составляет в среднем 1293 г/м3, на высоте 100 км плотность менее 0,001 г/м3, на отметке 750 км – 10-10 г/м3, а на высоте нескольких тысяч километров она ничтожно мала: атмосфера постепенно переходит в космическое пространство.
Барометрическая формула. Закон, по которому изменяется атмосферное давление с высотой, описывает барометрическая формула, или формула экспоненциальной атмосферы, известная со времен Лапласа (1749 – 1827).
Рассмотрим вертикальный столб воздуха с поперечным сечением, равным единице (рис.1.3). Силы, действующие на этот объем, направленные вниз, запишем со знаком минус, а направленные вверх – со знаком плюс.
Выделим в нем бесконечно тонкий слой толщиной dz, ограниченный снизу поверхностью на высоте z, и сверху – на высоте z + dz.
На нижнюю поверхность элементарного объема окружающий воздух давит снизу вверх с силой давления р (Па). На верхнюю поверхность смежный воздух действует с силой давления – (p + dp), направленной сверху вниз, где dp – изменение силы атмосферного давления при изменении высоты на dz.
Полагаем, что в горизонтальном направлении атмосферное давление не меняется, т.е. силы давления, действующие на боковые стенки, уравновешиваются и их равнодействующая равна нулю.
Воздух в рассматриваемом элементарном объеме создает силу тяжести –gdm направленную вниз (g – ускорение свободно падающего тела, dm – масса воздуха во взятом элементарном объеме). Так как площадь поперечного сечения, равна единице, то объем равен dz, а масса воздуха в нем равна ρdz (ρ – плотность воздуха). Следовательно, сила тяжести (–gdm) равна –ρgdz.
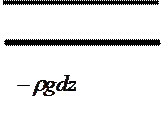
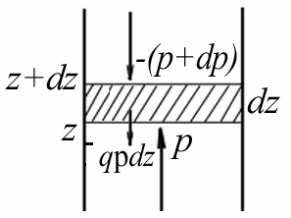
Рис. 1.3. Силы, действующие на элементарный объем воздуха
В неподвижной в атмосфере сила тяжести (вес) и силы давления уравновешиваются. Сумму всех этих трех сил приравняем нулю
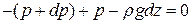 , (1.5)
, (1.5)
откуда следует
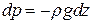 . (1.6)
. (1.6)
Таким образом, с высотой атмосферное давление падает, причем разность давлений на нижнем и верхнем уровнях рассматриваемого элементарного объема равна весу воздуха в этом объеме.
Дифференциальное уравнение (1.6) носит название основного уравнения статики атмосферы. Разделив его обе части на массу элементарного объема ρdz, основное уравнение статики можно написать еще так:
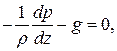 (1.7)
(1.7)
или
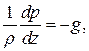 (1.8)
(1.8)
Величина –dp/dz есть вертикальный барический градиент (вертикальный градиент давления). Он характеризует изменение силы давления при подъеме на единицу высоты. Знак минус означает, что давление уменьшается с увеличением высоты.
Так как 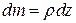 есть масса рассматриваемого элементарного объема, то уравнение (1.8) может быть записано в виде
есть масса рассматриваемого элементарного объема, то уравнение (1.8) может быть записано в виде
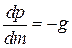 . (1.9)
. (1.9)
Поскольку dp равно изменению атмосферного давления при изменении высоты на dz, то из (1.9) следует, что отношение силы dp к массе элементарного объема dm равно ускорению силы тяжести –g, направленному вниз. Из (1.9) следует также, что
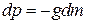 . (1.10)
. (1.10)
Иными словами, природа силы 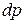 – сила тяжести рассматриваемой элементарной массы воздуха dm (формула 1.10 выражает закон тяготения, изученный Галилеем, и обобщенный как закон всемирного тяготения Ньютоном).
– сила тяжести рассматриваемой элементарной массы воздуха dm (формула 1.10 выражает закон тяготения, изученный Галилеем, и обобщенный как закон всемирного тяготения Ньютоном).
Проинтегрируем уравнение (1.6) в пределах от уровня z1 с давлением р1 до вышележащего уровня z2 с давлением р2. При этом необходимо учесть, что плотность воздуха (ρ) изменяется с высотой.. Представим плотность воздуха через температуру и давление с помощью уравнения состояния газов (1.1) ρ = p/RT. Подставив это значение в уравнение (1.6), получим

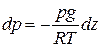 (1.11)
(1.11)
или
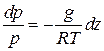 (1.12)
(1.12)
Интегрируем обе части уравнения (1.12) в пределах от р1 до р2 и от z1 до z2, и выносим постоянные g и R за знак интеграла:
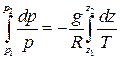
или
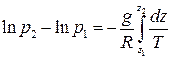 (1.13)
(1.13)
Температура Т изменяется по высоте, причем эта функция не может быть точно выражена математически. По этой причине исходим из среднего значения температуры Тm между уровнями z1 и z2. Определить Тm можно с достаточным приближением, зная температуру на уровнях z1 и z2 и взяв среднее арифметическое. Итак, заменяя переменную Т постоянной величиной Тm , вынося ее за знак интеграла, интегрируя правую часть (1.13) и преобразуя левую, получим
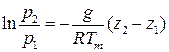 (1.14)
(1.14)
Потенцируя (1.14), получим:
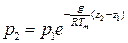 (1.15)
(1.15)
Уравнение (1.14) или (1.15) представляют собой различную запись интеграла основного уравнения статики атмосферы, или барометрической формулы, которая показывает, как меняется атмосферное давление в зависимости от высоты и температуры воздуха.
Выше было показано, что бесконечно малая разность давлений на уровнях 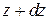 и
и 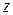 равна весу элементарного объема воздуха сечением единица и толщиной dz. Отсюда понятно, что и разность давлений между нижним z1 и верхним уровнем z2 равна весу воздушного столба между ними.
равна весу элементарного объема воздуха сечением единица и толщиной dz. Отсюда понятно, что и разность давлений между нижним z1 и верхним уровнем z2 равна весу воздушного столба между ними.
С помощью барометрической формулы можно решить следующие задачи:
1) зная давление на одном уровне и среднюю температуру слоя воздуха, найти давление на другом уровне;
2) барометрическое нивелирование – зная давление на обоих уровнях и среднюю температуру слоя воздуха, найти разность уровней (ошибка этого метода до высоты 2000 м составляет не более 1 м);
3) зная разность уровней и величины давления на них, найти среднюю температуру столба воздуха.
Важным вариантом первой задачи, является приведение давления к уровню моря. Зная давление и температуру на некоторой высоте z над уровнем моря, вычисляют среднюю температуру в слое z, используя средний вертикальный градиент температуры. В тропосфере он принимается равным 0,6° на 100 м. После этого по давлению на высоте z и по полученной средней температуре определяется давление на уровне моря. В случае влажного воздуха в расчетах берется значение Rd для сухого воздуха, умноженное на (1+0,377e/p). Иначе говоря, берется Rd для сухого воздуха, но температура заменяется виртуальной температурой (см. выше). Кроме того, используется соотношение для ускорения силы тяжести g, в зависимости от географической широты и высоты над уровнем моря [12].
Подчеркнем, что на приземные синоптические карты всегда наносится давление, приведенное к уровню моря, чем исключается влияние различий в высотах станций на величины давления.
Барическая ступень. Запишем основное уравнение статики в виде:
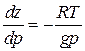 . (1.16)
. (1.16)
Величина dz/dp называется барической ступенью. Барическая ступень – величина, обратная вертикальному барическому градиенту –dp/dz, означающая превышение по высоте, при котором атмосферное давление падает на единицу. Из формулы (1.16) следует, что барическая ступень обратно пропорциональна величине давления и прямо пропорциональна абсолютной температуре воздуха. Чем больше высота (и чем, следовательно, ниже давление), тем больше барическая ступень. Элементарные расчеты по (1.16) показывают, что при температуре 0° и давлении 1000 гПа (напомним, 1 гПа=100 Па) барическая ступень равна 8 м/гПа. Следовательно, при давлении 1000 гПа у земной поверхности нужно подняться на 8 м, чтобы давление упало на 1 гПа. Другой пример [85]: на высоте около 5 км, где давление близко к 500 гПа, барическая ступень при температуре воздуха 0оС (273оК), равна 16 м/гПа. С изменением температуры барическая ступень растет на 0.4 % на каждый градус.
Подобные расчеты для не очень больших высот позволяют приводить давление воздуха к уровню моря.
Если в теплом и в холодном воздухе давление внизу одинаково, то в теплом воздухе, где барическая ступень больше, давление падает с высотой медленнее, чем в холодном. Поэтому на одинаковых высотах в теплом воздухе давление будет выше, чем в холодном. Отсюда следует важный вывод: теплые области в атмосфере являются в высоких слоях атмосферы областями высокого давления, а холодные области – областями низкого давления.
Распределение атмосферного давления по высоте, как это следует из выше изложенного, зависит от давления у поверхности и от распределения температуры воздуха с высотой. Для Европы давление на уровне моря в среднем равно 1014 гПа, на высоте 5 км – 538 гПа, 10 км – 262 гПа, 15 км – 120 гПа и 20 км – 56 гПа, т.е. убывает примерно в геометрической прогрессии, когда высота возрастает в арифметической прогрессии. Действительно, на уровне 5 км давление почти вдвое ниже, чем на уровне моря, на уровне 10 км – почти в четыре раза, на уровне 15 км – почти в 8 раз и на уровне 20 км – в 18 раз. Инструментальные наблюдения показывают, что давление меняется не только с высотой, но и в горизонтальной плоскости, а также непрерывно изменяется во времени.
Изменения давления во времени. Атмосферное давление в каждой точке атмосферы непрерывно изменяется. Изменения давления в основном носят непериодическийхарактер. Амплитуда колебаний среднесуточного давления увеличивается от экватора к умеренным и высоким широтам. Суточный ход давления ярче выражен в тропических широтах. В суточном ходе максимальные значения наблюдаются дважды в сутки – около 9 – 10 и 21– 22 часов по местному времени, а минимальные – около 3 – 4 и 15 – 16 часов (рис. 1.4).
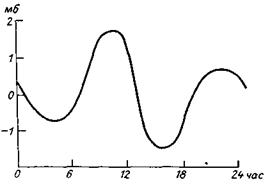
Рис. 1.4. Средний суточный ход атмосферного давления в Индийском океане [85].
При метеорологических наблюдениях вычисляют барическую тенденцию – величину изменения давления за последние 3 часа перед сроком наблюдений. От тропиков к полюсам амплитуда суточных колебаний убывает от 2 – 4 гПа до десятых долей миллибара, в средних и полярных широтах более значительны непериодические колебания давления.
Причины суточного хода давления связаны с суточным ходом температуры воздуха, собственными упругими колебания атмосферы, возбуждаемыми колебаниями температуры; влияют также приливные волны в атмосфере.
Междусуточная изменчивость давления – это средняя многолетняя величина изменения давления за сутки. У земной поверхности в умеренных широтах средняя междусуточная изменчивость давления в средних и высоких широтах составляет 3 – 10 гПа. Она увеличивается при усилении циклонической деятельности, обычно зимой. В тропиках междусуточная изменчивость давления составляет десятые доли миллибара, что значительно меньше амплитуды суточного хода. Междусуточная изменчивость давления в умеренных широтах значительна во всей толще тропосферы. В течение года в среднем колебания давления в умеренных широтах достигают 50 – 80 гПа,под экватором примерно 10 – 15 гПа.
В Барнауле в январе 1900 г. наблюдалось давление, которое после приведения к уровню моря оказалось равным 1080 гПа, а в центре тайфуна над Японией в сентябре 1934 г. было отмечено давление на уровне моря. 884 гПа [85], разница составляет 196 гПа.
Дата добавления: 2015-09-07; просмотров: 1724;
