Лавинное разрушение сжатых стержней
Образование лавинного или прогрессирующего разрушения может произойти на нижних этажах высотных зданий во время землетрясения или по причине перегрузки из за ошибки при проектировании. В любом случае расчёт на такое разрушение должен быть выполнен заранее на стадии проектирования. Расчёт на устойчивость высотных зданий был исследован во многих работах и в частности в работе [1]. Критерий возникновения лавинного разрушения для растянутых стержней (канатов) был предложен в предыдущей работе автора [2], однако для сжатых стержней, как будет показано ниже, такой критерий имеет совершенно иной вид.
В качестве примера рассмотрен нижний этаж высотного здания с металлическим каркасом из 25 колонн, высота этажа принята H=3.5м , сечение колонн принято двутавровым 40К5 из стали марки С345 с расчётным сопротивлением 30кг/мм2. В качестве разбега предела текучести принят коэффициент 1,5. Таким образом, значение расчётного сопротивления, которому соответствует вероятность Р=0 (i=0) принято Rmin= R0=30кг/мм2 , а максимальное значение предела текучести принято Rmаx= 45кг/мм2 , вероятность которого равна Р=1 (i=26). Ниже для описания пластических свойств материала принята идеально пластическая диаграмма Прандтля.
Учитывая ограниченность вероятностного распределения, в качестве аппроксимирующей функции также как в работе [1] принята полуволна синусоиды (рис.1)
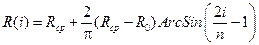
 (1)
(1)
со средним значением Rср=(R0+Rmax)/2=37.5кг/мм2 при вероятности Р=0.5.
Номера колонн i, вероятности пределов текучести P(i), расчётные сопротивления R(i), а также деформации текучести или, что тоже самое, безразмерные горизонтальные перемещения правого конца по схеме рис.3, приведены в Таблице 1.
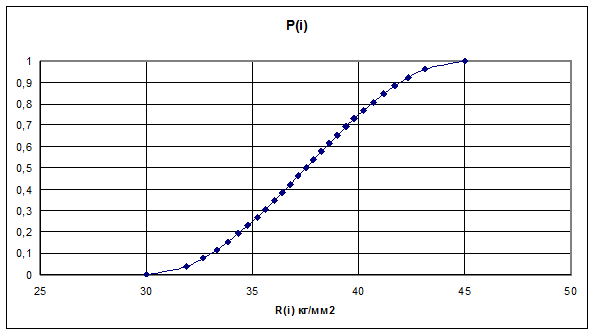
Рис. 1. Аппроксимация вероятностного распределения предела текучести
Если рассмотреть кривые отпорности в безразмерном виде 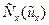 , где
, где 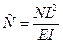 ,
, 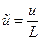 , показанные на рис.2 и рассчитанные в соответствии с методом книги [3] по схеме показанной на рис.3 для значений
, показанные на рис.2 и рассчитанные в соответствии с методом книги [3] по схеме показанной на рис.3 для значений 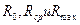 , то легко заметить, что в безразмерном
, то легко заметить, что в безразмерном
Таблица 1
| i | |||||||||
| Р(i) | 0,038462 | 0,076923 | 0,115385 | 0,153846 | 0,192308 | 0,230769 | 0,269231 | 0,307692 | |
| Ri(i) | 31,88499 | 32,68369 | 33,30959 | 33,84891 | 34,33501 | 34,78509 | 35,20946 | 35,61501 | |
| ux(i) | 0,001429 | 0,001518 | 0,001556 | 0,001586 | 0,001612 | 0,001635 | 0,001656 | 0,001677 | 0,001696 |
| 0,346154 | 0,384615 | 0,423077 | 0,461538 | 0,5 | 0,538462 | 0,576923 | 0,615385 | 0,653846 | |
| 36,00665 | 36,38814 | 36,76251 | 37,13236 | 37,5 | 37,86764 | 38,23749 | 38,61186 | 38,99335 | |
| 0,001715 | 0,001733 | 0,001751 | 0,001768 | 0,001786 | 0,001803 | 0,001821 | 0,001839 | 0,001857 | |
| 0,692308 | 0,730769 | 0,769231 | 0,807692 | 0,846154 | 0,884615 | 0,923077 | 0,961538 | ||
| 39,38499 | 39,79054 | 40,21491 | 40,66499 | 41,15109 | 41,69041 | 42,31631 | 43,11501 | ||
| 0,001875 | 0,001895 | 0,001915 | 0,001936 | 0,00196 | 0,001985 | 0,002015 | 0,002053 | 0,002143 |
виде начальные участки до максимума имеют одинаковые безразмерные модули 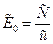 , а в закритической области, после достижения критического состояния, кривые также можно аппроксимировать прямыми с отрицательными наклонами, характеризуемыми безразмерными отрицательными модулями
, а в закритической области, после достижения критического состояния, кривые также можно аппроксимировать прямыми с отрицательными наклонами, характеризуемыми безразмерными отрицательными модулями 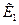 , зависящими от расчётного сопротивления колонны, то есть от номера i.
, зависящими от расчётного сопротивления колонны, то есть от номера i.
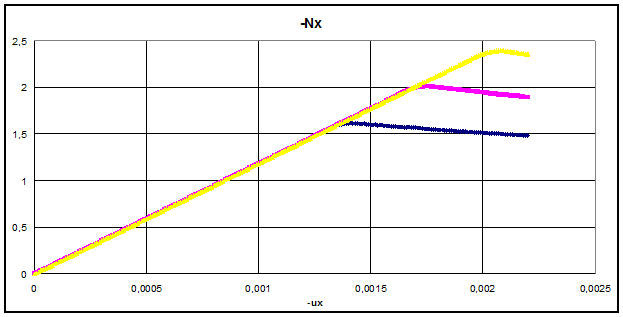
Рис. 2. Кривые отпорности для значений R0, Rcp и Rmax
Именно наличие участков с отрицательными наклонами в закритической области затрудняет и расчёты и само возникновение лавинного разрушения.
Для описания процесса деформирования вначале полезно рассмотреть безразмерные модули на стадии роста усилий и в закритической области. В первом приближении эти модули определяются следующими формулами:
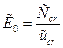 (2)
(2) 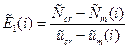 (
(  ) (3)
) (3)
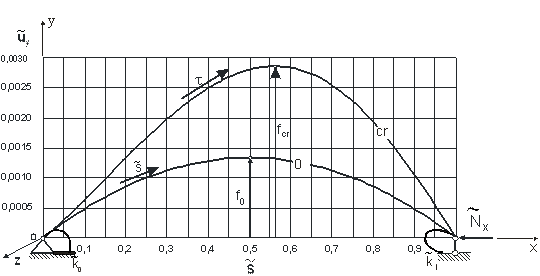
Рис. 3. Начальная погибь и критический прогиб, к0=1000 (заделка), к1=0 (шарнир)
где индекс "сr" показывает, что величина относится к максимальным точкам на кривых отпорности рис. 2, а индекс "m" стоит у величин с максимальными значениями перемещений 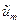 =0.0022. Шаг деформирования при вычислениях был принят следующим
=0.0022. Шаг деформирования при вычислениях был принят следующим 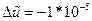 .
.
Неточность формул (2) и (3) связана с тем, что вершины кривых отпорности рис. 2 имеют плавное скругление показанное на рис. 4 для Rmax . Для определения модуля 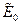 целесообразно выбрать точку вне закругления и получить практически точное значение
целесообразно выбрать точку вне закругления и получить практически точное значение 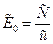 =1183 для всех колонн (любое i). При определении модуля
=1183 для всех колонн (любое i). При определении модуля 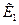 проще всего использовать формулу (3), отступив от максимального значения на десять шагов деформирования в большую сторону для всех i. Для расчётных сопротивлений
проще всего использовать формулу (3), отступив от максимального значения на десять шагов деформирования в большую сторону для всех i. Для расчётных сопротивлений 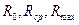 вычисленные таким образом модули
вычисленные таким образом модули 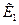 имеют следующие значения -191,8 ; -270,9 ; -384,5, которые оказались значительно меньшими по абсолютной величине модуля
имеют следующие значения -191,8 ; -270,9 ; -384,5, которые оказались значительно меньшими по абсолютной величине модуля 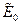 .
.
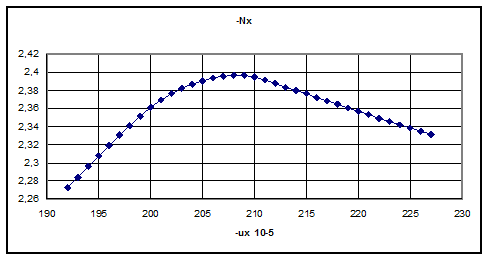
Рис. 4. Вершина кривой отпорности для Rmax
В качестве аргумента процесса нагружения целесообразно использовать деформации ux, а не нагрузки, так как последние проходят через максимум. При этом приходится решать обратную задачу, определяя нагрузки в зависимости от деформаций. Учитывая, что вначале все колонны имеют одинаковые модули упругости, в начале нагружения в них возникают одинаковые усилия и можно подсчитать суммарную нагрузку Nn=Ni n, где n=25-число колонн в сооружении. Однако в качестве критериальной функции удобнее использовать среднее усилие Nc или среднее напряжение Sc в колоннах в размерном или в безразмерном виде.
После того как слабейшая колонна потеряет устойчивость, а деформации продолжат увеличиваться, во всех не потерявших устойчивость колоннах усилия будут увеличиваться, в то время как в колоннах потерявших устойчивость усилия будут уменьшаться, так что суммарное усилие, а следовательно и среднее усилие Nc, может как расти, так и уменьшаться. С увеличением числа колонн потерявших устойчивость и уменьшением числа колонн не потерявших устойчивость суммарное усилие будет расти медленнее, а суммарное усилие в потерявших устойчивость колоннах будет уменьшаться быстрее и наступит такой момент, когда рост суммарного усилия в колоннах не потерявших устойчивости сравняется с суммарным уменьшением усилий в колоннах потерявших устойчивость. Дальнейший рост деформаций уже не будет нуждаться в увеличении внешних нагрузок, начнётся лавинное разрушение всей конструкции. Поэтому в качестве критерия начала лавинного разрушения следует принять условие достижения величиной Nc максимального значения:
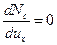 (4)
(4)
Отрицательные модули закритического уменьшения усилий ограничены двумя крайними значениями: 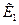 =-
=-  и
и 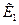 =0, для которых средние напряжения по всем колоннам определяются двумя простыми формулами:
=0, для которых средние напряжения по всем колоннам определяются двумя простыми формулами:
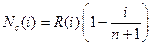
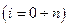 для
для 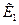 =-
=-  (5)
(5)
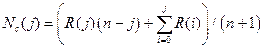
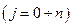 для
для 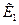 =0 (6)
=0 (6)
Первый случай можно назвать "хрупким" разрушением колонн, так как после потери устойчивости колонна перестаёт нести какую-либо нагрузку. Второй случай скорее близок к "идеально пластическому типу", так как колонна после потери устойчивости продолжает деформироваться, неся критическую нагрузку.
Зависимость 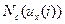 для хрупкого разрушения показана на Рис.5, откуда видно, что лавинное разрушение начинается после потери устойчивости самой слабой (i=1) из 25 колонн.
для хрупкого разрушения показана на Рис.5, откуда видно, что лавинное разрушение начинается после потери устойчивости самой слабой (i=1) из 25 колонн. 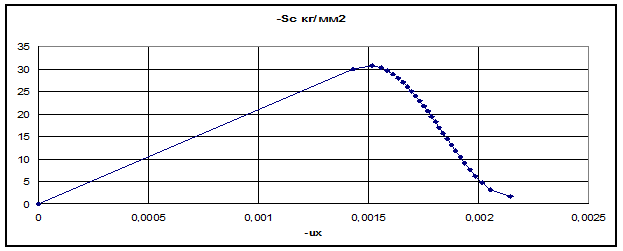
Рис. 5. Зависимость 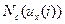 для "хрупкого" разрушения.
для "хрупкого" разрушения.
Крайние точки на этом графике не следует принимать во внимание, так как они относятся к значениям R0 и Rmаx , имеющим вероятности P=0 и P=1.
Аналогичная зависимость для разрушения идеально пластического типа показана на Рис. 6, из которого видно, что лавинного разрушения не происходит вовсе, и конструкция разрушается только после потери устойчивости самой прочной колонны (i=25).
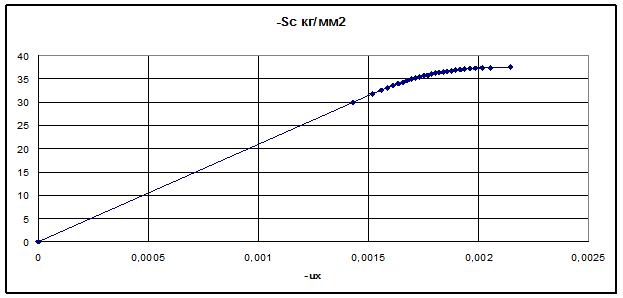
Рис. 6. Зависимость 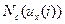 для "идеально пластического" разрушения.
для "идеально пластического" разрушения.
Для расчёта критерия лавинного разрушения с учётом реального закритического поведения колонн необходимо произвести расчёт кривых отпорности для всех колонн, для чего составляется полная таблица, приведенная в сокращённом в настоящей статье.
Вывод всех данных в таблице производится с интервалом в десять шагов деформирования 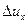 =0.0001 . Кривые отпорности приведены только для трёх колонн под номерами 1, 13 и 25 в безразмерном виде: Nx с указанием расчётных сопротивлений R(i) этих колонн. Величина среднего напряжения в колонне Sc для наглядности приведена в размерном виде и определена по полному списку колонн.
=0.0001 . Кривые отпорности приведены только для трёх колонн под номерами 1, 13 и 25 в безразмерном виде: Nx с указанием расчётных сопротивлений R(i) этих колонн. Величина среднего напряжения в колонне Sc для наглядности приведена в размерном виде и определена по полному списку колонн.
По данным приведенным в таблице построен график кривой отпорности для среднего напряжения, показанный на Рис.7.
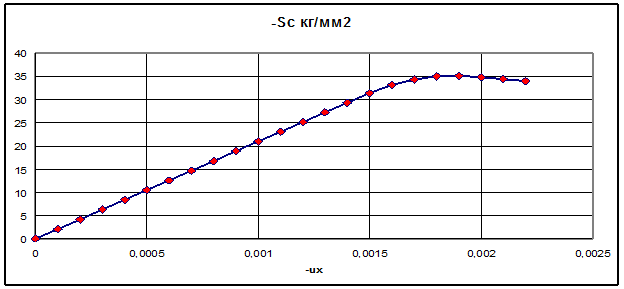
Рис.7. Критериальная кривая отпорности
Сокращённая Таблица 2 расчёта кривых отпорности
и среднего напряжения Sc в колоннах
| i | ||||
| R(i)кг/мм2 | 31,88 | 37,5 | 43,12 | |
| -ux | -Sc кг/мм2 | -Nx | -Nx | -Nx |
| 0,0001 | 2,09708882 | 0,118413 | 0,118413 | 0,118413 |
| 0,0002 | 4,19408978 | 0,23682 | 0,23682 | 0,23682 |
| 0,0003 | 6,29099851 | 0,355223 | 0,355223 | 0,355223 |
| 0,0004 | 8,38781034 | 0,47362 | 0,47362 | 0,47362 |
| 0,0005 | 10,4845203 | 0,592011 | 0,592011 | 0,592011 |
| 0,0006 | 12,5811232 | 0,710397 | 0,710397 | 0,710397 |
| 0,0007 | 14,6776133 | 0,828775 | 0,828775 | 0,828775 |
| 0,0008 | 16,7739847 | 0,947148 | 0,947148 | 0,947148 |
| 0,0009 | 18,8702309 | 1,065513 | 1,065513 | 1,065513 |
| 0,001 | 20,9663452 | 1,18387 | 1,18387 | 1,18387 |
| 0,0011 | 23,0623202 | 1,30222 | 1,30222 | 1,30222 |
| 0,0012 | 25,1581481 | 1,420562 | 1,420562 | 1,420562 |
| 0,0013 | 27,2538206 | 1,538894 | 1,538894 | 1,538894 |
| 0,0014 | 29,3491031 | 1,656887 | 1,657218 | 1,657218 |
| 0,0015 | 31,382567 | 1,716791 | 1,775531 | 1,775531 |
| 0,0016 | 33,1067576 | 1,696348 | 1,893835 | 1,893835 |
| 0,0017 | 34,3279315 | 1,67536 | 1,995814 | 2,012127 |
| 0,0018 | 34,9649694 | 1,655352 | 1,998748 | 2,130407 |
| 0,0019 | 35,0658342 | 1,636379 | 1,971169 | 2,246565 |
| 0,002 | 34,8065953 | 1,618376 | 1,944789 | 2,300354 |
| 0,0021 | 34,4005101 | 1,601259 | 1,920019 | 2,268688 |
| 0,0022 | 33,9685536 | 1,584947 | 1,89675 | 2,234383 |
По Таблице 2 можно определить значение ux=0.00190, соответствующее максимальному значению Sc=35,06 кг/мм2, а затем по Таблице1 определить номер колонны i=19, с которой началось лавинное разрушение. При этом максимальное усилие в колонне Nc=Sc*A=1300,7т, где А=371см2 -площадь поперечного сечения колонны.
Приведенный пример и сама методика расчёта наступления лавинного разрушения основана на принятых гипотезах, которые безусловно нуждаются в проверках и уточнениях. Например гипотеза об идеальной пластичности с использованием диаграммы Прандтля может быть заменена на унифицированную диаграмму строительных сталей [4]. Проведенные расчёты по предлагаемой методике с использованием унифицированной диаграммы показали, что результаты этих двух расчётов заметно отличаются друг от друга. Так безразмерные модули Е0 в обоих расчётах практически совпали, так как они относятся к упругому деформированию, однако безразмерные модули Е1 , относящиеся к закритическому деформированию, оказались немного разными: для кривых отпорности  их значения оказались равными: -88,95; -129,4; -172,5, то есть значительно меньшими приведенных выше. Критериальная кривая отпорности также оказалась немного отличной от приведенной на рис.7 и номер колонны, при потере устойчивости которой начинается лавинное разрушения оказался i=23.
их значения оказались равными: -88,95; -129,4; -172,5, то есть значительно меньшими приведенных выше. Критериальная кривая отпорности также оказалась немного отличной от приведенной на рис.7 и номер колонны, при потере устойчивости которой начинается лавинное разрушения оказался i=23.
Принятая величина разбега расчётных сопротивлений также нуждается в проверке, как и характер аппроксимации статистической кривой принятой в настоящей работе.
И наконец, характер перераспределения усилий также нуждается в уточнении. В работе этот вопрос не оговорён, и фактически делается предположение о том, что уменьшение усилий в потерявшей устойчивость колонне равномерно компенсируется увеличением усилий во всех не потерявших устойчивость колоннах.
| <== предыдущая лекция | | | следующая лекция ==> |
| уравнением моментов | | | Конъюнктивные и дизъюнктивные нормальные формы |
Дата добавления: 2015-09-28; просмотров: 796;
