Конъюнктивные и дизъюнктивные нормальные формы

(КНФ и ДНФ)

Элементарной дизъюнкцией называется дизъюнкция переменных высказываний и (или) их отрицаний.

Например: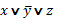

Элементарной конъюнкцией называется конъюнкция переменных высказываний и (или) их отрицаний.

Например: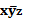

Конъюнктивной нормальной формой (КНФ) данной формулы называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.

Например, выражение 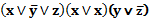– КНФ.

Дизъюнктивной нормальной формой (ДНФ) данной формулы называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.

Например, выражение 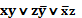является ДНФ.

Для того чтобы построить по данной формуле логики высказываний эквивалентную ей ДНФ или КНФ необходимо:

1. Выразить все операции через дизъюнкцию, конъюнкцию и отрицание;

2. Применять, пока возможно, законы де Моргана для того, чтобы отрицания стояли лишь над элементарными переменными высказываниями;

3. А) (для построения ДНФ). Применять, пока возможно, закон дистрибутивности конъюнкции относительно дизъюнкции для того, чтобы ни одна дизъюнкция не находилась в области действия конъюнкции;

Б) (для построения КНФ). Применять, пока возможно, закон дистрибутивности дизъюнкции относительно конъюнкции для того, чтобы ни одна конъюнкция не находилась в области действия дизъюнкции;

4. Применять (на каждом этапе) упрощающие эквивалентности.