Знакомство с расчетом токов напряжений и мощности MathCAD в цепях с синусоидальным и несинусоидальным периодическим током.
Любая синусоидальная функция может быть представлена в виде 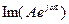 где A – комплексная амплитуда. Для расчета токов и напряжений цепи при синусоидальном токе используют комплексные амплитуды. Расчет цепи становится аналогичным расчету цепи с постоянным током, только реактивное сопротивление емкости и индуктивности полагают равными
где A – комплексная амплитуда. Для расчета токов и напряжений цепи при синусоидальном токе используют комплексные амплитуды. Расчет цепи становится аналогичным расчету цепи с постоянным током, только реактивное сопротивление емкости и индуктивности полагают равными 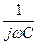 и
и 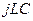 соответственно. При расчете цепи с периодическим несинусоидальным током токи и напряжения разлагаются в ряды Фурье и происходит расчет комплексных амплитуд для каждой гармонической составляющей. В приведенном ниже примере мы ограничимся расчетом периодического тока, так как синусоидальный ток представляет собой простейший частный случай периодического.
соответственно. При расчете цепи с периодическим несинусоидальным током токи и напряжения разлагаются в ряды Фурье и происходит расчет комплексных амплитуд для каждой гармонической составляющей. В приведенном ниже примере мы ограничимся расчетом периодического тока, так как синусоидальный ток представляет собой простейший частный случай периодического.
1.1. Рассмотрим пример:
 |
Дана следующая электрическая цепь
Напряжение источника питания периодично и разлагается на четыре гармонические составляющие. Требуется рассчитать ток, проходящий через индуктивность и напряжение на сопротивлении 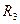 , a также потребляемую цепью мощность.
, a также потребляемую цепью мощность.
Расчет цепи произведем методом контурных токов, которые изображены на рисунке. Введем обозначения 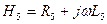 и
и 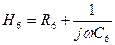
Тогда уравнения контурных токов имеют вид:
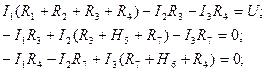
Или в векторно-матричном виде:
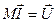
где 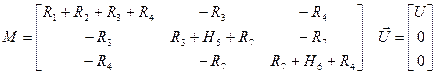
Очевидно, что решение этого уравнения имеет вид
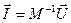
Данное уравнение надо решить для каждой гармонической составляющей. Осуществим это для каждой гармонической составляющей при помощи MathCAD. В результате имеем следующий код на MathCad.
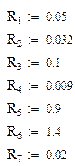
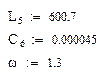

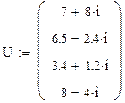
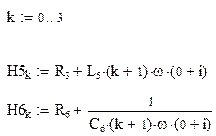
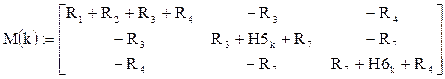
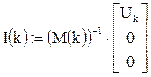
Строим графики для напряжения питания, проходящего через индуктивность тока и падения напряжения на сопротивлении 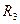
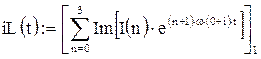
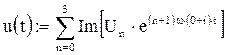
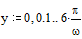

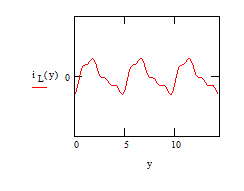
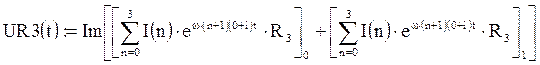
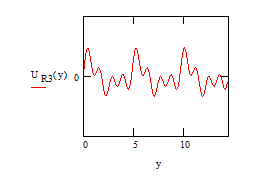
Потребляемая мощность при периодическом токе равна сумме потребляемых мощностей каждой гармонической составляющей. В свою очередь, потребляемая мощность гармонической составляющей равна 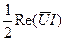 где
где 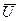 - величина, комплексно сопряженная комплексной амплитуде напряжения источника питания, а
- величина, комплексно сопряженная комплексной амплитуде напряжения источника питания, а 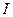 - комплексная амплитуда тока проходящего. В результате вычисления при помощи MathCad имеем:
- комплексная амплитуда тока проходящего. В результате вычисления при помощи MathCad имеем:
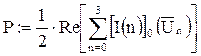
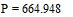
Дата добавления: 2015-09-25; просмотров: 1006;
