ПОСТОЯННОГО ТОКА
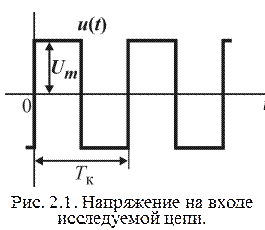 Исследование переходных процессов в данной работе проводится при подключении электрической цепи к источнику постоянного напряжения, скачкообразно изменяющегося от
Исследование переходных процессов в данной работе проводится при подключении электрической цепи к источнику постоянного напряжения, скачкообразно изменяющегося от 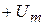 до
до 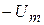 с периодом коммутации
с периодом коммутации 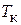 (рис. 2.1).
(рис. 2.1).
Цепи RC и RL. Электрические цепи с одним реактивным элементом называются цепями первого порядка. Простейшими примерами таких цепей являются последовательные соединения резистивного и емкостного или индуктивного элементов (рис. 2.2). При подключении цепи к источнику постоянного напряжения токи и напряжения на ее элементах будут изменяться по экспоненциальным зависимостям, приведенным в таблице 2.1.
Скачкообразное изменение входного напря-жения RC-цепи вызывает 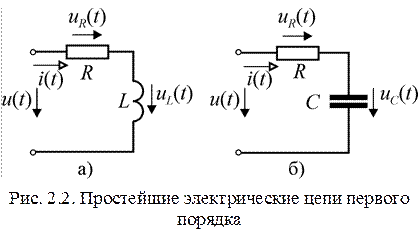 скачкообраз-ное изменение тока и напряжения на резистивном элементе с после-дующим уменьшением их до нуля по экспоненте, в то время как напряжение на емкостном элементе при скачках входного напряжения изменяется экспоненциально и непрерывно в момент коммутации.
скачкообраз-ное изменение тока и напряжения на резистивном элементе с после-дующим уменьшением их до нуля по экспоненте, в то время как напряжение на емкостном элементе при скачках входного напряжения изменяется экспоненциально и непрерывно в момент коммутации.
В RL-цепи в момент коммутации происходит скачок напряжения на индуктивном элементе, а ток и напряжение на резисторе изменяются непрерывно.
Постоянная времени экспоненты переходного процесса t является важнейшим параметром, определяющим длительность переходного процесса, а также скорость изменения тока в цепи и напряжений на ее элементах. Экспериментально ее можно определить по любой точке с известным уровнем сигнала. Относительные уровни экспоненциальных сигналов вида 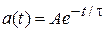 и
и 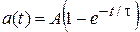 равны соответственно
равны соответственно
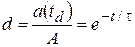 и
и 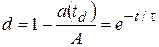 (2.1)
(2.1)
где 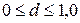 – относительный уровень сигнала в момент времени
– относительный уровень сигнала в момент времени 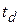 . Отсюда можно определить значение t, например, по времени
. Отсюда можно определить значение t, например, по времени 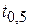 , т.е. по времени когда ток или напряжение на любом элементе цепи достигают половины своего амплитудного значения
, т.е. по времени когда ток или напряжение на любом элементе цепи достигают половины своего амплитудного значения
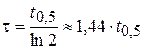 (2.2)
(2.2)
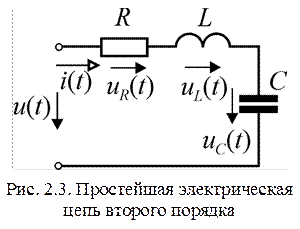 Цепь RLC. Простейшей электрической цепью второго порядка является последовательное соединение резистивного, индуктивного и емкостного элементов (рис. 2.3). Переходные функции тока и напряжений на элементах цепи (см. таблицу 2.2) могут иметь апериодический или колебательный характер, т.е. эти функции могут иметь один или несколько экстремумов. Математически тип переходного процесса полностью определяется корнями характеристического уравнения
Цепь RLC. Простейшей электрической цепью второго порядка является последовательное соединение резистивного, индуктивного и емкостного элементов (рис. 2.3). Переходные функции тока и напряжений на элементах цепи (см. таблицу 2.2) могут иметь апериодический или колебательный характер, т.е. эти функции могут иметь один или несколько экстремумов. Математически тип переходного процесса полностью определяется корнями характеристического уравнения 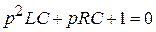 , которые зависят от соотношения параметров R, L и C. Изменить характер процесса можно вариацией любого из этих параметров или их сочетаний, однако проще всего это сделать изменением резистивного сопротивления R.
, которые зависят от соотношения параметров R, L и C. Изменить характер процесса можно вариацией любого из этих параметров или их сочетаний, однако проще всего это сделать изменением резистивного сопротивления R.
При апериодическом процессе переходные функции представляют собой сумму двух экспонент с постоянными времени
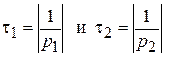 ,
,
причём 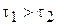 . Пренебрегая влиянием быстро затухающей экспоненты, длительность переходного процесса с достаточной точностью можно определить по первому корню характеристического уравнения:
. Пренебрегая влиянием быстро затухающей экспоненты, длительность переходного процесса с достаточной точностью можно определить по первому корню характеристического уравнения:
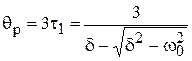 , (2.3)
, (2.3)
где – 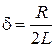 ,
, 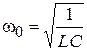 .
.
Пользуясь выражениями (2.1), можно экспериментально определить эту длительность по времени нарастания напряжения на конденсаторе до значения равного 0,9 от установившегося значения – 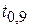 как
как
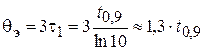 . (2.4)
. (2.4)
При колебательном процессе затухание d и частоту свободных колебаний w можно определить расчетным путем как
Таблица 2.1
| Переходные функции | Начальные и установившиеся значения | ||
| RC | 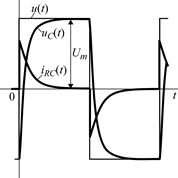
| 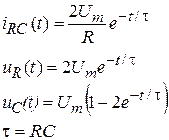
| 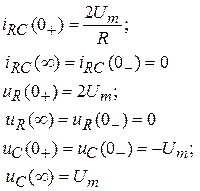
|
| RL | 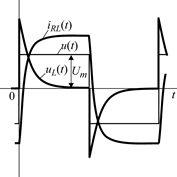
| 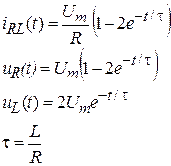
| 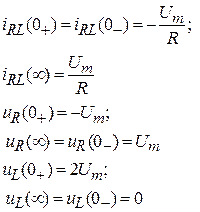
|
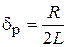 и
и 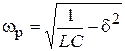 . (2.5)
. (2.5)
Экспериментально эти параметры определяются по двум соседним амплиту-дам колебаний тока 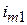 ,
, 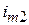 и периоду колебаний T:
и периоду колебаний T:
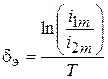 и
и 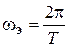 . (2.6)
. (2.6)
Таблица 2.2.
| Переходные функции | Начальные и установившиеся значения | ||
| Апериодический процесс | 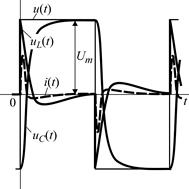
| 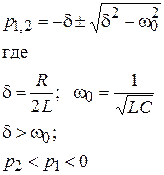
| 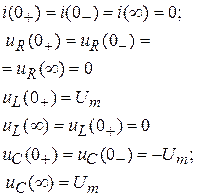
|
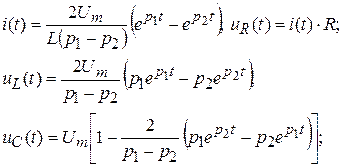
| |||
| Колебательный процесс | 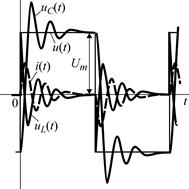
| 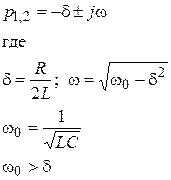
| |
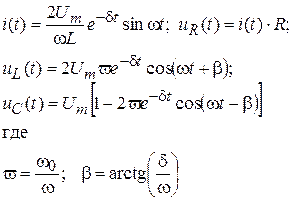
|
Дата добавления: 2015-09-23; просмотров: 956;
