Приклад. Визначимо реакції у в’язях на схемі показаної на рис.11,а.
Визначимо реакції у в’язях на схемі показаної на рис.11,а.
1) Використовуючи метод перерізів дію в’язей на схемі замінюємо дією реакцій, що можуть в них виникати. В шарнірно нерухомій опорі (т.А) можуть виникати горизонтальна ( 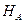 ) та вертикальна (
) та вертикальна ( 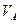 ) реакції. В опорному стержні, що з’єднується із тілом в т.В, виникає одна реакція
) реакції. В опорному стержні, що з’єднується із тілом в т.В, виникає одна реакція 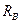 лінія дії якої проходить вздовж лініі стержня. Напрямки цих реакцій невідомі. Тому на початку задачі напрямок кожної реакції задаємо довільним чином. В результаті на вихідну схему діє система зовнішніх сил, яка складається з безпосередньо діючих на нього навантажень ( q, F, пари сил P) і реакцій відкинутих в’язей (
лінія дії якої проходить вздовж лініі стержня. Напрямки цих реакцій невідомі. Тому на початку задачі напрямок кожної реакції задаємо довільним чином. В результаті на вихідну схему діє система зовнішніх сил, яка складається з безпосередньо діючих на нього навантажень ( q, F, пари сил P) і реакцій відкинутих в’язей ( 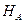 ,
, 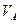 ,
, 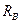 ) (рис.11,б).
) (рис.11,б).
2) Для подальших розрахунків замінимо дію рівномірно розподіленого навантаження, рівнодіючою силою 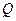 , а дію похилих сил
, а дію похилих сил 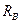 та F - їх проекціями на вісі декартової системи координат (рис.12,а):
та F - їх проекціями на вісі декартової системи координат (рис.12,а):
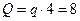 кН,
кН, 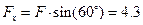 кН,
кН, 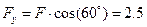 кН.
кН.
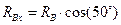 ,
, 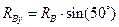
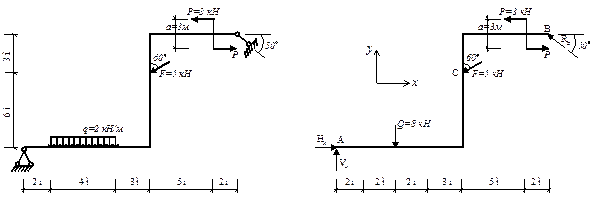
а) б)
Рис.11
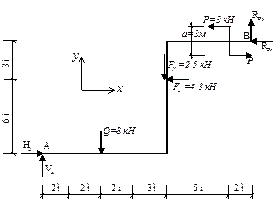
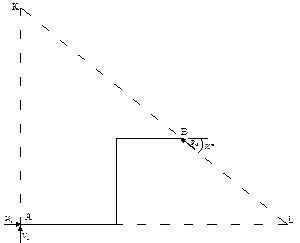 а) б)
а) б)
Рис.12
Визначення невідомих реакцій будемо виконувати виходячи з умов рівноваги які можна скласти для отриманої системи сил. Спочатку візьмемо суму проекцій всіх сил на вісі x та y декартової системи координат:
1. 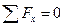
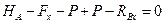
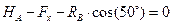
2. 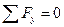
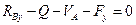
На основі отриманих рівнянь визначити реакції неможливо, оскільки в кожному з них по дві невідомих.
При складанні третього рівняння необхідно вибрати таку точку на площині, відносно якої лише одна з трьох невідомих реакцій ( 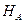 ,
, 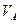 ,
, 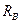 ) давала б момент. Для цього необхідно провести лініі дії всіх невідомих трьох реакцій і визначити точки в яких хоча б дві з них перетиналися (рис.12,б) В даній задачі таких точок є три (т.А,К,L). Зручніше з них взяти т.А оскільки її розташування на площині є відомим. Таким чином маємо рівняння з одним невідомим
) давала б момент. Для цього необхідно провести лініі дії всіх невідомих трьох реакцій і визначити точки в яких хоча б дві з них перетиналися (рис.12,б) В даній задачі таких точок є три (т.А,К,L). Зручніше з них взяти т.А оскільки її розташування на площині є відомим. Таким чином маємо рівняння з одним невідомим 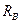 .
.
3. 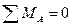 :
:
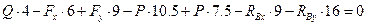
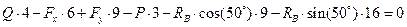
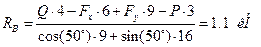
Визначивши 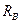 повертаємось до перших двох рівнянь і визначаємо
повертаємось до перших двох рівнянь і визначаємо 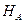 та
та 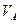 :
:
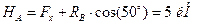 ,
,
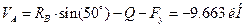 .
.
4) Після знаходження реакцій обов’язково необхідно виконати перевірку проведених розрахунків. Для цього необхідно додатково скласти ще одне рівняння рівноваги, незалежне від попередніх. Таким рівнянням може бути сума моментів всіх сил відносно будь-якої точки на площині, відносно якої знайдені реакції будуть давати ненульовий момент. Як можна побачити з рис.12,б це може бути будь-яка точка, що не розташована на лініях дії реакцій. Для виконання перевірки візьмемо суму моментів відносно точки прикладання зосередженої сили F (т.С). Оскільки система повинна знаходитись в рівновазі, в результаті маємо отримати нуль.
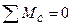
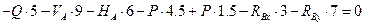
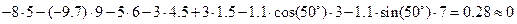
5) Після виконання перевірки встановлюємо дійсний напрямок обчислених реакцій. Якщо значення реакції вийшло додатним, то це означає що дійсний напрямок реакції співпадає з прийнятим на початку задачі. Якщо від’ємним – то дійсний напрямок є протилежним до прийнятого на початку задачі.
Як можна побачити з 1 та 2 рівнянь рівноваги пара сил не дає проекцій на вісі. ЇЇ дія виражається лише моментом 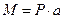 в 3 рівнянні. Тому в подальшому при розв’язанні інших задач пару сил будемо прикладати у вигляді момента, який відповідно не дає проекцій на вісі.
в 3 рівнянні. Тому в подальшому при розв’язанні інших задач пару сил будемо прикладати у вигляді момента, який відповідно не дає проекцій на вісі.
Дата добавления: 2015-09-21; просмотров: 807;
