Свойства малых частиц

Фундаментальную роль в термодинамике дисперсных систем и малых частиц играет понятие поверхностного натяжения, как фактор интенсивности поверхностной энергий. Это связано с достаточно большой долей поверхности по отношению к объему для малых частиц, т.е. удельной поверхностью.

Удельная поверхность тела a определяется отношением площади поверхности тела S к его объему:

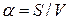. (1)

Для дисперсных систем общая поверхность всех частиц равна 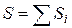- сумма площадей поверхностей всех частиц в данной системе, V – объем всей дисперсной системы.

Монодисперсные системы состоят из одинаковых по размеру частиц, а полидисперсные из неодинаковых.

Для п одинаковых частиц ,

тогда 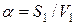, (2)

т.е. дисперсность системы можно определить и по одной частице.

S₁, V₁ - площадь поверхности и объем одной частицы.

Примеры: Для частицы кубической формы со стороной а

a= S₁ / V₁ = 6a² / a³ = 6a.

Для сферической частицы диаметром d .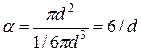

В общем случае 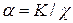, (3)

1/c = D – есть дисперсность - величина, обратно пропорциональная размеру частиц, К - коэффициент формы тела

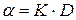. (4)

Зная массу частицы m = rV, удельную поверхность a можно определить по формуле 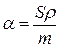, (5)

где r - плотность тела.

Другой характеристикой дисперсности является кривизна поверхности Н:

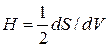. (6)

Пример: для сферы S = 4p r²; dS = 8p r

V = 4/3 p r³; dV = 4p r² ; H = 1/r.

Зависимость a от степени измельчения дана в следующей таблице

Поверхностная энергия W_n связана с коэффициентом поверхностного натяжения s W_n = sdS. (7)

Зависимость s от размера частиц имеет вид

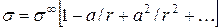. (8)

При r*®¥ имеемплоскую поверхность, тогда s®s^¥, где s^¥ - поверхностное натяжение плоской границы.

При r ® а (где а параметр решетки или межатомное расстояние) s ® 0.

Давления, возникающие в малой частице, соответствуют уравнениюЛапласа 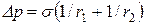. (9)

Для сферической капли r₁ = r₂ = r.

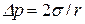, (10)

где 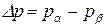- поверхностное межфазное давление,

p_a - давление внутри частицы,

p_b - давление окружающей среды.

При кристаллизации из пара, давление пара p_r над частицей радиусом r определяется по формуле Кельвина

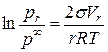, (11)

где V_r - размер кристалла, p^¥ - давление пара над плоской поверхностью,

R – газовая постоянная, Т – температура.

При кристаллизации из раствора имеет место следующая формула

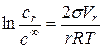, (12)

где c_r, c^¥ - концентрации выпадающей фазы на поверхности частицы и на плоской границе.

Из условия равенства химических потенциалов двух фаз с помощью формулы Кельвина (24.10) Томсон получил зависимость температуры плавления частиц T_L от их размера:

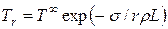, (13)

где r - плотность частицы, s - межфазная энергия , L - теплота плавления, Т^¥ - температура плавления массивного материала.

К дисперсным частицам следует отнести и кристаллические зародыши новой фазы, выпадающие из пара, раствора, расплава, аморфной среды, при твердофазных превращениях.

Изменение свободной энергии Гиббса 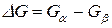сосуществующих a и b фаз состоит из объемной 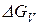и поверхностной 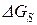составляющих

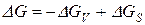, (14)

где ,

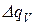– удельная объемная энергия Гиббса, V – объем тела, s - поверхностное натяжение, S – площадь поверхности частицы.

Для сферического зародыша 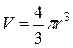, 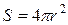. При выпадении из, например, расплава 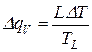, где T_L – температура плавления, DТ = T_L – Т – переохлаждение.

Тогда 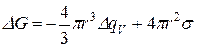. (14а)

Из условия равновесия 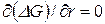находим критический размер зародыша

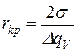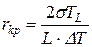или (15)

При подстановке r_кр из (24.15) в (24.14а) получим работу A_k образования зародыша

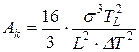. (16)

Скорость 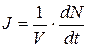образования зародышей равна

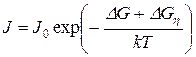, (17)

где k – постоянная Больцмана, DG – энергия активации самодиффузии, J₀ = Const.