ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ ГАЗОВ
Изменение состояния тела при взаимодействии его с окружающей средой называется термодинамическим процессом. В общем случае термодинамическом процессе могут изменяться все параметры состояния. В технической термодинамике рассматриваются следующие основные процессы:
изохорный - при постоянном объеме (V=const);
изобарный - при постоянном давлении (р =const);
изотермический - при постоянной температуре (Т=const);
адиабатный - без теплообмена (q=const);
политропный- ( 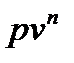 =const);
=const);
где n - показатель политропы.
Изменение внутренней энергии в термодинамических процессах с идеальным газом:
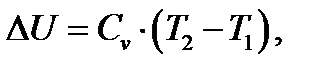 4.1
4.1
Изменение энтальпии в любом термодинамическом процессе с идеальным газом:
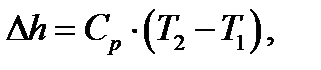 4.2
4.2
Изохорный процесс. Зависимость между основными параметрами состояния подчиняется закону Шарля
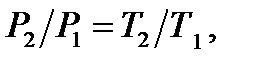 4.3
4.3
В изохорном процессе газ работу не совершает, и вся теплота идет на изменение внутренней энергии.
Изобарный процесс. Зависимость между основными параметрами состояния выражается уравнением закона Гей-Люссака
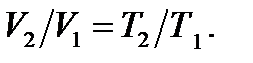 4.4
4.4
Работа изменения объема 1кг газа
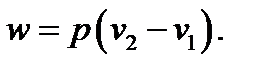 4.5
4.5
Или
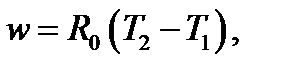 4.6
4.6
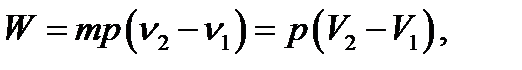 Для любой массы газа
Для любой массы газа
4.7
или
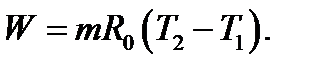 4.8
4.8
Количество теплоты процесса
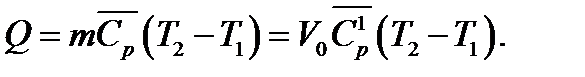 4.9
4.9
гдеV0-объем газа при нормальных физических условиях.
Зависимость между основными параметрами выражается уравнением Бойля-Мариотта:
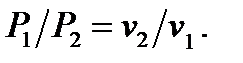 4.10
4.10
Работа единицы массы идеального газа определяется по уравнениям:
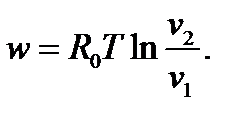 4.11
4.11
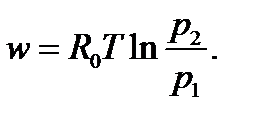 4.12
4.12
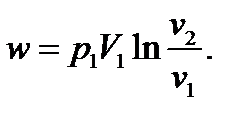 4.13
4.13
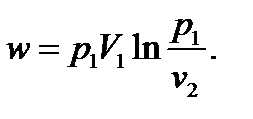 4.14
4.14
Работа совершенная m кг газа равно
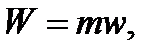 4.15
4.15
В изотермическом процессе изменение внутренней энергии равно нулю, поэтому
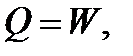 4.16
4.16
Адиабатный процесс. Уравнение процесса 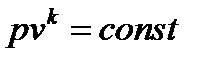 , где
, где 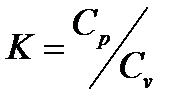 -показатель адиабаты. Зависимость между основными параметрами
-показатель адиабаты. Зависимость между основными параметрами
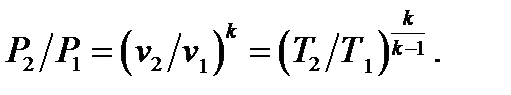 4.17
4.17
Работа единицы массы рабочего тела:
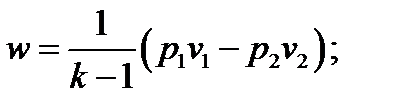 4.18
4.18
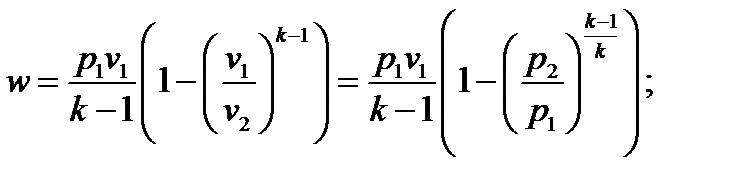 4.19
4.19
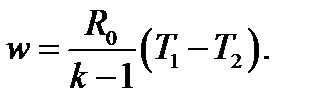 4.20
4.20
Работа любой массы газа:
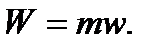 4.22
4.22
В адиабатном процессе 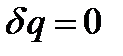 и уравнение: первого, закона термодинамики
и уравнение: первого, закона термодинамики
принимает вид 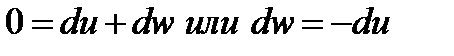 , т.е. работа в адиабатном процессе совершается за счет уменьшения внутренней энергии.
, т.е. работа в адиабатном процессе совершается за счет уменьшения внутренней энергии.
Политропный процесс. Уравнение политропы, 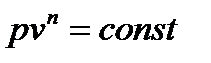 , где
, где 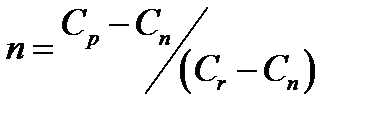 -показатель политропы. Показатель политропы может меняться от
-показатель политропы. Показатель политропы может меняться от 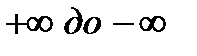 .
.
Характеристикой политропного процесса является величина
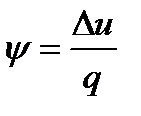 4.23
4.23
Которая может быть определена из выражения
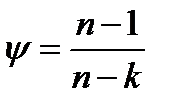 4.24
4.24
Зависимость между основными параметрами состояния, работа изменения объема газа определяется по формулам, аналогично 4.17… 4.21, но вместо показателя адиабаты применяется показатель политропы.
Количество теплоты политропного процесса:
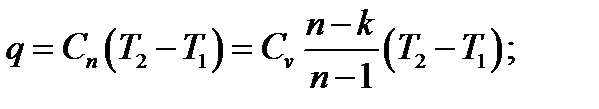 4.25
4.25
 4.26
4.26
Задачи к разделу 4
Задача 4.1. В закрытомпомещении, объемом V=150 мэ находится воздух при давленииР=100 кПа и температуре t1=5 °С. Через некоторое время, температура воздуха повышается до 30°С. Определить, какое количество теплоты сообщено воздуху, изменение внутренней энергии, и энтальпии воздуха, его конечное давление.
Решение. Нагревание воздуха протекает при постоянном, объеме, т.е. процесс изохорный. Из уравнения 4.3. Определяем конечное давление
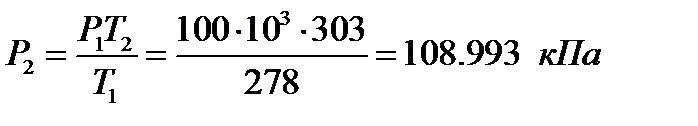
В связи с тем, что температура повышается незначительно, теплоемкость воздуха можно считать постоянной .
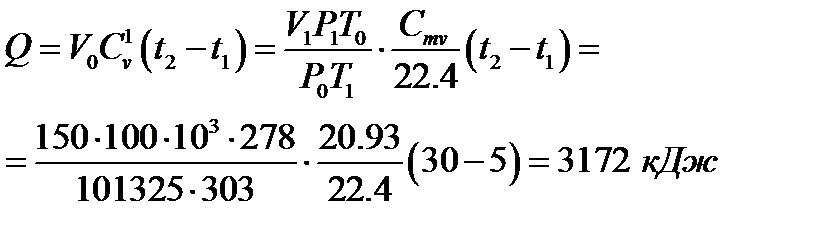
Задача 4.2. При изобарном расширении углекислого газа температура его уменьшилась от 300 до 50°С. Определить доли теплоты, затраченной на изменение внутренней энергий и на совершение работы.
Решение: В изобарном процессе подведенная теплота расходуется на изменение внутренней энергии и на совершение работы, и уравнение первого закона термодинамики принимает вид:
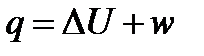
Чтобы определить, доли теплоты на изменение внутренней энергии и на совершение работы разделим данное уравнение на q
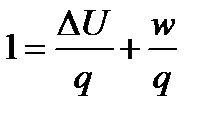
Величина 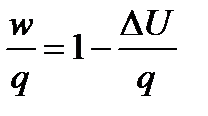 определяет ту долю всей теплоты, которая превращается в работу расширения.
определяет ту долю всей теплоты, которая превращается в работу расширения.
Так для С02 при изобарном процессе
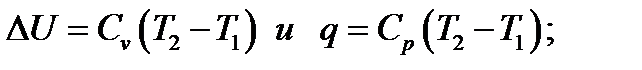
То 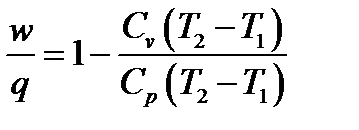
Принимая К=1,29 для С02, получаем 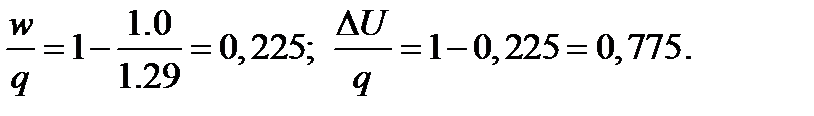
Следовательно, в изобарном процессе 22,5% теплоты превращается в работу, а 77,5 %расходуется на изменение внутренней энергии.
Задача 4.3 В охлаждаемом компрессоре изотермно сжимается V0=60 м3/ч воздуха до давления 0.6 МПа, определить затраченную мощность на сжатие и часовой расход охлаждающей воды mt компрессора, если вода нагревается при этом на10°С.
Решение. Определяем мощность, затраченной на сжатие 60 м3/ воздух. Для изотермного сжатия
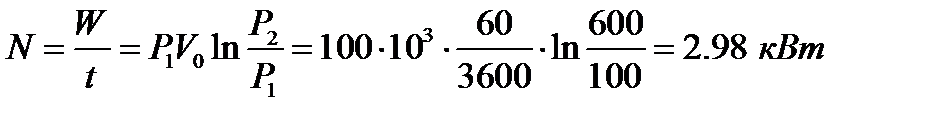
В изотермическом процессе вся затраченная работа на сжатие превращается в теплоту, которая отводится охлаждающей водой
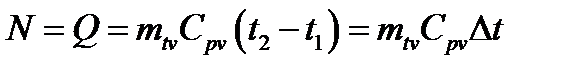 , тогда
, тогда 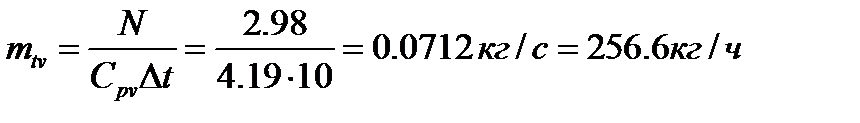
Задача 4.4.При нормальной, работе топливной аппаратуры двигателя температура смеси газов в цилиндре достигает 1900 К. После огорания, следует политропическое расширение с показателем 1.3. Объем газов при этом до открытия выпускного клапана увеличивается в 12 раз. Насколько повышается температура газов, в момент открытия выпускного клапана, если в результате ухудшения работы топливной аппаратуры при расширении топливо догорает, благодаря чему значение показателя политропы расширения становится равным 1.2. Состояние газов до расширения в обоих случаях считать одинаковым.
Решение. Из соотношения параметров политропного процесса с показателями политропы n=1,3 и n=1,2 определяем конечные температуры в конце расширения
По условию задачи 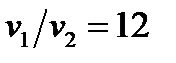 .Тогда
.Тогда 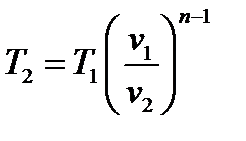
Если расширение происходит с показателем политропы n=1.3, то
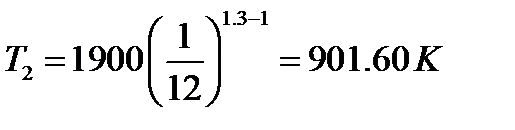 , если n=1.2 , то
, если n=1.2 , то
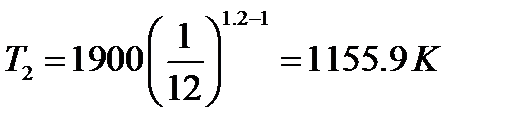
Задача 4.5 Компрессор, производительностью 120 м3/ч воздуха всасывает с давлением Р1=100 кПа, и сжимает его до давления Р2=0.7 МПа по политропе с показателем n=1.25. Вычислить, на сколько изменится работа сжатия , если сжатие будет происходить по изотерме. Температура окружающей среды 200С.
Задача 4.6 В процессе политропного расширения воздуху сообщается 80 кДж теплоты. Определить изменение внутренней энергии воздуха и производственную работу, если объем воздуха увеличился в 10 раз, а давление его уменьшилось в 8 раз.
Задача 4.72 м3 кислорода расширяется политропно от р1=0.5 МПа и t1=400C до р2=0.15 МПа. Объем занимаемый при этом воздухом, становится равным 10 м3 . Определить показатель политропы, конечную температуру, работу и теплоту процесса.
Задача 4.8Углекислый газ массой 1 кг, с начальной температурой t1=20°С и давлениемр1=1.0МПа адиабатно расширяется до давления р2=0.2МПа. Определить конечные температуру, удельный объем и работу расширения.
Задача 4.9. Кислороду в количестве 0,5 м3 при р1 =0,8 МПа и t=40°С. сообщается изотермически 65,45 кДж теплоты. Определить конечные давление и объем.
Дата добавления: 2015-09-18; просмотров: 4511;
