МЕХАНИЧЕСКИЕ СВОЙСТВА
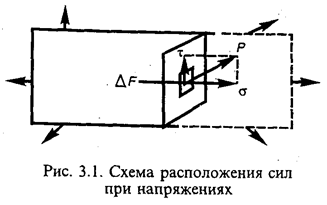
Механические свойства выражают способность материала сопротивляться напряжениям силовым (от механических нагрузок), тепловым, усадочным или другим без нарушения установившейся структуры. Чаще всего напряжение обусловлено внутренней механической силой, а его числовая величина определяется как отношение силы к единице площади. Под внутренней подразумевают силу действия частиц, находящихся по одну сторону площадки, на частицы, находящиеся по другую сторону этой площадки (рис. 3.1). Расчетом определяют нормальные (перпендикулярные к площадке) и касательные напряжения, выражаемые в размерности «сила/площадь» (МПа).
Механические свойства разделяются на деформационные и прочностные.
Деформационные свойства характеризуют способность материала к изменению формы или размеров без отклонений в величине его массы. Главнейшие виды деформаций — растяжение, сжатие, сдвиг, кручение и изгиб. Все они могут быть обратимыми и необратимыми. Обратимые полностью исчезают при прекращении действия на материал факторов, их вызвавших. Необратимые деформации, или остаточные, называемые также пластическими, накапливаются в период действия этих факторов; после их снятия деформации сохраняются. Обратимые деформации, исчезающие мгновенно и полностью, называются упругими; исчезающие в течение некоторого времени — эластическими.
Деформации могут быть также сложными — упруго-пластическими или упруго-вязко-пластическими, если достаточно четко выражены соответственно упругая и пластическая или упругая, эластическая и пластическая части (рис. 3.2).
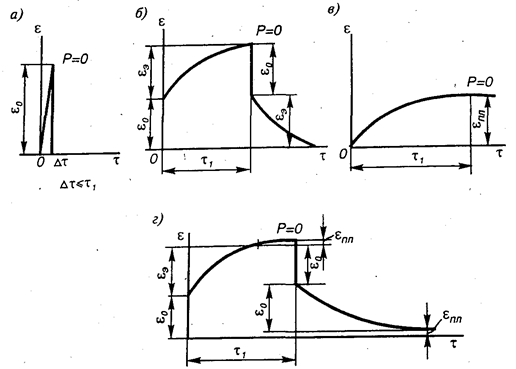
Рис. 3.2. Графики зависимости деформаций (ε) от времени (τ) действия нагрузок:
а — упругая деформация; б — упругоэластическая деформация; в — пластическая деформация; г — упругопластическая деформация
На характер и величину деформации влияют не только величина механического нагружения, но и скорость приложения этой нагрузки, а также температура материала. Как правило, с повышением скорости нагружения, а следовательно, деформирования, а также с понижением температуры материала деформации по своему характеру приближаются к упругим и упруго-пластическим, уменьшаясь по своей абсолютной величине.
Пластические деформации, медленно нарастающие без увеличения напряжения, характеризуют текучесть материала. Пластическая деформация, медленно нарастающая в течение длительного времени под влиянием силовых факторов, не способных вызвать остаточную деформацию за обычные периоды наблюдений, называется деформацией ползучести, а процесс такого деформирования — ползучестью, или крипом.
Явление ползучести выражается в непрекращающемся изменении размера тела (образца) под влиянием 'растягивающих или сжимающих силовых воздействий (напряжений ниже предела прочности) при постоянной температуре (ниже .температуры плавления). Ее обычно выражают в единицах скорости деформации, т. е. как относительное изменение размеров образца (в мм) за время (в ч): τ= (∆l/l)∙(1/ τ), где ∆l — линейное изменение образца, мм, за время τ, ч; l — начальная длина, мм.
Деформационные свойства строительных материалов, как и других тел, обусловливаются периодом, или временем релаксации. Релаксацией называется процесс самопроизвольного падения внутренних напряжений в материале, связанных с молекулярным перемещением при условии, что начальная величина деформации остается неизменной, например зафиксированной жесткими связями. Характер начальной деформации в период релаксации напряжений может измениться, например, из упругой постепенно перейти в необратимую (пластическую), что связано с переориентацией внутримолекулярной структуры. Время, или период, релаксации определяет продолжительность релаксационных процессов, в результате которых первоначальная величина напряжений при строго зафиксированной деформации снизилась в е раз (е — основание неперовых логарифмов, равное 2,718...). Так, например, если у материала в виде образца напряжение было равно 5,0 МПа, а возникшая деформация под влиянием этого напряжения была жестко зафиксирована, то время (θ с), за которое напряжение самопроизвольно снизилось до величины 5,0:2,718 = 1,85 МПа, называется временем, или периодом, релаксации, выражаемым в секундах или минутах. Эта величина — важная характеристика строительных материалов: чем она меньше, тем более деформативным является материал. Нередко время релаксации зависит от температуры материалов в момент испытания и скорости приложения нагрузки, являясь непостоянной величиной.
При весьма малой продолжительности (τ с) действия сил (или кратковременном наблюдении) по сравнению с величиной времени релаксации (τ << 6) все материалы (тела) ведут себя как упругохруп-кие тела и имеют полную обратимость деформаций, если, конечно, напряжения не нарушают их сплошности. Однако наиболее типичным случаем деформации хрупких тел (материалов) является отсутствие структурных изменений, а упругая энергия, затрачиваемая на деформацию, не успевает рассеиваться под влиянием релаксационных процессов. У упругохрупких тел возможно накопление малой упругой энергии, а за счет местных разрушений структуры происходит частичная релаксация напряжений. Приближенным значением меры хрупкости служит ψ = εy/εпред и при ψ = 1—0,8 разрушение от нагружения происходит без торможения трещин, внезапно.
При очень длительных (τ >> 9) наблюдениях за действием нагрузки (по сравнению с временем релаксации) материал подобно жидкости течет. При очень коротких наблюдениях (по сравнению с временем релаксации) даже жидкий материал проявляет хрупкость твердого кристаллического тела. Так, например, при весьма коротком времени действия силы на воду, время релаксации которой равно порядка 10-11 с, она ведет себя как кристаллическое твердое тело; при весьма длительном периоде действия сил (или наблюдения) природный камень в виде горных пород, время релаксации которого равно 1010 с, ведет себя как текучая жидкость. Но эти крайние условия не встречаются в практике строительства и эксплуатации конструкций зданий и сооружений, поэтому вода всегда кажется жидкой, а камень — твердым. Однако многие материалы остаются весьма чувствительными к различию между временем действия нагрузки и временем релаксации, особенно при повышенных температурах, когда процесс релаксации напряжений в некоторых материалах заметно интенсифицируется, особенно при местных (локальных) перенапряжениях в материале.
Кроме времени релаксации, в расчетах пользуются коэффициентом у релаксации, показывающим долю спада напряжений за определенный период времени: ψ = στ/σ0, где στ — напряжение в момент времени τ при постоянной деформации; σ0 — начальное напряжение.
Коэффициент релаксации позволяет расчетным путем определить релаксационную характеристику с помощью опытных значений деформации ползучести, точнее —скорости ползучести, получаемых менее трудоемким измерением, чем релаксации напряжений. С некоторым приближением к опытным данным можно воспользоваться зависимостью: ln ψ = -φ , где φ — коэффициент ползучести, равный ετ/ε0 = Е0/εS; ετ — деформация ползучести в момент времени τ при постоянном напряжении σ0; ε0 — начальная упругая деформация, равная σ0/Е0; Е0 — начальный модуль упругости, равный σ0/ ε0; εS — удельная деформация ползучести в момент времени τ, равная ετ/σ0.
Прочность характеризует способность материала в определенных условиях и пределах, не разрушаясь, сопротивляться внутренним напряжениям и деформациям, возникающим под влиянием механических, тепловых и других напряжений.
Типичными прочностными характеристиками служат предел упругости, предел текучести и предел прочности при воздействии
сжимающих, растягивающих или других видов усилий. Пределу упругости соответствует напряжение материала при максимальной величине упругой деформации; пределу текучести — постоянное напряжение при нарастании пластической деформации; пределу прочности — максимальное напряжение в момент разрушения материала (рис. 3.3). Эти характеристики прочности относятся к кратковременному действию приложенной нагрузки (табл. 3.1). При длительном действии нагрузки возрастает опасность нарушения структуры материала. Даже сравнительно малые величины напряжения (например, от собственной массы) могут вызвать ползучесть и заметное ухудшение структуры с потерей прочности. Нередко измеряют длительную прочность материала не только при статической (неподвижной), но и динамической нагрузках. Материал может резко терять свою прочность после приложения к нему вибрационной нагрузки, что обусловлено усталостью — накоплением неотрелаксированных напряжений и необратимых микродефектов в структуре. Соответствующая прочность материала называется усталостной и определяется специальным испытанием образцов.
Таблица 3.1. Физико-механическиесвойства некоторых материалов
| Наименование материала | Предел прочности при сжатии, МПа | Истинная плотность, кг/м3 | Средняя плотность, кг/м3 | Теплопроводность, Вт/(м-°С) |
| Гранит | 150—250 | 2600—2800 | 2500—2700 | 2,9-3,3 |
| Известняк плотный | 50—150 | 2400—2600 | 1800—2200 | 0,8—1,0 |
| Известняк-ракушечник | 0,5—5 | 2300—2400 | 900—1400 | 0,3—0,6 |
| Кирпич керамический | 10—20 | 2600—2700 | 1700—2000 | 0,8—0,9 |
| Кирпич силикатный | 10—20 | 2400—2550 | 1700—1900 | — |
| Бетон тяжелый | 10—60 | 2500—2600 | 1800—2500 | 1,1—1,6 |
| Бетон легкий | 2—15 | — | 500—1800 | 0,35—0,8 |
| Древесина сосновая | 30—60 | 1550-1600 | 500—600 | 0,15—0,2 |
| Сталь Ст.З (при растя-жен.) | 380-450 | 7800—7900 | 7800—7900 | 58 |
| Пластмассы | 120—200 | 1000—2200 | 100—1200 | 0,23—0,80 |
| Портландцемент, ,кг/см2 (марка) | 300—600 | 3000—3200 | Насыпная плотность 1200—1300 | — |
В целом упомянутые выше характеристики прочности по своей сущности относятся к условным по двум причинам. Во-первых, они не учитывают фактора времени, что с некоторым приближением можно допустить только в отношении хрупких материалов. Во-вторых, приборы, размеры и форма образцов, скорость приложения нагрузки на прессе и другие исходные параметры методов испытания материала на прочность приняты условными. Поэтому материал может иметь различную величину показателя прочности в зависимости от размера образца, скорости приложения нагрузки и конструкции прибора, на котором испытывались образцы. Например, чем меньше размеры «кубика», больше скорость приложения нагрузки (или скорости деформации), тем выше получаемая величина предела прочности при испытании на сжатие.
В упругой области деформаций действует закон Гука: σ = Е∙ε, где σ — напряжение, МПа; ε — относительная упругая деформация; Е — модуль упругости материала, МПа. Если относительная деформация ε, выражающая отношение прироста деформации ∆l к первоначальной длине образца l, т. е. ∆l /l окажется равным единице (ε = 1), то Е = σ. Отсюда следует, что модуль упругости по своему физическому смыслу численно равен напряжению, которое потребовалось приложить к материалу (образцу), чтобы вызвать относительную деформацию ε = 1 (что возможно, когда приращение ∆l = l) , т. е. когда было удвоение длины образца при условии сохранности упругих свойств материала. В реальных строительных материалах (кроме резины) величина упругой деформации всегда гораздо меньше, составляя у стали 1—1,5 %, а у хрупких она и вовсе приближается к нулю.
Численные значения величины модуля упругости и прочности определяют как с разрушением образцов, например при испытании под прессом, так и неразрушающими (адеструктивными) методами. Распространены следующие адеструктивные методы их измерения: акустические, магнитные и электромагнитные, механические, радиометрические, рентгеновские и электрические. Они основаны на прямых и обратных закономерностях между физическими значениями, получаемыми при испытании неразрушающим прибором, и традиционными показателями свойств. Зависимости выражаются в виде формул, таблиц, тарировочных графиков. Измерения становятся более эффективными при комплексном использовании адест-руктивных методов измерения с получением двух или нескольких физических характеристик.
К комплексным методам относится совместное применение механического и ультразвукового методов или радиометрического и ультразвукового и других для определения предела прочности и модуля упругости, контроля качества и дефектоскопии, однородности по различным показателям (прочности, влажности, толщине защитного слоя и др.). Эти методы весьма эффективны при контроле за сохранением оптимальности структуры материалов и изделий по однородности, минимуму дефектов, плотности, континуальности пространственной сетки вяжущего вещества или жидкостной оболочки свежеизготовленного монолита, минимального количества вяжущего вещества или другим обязательным ее параметрам. В частности, набору параметров оптимальной структуры соответствует наиболее широкий спектр частот ультразвукового сигнала, а также наибольшая амплитудная характеристика.
Альтернативой условным методам определения прочности имеются инвариантные, независимые от обстановки опыта. К инвариантным характеристикам прочности относятся предельное напряжение сдвига (Рк), структурная вязкость и другие, определяемые с помощью построения реологических кривых по данным измерений на вискозиметрах, пластометрах и других приборах. Принцип действия таких приборов основан на истечении массы через капилляр заданного диаметра или на погружении в вещество металлического конуса, шара или других тел. При испытаниях осуществляется чистый и однородный сдвиг частиц вещества относительно друг друга в плоскостных или цилиндрических (коаксиальных) приборах (вискозиметрах) и достаточно четко устанавливается, что прочностные характеристики существенно зависят от продолжительности действия механического усилия, являются типичными кинетическими величинами.
Кроме прочности технической или реальной, определяемой с помощью условных или инвариантных приборов, существует прочность, определяемая вычислением и поэтому называемая теоретической. Простейший метод оценки теоретической прочности твердых тел был, в свое время, предложен Поляки. Так, если для разрыва стержня сечением 1 м2 потребовалось приложить напряжение сто, а атомные плоскости при этом удалились друг от друга на величину а, адекватную порядку параметра кристаллической решетки, то работа выразилась как σ0∙а. При разрыве образовались две новых поверхности площадью 2 м2, а затраченная работа перешла в свободную поверхностную энергию. Последнюю можно обозначить как g и выразить в Дж/м2. Следовательно, σ0∙а = 2%. Отсюда искомая теоретическая прочность σ0 = 2g/а.
Существуют и другие методы определения теоретической прочности хрупких твердых тел, например по теплоте сублимации (переходе вещества из твердого состояния в газообразное без превращения в жидкость); по методу Поляни—Орована (из сил молекулярного взаимодействия) и др. Установлено, что независимо от метода вычисления результаты дают близкие значения теоретической прочности для твердых тел: σ0 ≈ 0,1Е. Учитывая высокие значения модуля упругости (табл. 3.2), становится очевидным, что теоретическая прочность твердых тел и кристаллов также очень велика. Что же касается технической (реальной) прочности, то она в 100—1000 раз, т. е. на два-три десятичных порядка, ниже теоретической прочности (см. табл. 3.2). Большое различие между теоретической и реальной прочностью материалов объясняется дефектностью микроструктуры, т. е. наличием микротрещин, пор и т. п. Чем крупнее образцы твердых тел, принятых для испытания, тем больше концентрируется в них дефектов, а поэтому их реальная прочность ниже, т. е. действует обратная зависимость прочности от размера изделий (масштабного фактора).
Таблица 3.2. Свойства некоторых металлических и неметаллических материалов
| Вещество | Модуль упругости Е, 10-7 Па | Теоретическая прочность σ0, 10-7 Па | Техническая прочность στ, 10-7 Па | Отношение σ0/στ |
| Алюминий катаный | ||||
| Медь прокатная | ||||
| Железоуглеродистая сталь | ||||
| Стекло | ||||
| Дерево вдоль волокон | ||||
| Полистирол |
Наиболее обстоятельно метод расчета реальной (технической) прочности хрупких твердых тел исследовал Гриффите. Им предложена формула для расчета этой прочности материала, имеющего микротрещину:
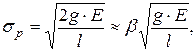 (3.1)
(3.1)
где g и Е — соответственно свободная поверхностная энергия образца и модуль упругости материала, l — длина поперечной микротрещины в образце, составляющая обычно к моменту разрушения образца несколько микрон или более; β — числовой коэффициент, зависящий от вязкости и характера материала: наличия кристаллической и аморфной фаз, их количественного соотношения, дефектов в кристаллической решетке (вакансий, дислокации), микропор в аморфной части структуры.
Следует отметить, что прочность больше, чем некоторые другие свойства материала, проявляет чувствительность к явлениям и процессам формирования и изменения структуры, особенно кристаллической. Прочность является структурно-чувствительным свойством, поэтому ее можно изменять в необходимом направлении путем соответствующих корректив структуры на микро- или макроуровне; уменьшения дефектов; введения добавок, например кристаллических затравок; повышения дисперсности новообразующихся фаз; оптимизации структуры, изменения пористости и размера пор и др.
Дополнительными характеристиками механических свойств материалов служат твердость, истираемость, ударная вязкость. Твердость выражает способность материала сопротивляться проникновению в него более твердых тел, например при испытании на склерометрах путем вдавливания стального шарика или стального конуса, царапании резцом, сверлении, ударе молотком, пулевом вы стреле и пр. Эти испытания дают условные значения твердости либо только качественные, например по следу царапания, либо также и количественные — по глубине или площади отпечатка с учетом приложенной нагрузки. Нередко стремятся перейти от полученного значения твердости к величине прочности. Устанавливаемые отношения между твердостью и прочностью тем менее точны, чем пластичнее материал. Только у хрупких тел царапание можно более или менее надежно сравнивать с прочностью, поскольку оба этих свойства обусловлены в основном сцеплением между микрочастицами материала.
Нередко о твердости судят также по потере массы образцов при истирании на металлических кругах с добавлением абразивных порошков.
Более сложным свойством, включающим прочность и твердость, служит износ. Об износостойкости материала судят по испытанию пробы определенной массы во вращающемся барабане с металлическими шарами или без шаров, в течение определенного периода времени или определенной частоты вращения. Чем больше измельчается проба, тем, следовательно, и больше ее износ (в %).
Ударная вязкость характеризует способность материала сопротивляться сосредоточенным ударным нагрузкам и определяется количеством работы, затрачиваемой на излом образца в фиксированном с помощью насечки месте. Работа, отнесенная к площади поперечника образца, характеризует единичную ударную работу на излом, называемую удельной ударной вязкостью. Она имеет практическое значение при оценке качества металлов, асбестоцементных изделий, например кровельных листов и плит.
Дата добавления: 2015-09-18; просмотров: 1125;
