Ориентированное дерево (называемое также древовидностью) определяется аналогичным образом.

Ориентированное дерево представляет собой ориентированный граф без циклов, в котором полустепень захода каждой вершины, за исключением одной (например, вершины х₁), равна единице, а полустепень захода вершины х₁(называемой корнем этого дерева) равна нулю.

На рисунке 3.8 показан граф, который является ориентированным деревом с корнем в вершине х₁. Из приведенного определения следует, что ориентированное дерево с п вершинами имеет n-1 дуг и связно. Также очевидно, что не всякий ориентированный граф содержит основное ориентированное дерево. Это подтверждает граф, изображенный на рисунке 3.9.

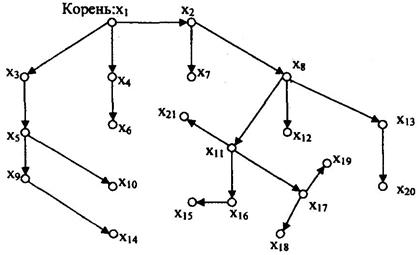
Рисунок 3.9. Ориентированное дерево

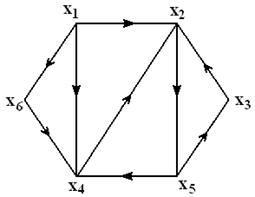
Рисунок 3.10. Граф без ориентированного основного графа

Следует отметить, что неориентированное дерево можно преобразовать в ориентированное: надо взять его произвольную вершину в качестве корня и ребрам приписать такую ориентацию, чтобы каждая вершина соединялась с корнем (только одной) простой цепью.

Обратно, если Т= (X, В) - ориентированное дерево, то Т = (X, В), где В — множество дуг дерева Т без учета их ориентации, является неориентированным деревом.

«Генеалогическое дерево», в котором вершины соответствуют лицам мужского пола, а дуги ориентированы от родителей к детям, представляет собой хорошо известный пример ориентированного дерева. Корень в этом дереве соответствует «основателю» рода (лицу, родившемуся раньше остальных).

Контрольные вопросы

1. Что называется множеством?

2. Назовите виды множества.

3. Из чего состоит множества?

4. Охарактеризуйте основные операции над множествами.

5. В каком году был создан аппарат алгебры логики и кем?

6. Что является основным понятием булевой алгебры и дайте его определение?

7. Из чего состоит аппарат булевой алгебры, как формальной математической системы?

8. Охарактеризуйте основные базовые операции булевой алгебры.

9. Какие таблицы истинности Вы знаете?

10. Дайте характеристику аксиомам алгебры логики.

11. Что называется булевой функцией?

12. Чем может быть представлена булевая функция?

13. Приведите формулы логики булевых функций.

14. Дать понятие «графу».

15. Назовите виды графов и дайте их определения.

16. Как определяется число ребер графа?

17. Дайте определения понятиям: «маршрут», «компонента связности», «путь», «цикл», «эйлеровый цикл», «гамильтовый цикл».

18. Как задается граф?

19. Что называется деревом?

20. Какие бывают деревья? Покажите их графически.

Тема 4. Основные понятия архитектуры ЭВМ